多项式曲线拟合（Polynomial Curve Fitting）

监督学习

@ author : duanxxnj@163.com
@ time : 2016-06-19

原文链接

多项式特征生成

在机器学习算法中，基于针对数据的非线性函数的线性模型是非常常见的，这种方法即可以像线性模型一样高效的运算，同时使得模型可以适用于更为广泛的数据上，多项式拟合就是这类算法中最为简单的一个。

关于多项式回归的应用，这里举个非常简单的例子:一般的线性回归，模型既是参数$w$的线性函数，同时也是输入变量$x$的线性函数，对于一个二维的数据而言，模型的数学表达式如下：

$$\tilde{y}(x,w)=w_{0} + w_{1}x_{1}+w_{2}x_{2}$$

如果想要拟合一个抛物面，而不是拟合一个平面的话，那么就需计算输入变量$x$二次项的线性组合，则模型更新为下面这个形式：

$$\tilde{y}(x,w)=w_{0} + w_{1}x_{1}+w_{2}x_{2}+w_{4}x_{1}^2+w_{5}x_{2}^2$$

注意：这里需要说明的是，更新后的模型，虽然是输入变量$x$的二次函数，但是，由于它仍然是参数$w$的一次线性函数，所以它仍然是一个线性模型。为了说明这个问题，可以假设有一个新的变量$z=[x_{1},x_{2},x_{1}x_{2},x_{1}^2,x_{2}^2]$，那么就可以将上面的模型重写为下面的这个形式：

$$\tilde{y}(x,w)=w_{0} + w_{1}z_{1}+w_{2}z_{2}+w_{3}z_{3}+w_{4}z_{4}+w_{5}z_{5}$$

用向量$z$替换向量$x$的过程，相当于一个特征变换或者叫做特征生成的过程，它将输入特征的维度提高，但模型仍然是一个线性模型。下面这个代码片段可以实现特征升维的过程，其特征变换的规则为：从$[x_{1},x_{2}]$变为 $[x_{1},x_{2},x_{1}x_{2},x_{1}^2,x_{2}^2]$。

#!/usr/bin/python
# -*- coding: utf-8 -*-
"""
author ： duanxxnj@163.com
time : 2016-06-04_14-00
多项式特征生成
"""
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
# 首先生成3x2的原始特征矩阵
# 即样本数为3，特征数为2
X = np.arange(6).reshape(3, 2)
print '原始数据：'
print X
# 特生变换/特征生成
# 将原始一阶数据升维到二阶数据
# 升维方式是： [x_1, x_2] 变为 [1, x_1, x_2, x_1^2, x_1 x_2, x_2^2]
polyFeat = PolynomialFeatures(degree=2)
X_transformed = polyFeat.fit_transform(X)
print '特征变换后的数据：'
print X_transformed

运行结果为：

原始数据：
[[0 1]
 [2 3]
 [4 5]]
特征变换后的数据：
[[  1.   0.   1.   0.   0.   1.]
 [  1.   2.   3.   4.   6.   9.]
 [  1.   4.   5.  16.  20.  25.]]

多项式拟合

在《线性回归》中就提到过多项式拟合，从本质上讲，多项式拟合也是一个线性模型，其数学表达式为：

$$y(x,w)=\sum_{j=0}^M\omega_{j}x^j$$

其中$M$是多项式的最高次数，$x^j$代表的是$x$的$j$次幂，$w_{j}$是$x^j$的系数。
样本的数目为$N$,对于每一个样本$x_{n}$，其对应的输出为$t_{n}$，用平方误差和（sum of the squares of the errors）作为损失函数，那么损失函数可以表示为：

$$E(w)=\frac{1}{2}\sum_{n=1}^N\{y(x_{n},w)-t_{n}\}^2$$

这里在损失函数前面加入一个$\frac{1}{2}$，只是为了后面的推导方便，其并不影响最终的结果。

经过上面的分析可以知道，多项式拟合其实是两个过程：
1. 对原始特征向量$x$做多项式特征生成，得到新的特征$z$
2. 对新的特征$z$做线性回归

#!/usr/bin/python
# -*- coding: utf-8 -*-
"""
author ： duanxxnj@163.com
time : 2016-06-04_16-38
这个例子展示了多项式曲线拟合的特性
多项式曲线拟合分为两个步骤：
1、根据多项式的最高次数，对输入特征向量做特征生成
    对原来的每一个特征向量而言，可以生成一个范特蒙德矩阵（ Vandermonde matrix）
    范特蒙德矩阵的尺寸为：[n_samples , n_degree+1]
    其形式为：
    [[1, x_1, x_1 ** 2, x_1 ** 3, ...],
     [1, x_2, x_2 ** 2, x_2 ** 3, ...],
     ...]
2、基于第一步生成的范特蒙德矩阵，直接使用已有线性回归模型，就可以实现多项式回归
这个例子展示了如何基于线性回归模做非线性回归，其实这个也是核函数的基本思想。
"""
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
# 多项式回归需要拟合的函数
def f(x):
    return x * np.sin(x)
# 产生绘图用的原始数据点
# 这里产生的点的范围比实际拟合所采用的点的范围要宽一些
# 其目的是为了展示当多项式拟合的次数过高时，过拟合的现象
# 过拟合的模型在训练数据范围内，拟合效果非常好
# 在训练数据范围外，模型的拟合效果特别误差
x_plot = np.linspace(-1, 13, 140)
# 训练用数据范围
x = np.linspace(0, 10, 100)
# 随机取训练数据中的10个点作为拟合用的点
rng = np.random.RandomState(0)
rng.shuffle(x)
x = np.sort(x[:10])
y = f(x)
# 将数据从行向量换为列向量，这样每一行就能代表一个样本
X = x[:, np.newaxis]
X_plot = x_plot[:, np.newaxis]
# 从次数为1一直到次数变为17，模型的次数增长步长为3
# 下面会绘制出不同的次数所对应的图像
# 需要注意的是，这6个图的坐标系的y轴的数据范围相差是非常大的
# 模型的次数越高，在训练数据外的测试点上，y的数据和原始数据相差越大
# 即：过拟合现象越明显
#
# 同时，下面还输出了不同次数下，模型对应的参数向量w
# 可以看到，模型次数越大，模型所对应的参数向量的模||w||也越大
# 即：过拟合现象越明显，模型所对应的参数向量的模||w||也越大
#
# 在损失函数后面，加上模型所对应的参数向量的模||w||
# 那么，在最小化损失函数的同时，也限制了参数向量的模||w||的增长
# 这就是正则化可以防止过拟合的原因
#
# 但是在实际测试中发现，如果随机取训练数据的时候，选取的是20个点
# 那么参数向量的模||w||并不是随着模型复杂度的增加而增加
# 这个是因为训练的样本足够大的时候，能够有效的描述原始数据分布
# 那么过拟合的这一套理论就不是特别的适用了
# 所以，方法的选择还是要建立在对数据分布充分的认识上才行
#
for degree in range(9):
    # 基于不同的次数生成多项式模型
    model = make_pipeline(PolynomialFeatures(degree), LinearRegression())
    model.fit(X, y)
    # 不同次数下，多项式模型的参数
    print '模型次数为：', degree, ' 时，模型的参数向量的模：'
    print np.dot(np.array(model.steps[1][2].coef_),
                 np.array(model.steps[1][3].coef_))
    print '模型的参数为：'
    print model.steps[1][4].coef_
    y_plot = model.predict(X_plot)
    plt.subplot('52' + str(degree + 1))
    plt.grid()
    plt.plot(x_plot, f(x_plot), label="ground truth")
    plt.scatter(x, y, label="training points")
    plt.plot(x_plot, y_plot, label="degree %d" % degree)
    plt.legend(loc='lower left')
plt.show()

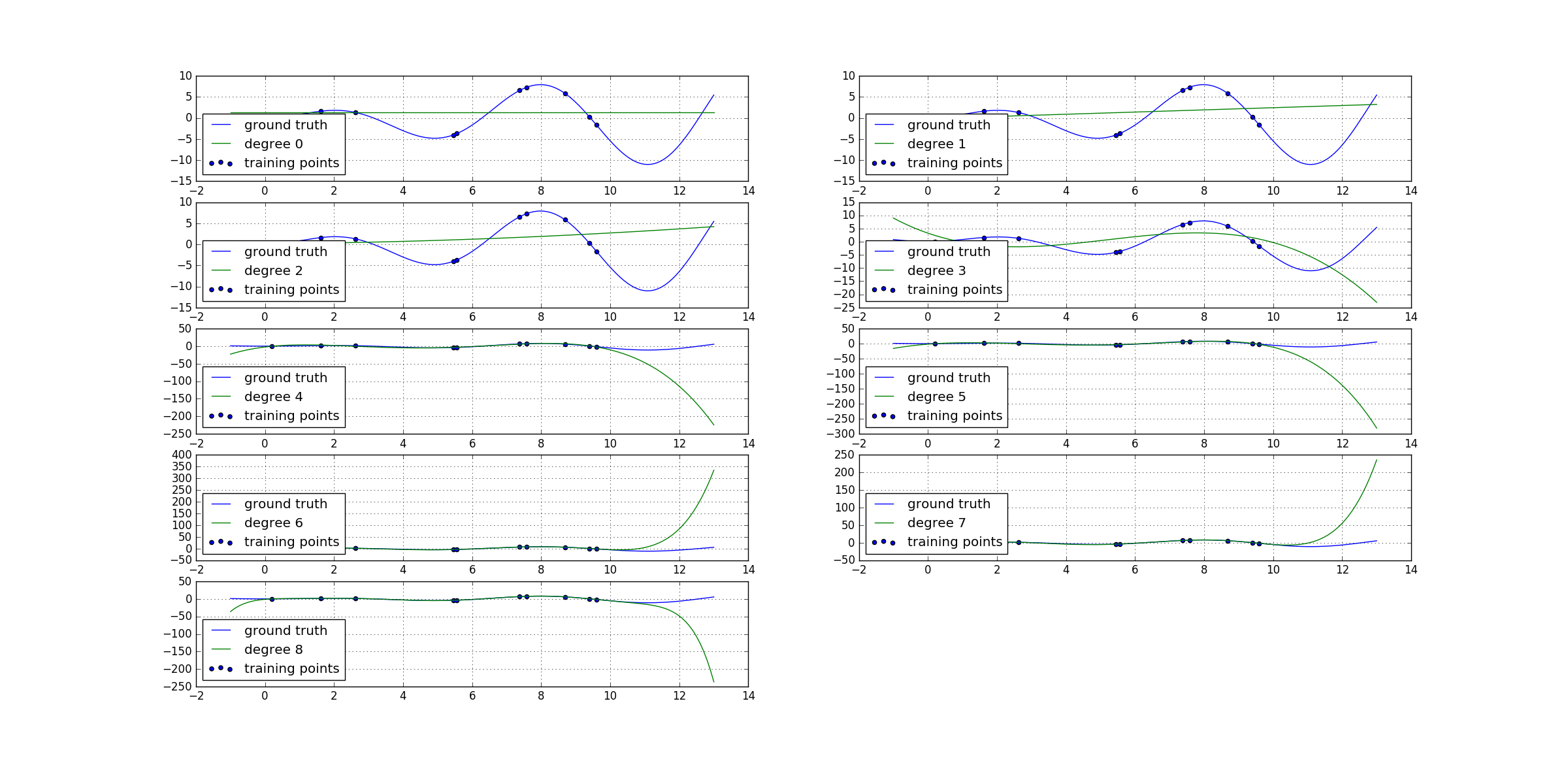
过拟合

从上面的代码的运行结果如下：

模型次数为： 0  时，模型的参数向量的模：
0.0
模型的参数为：
[ 0.]
模型次数为： 1  时，模型的参数向量的模：
0.0672247305597
模型的参数为：
[ 0.          0.25927732]
模型次数为： 2  时，模型的参数向量的模：
0.00485169982253
模型的参数为：
[ 0.          0.06702261  0.01896495]
模型次数为： 3  时，模型的参数向量的模：
21.6855657558
模型的参数为：
[ 0.         -4.50881058  1.16216004 -0.07467912]
模型次数为： 4  时，模型的参数向量的模：
193.44229814
模型的参数为：
[  0.          11.8668248   -7.13912616   1.28405087  -0.06970187]
模型次数为： 5  时，模型的参数向量的模：
100.775416362
模型的参数为：
[  0.00000000e+00   8.81727284e+00  -4.75722615e+00   6.32370347e-01
   3.81031381e-03  -2.92969155e-03]
模型次数为： 6  时，模型的参数向量的模：
412.685941253
模型的参数为：
[  0.00000000e+00  -1.12195467e+01   1.52609522e+01  -7.19720894e+00
   1.44728030e+00  -1.28827774e-01   4.18692299e-03]
模型次数为： 7  时，模型的参数向量的模：
584.784763013
模型的参数为：
[  0.00000000e+00  -1.33786428e+01   1.80697292e+01  -8.70772778e+00
   1.85005336e+00  -1.85152116e-01   8.14689351e-03  -1.10477347e-04]
模型次数为： 8  时，模型的参数向量的模：
325.113163284
模型的参数为：
[  0.00000000e+00   8.34477828e+00  -1.22270425e+01   9.49806252e+00
  -3.88031716e+00   8.35492773e-01  -9.56033297e-02   5.50928798e-03
  -1.25987578e-04]

可以明显的看出来，模型的次数越高，参数向量的模就越大，那么其拟合程度就越高，越容易产生过拟合。

注意： 在实际测试中发现，如果随机取训练数据的时候，选取的是20个点那么参数向量的模||w||并不是随着模型复杂度的增加而增加。这个是因为训练的样本足够大，能够有效的描述原始数据分布的时候，那么过拟合的这一套理论就不是特别的适用了。所以，方法的选择还是要建立在对数据分布充分的认识上才行

模型的概率解释

关于线性模型可以通过其概率意义进行解释，我个人也是最信服这种解释方式。即：真实值$t_{n}$，是输入$x_{n}$在模型$y(x,w)$上加入了一个噪声产生的，其数学表达式如下:

$$t_{n}=y(x_{n},w)+\epsilon$$

而我们一般可以定义噪声$\epsilon$为高斯分布$N(0,\sigma^2)$，那么可以很容易得到，$t$是以$y(x,w)$为均值的高斯分布：

$$p(t|x,w,\sigma^2)=N(t|y(x,w),\sigma^2)$$

那么对于训练数据$\{X,t\}$而言，可以使用极大似然估计来计算参数$w$和$\sigma^2$：

$$p(t|X,w,\sigma^2)=\prod_{n=1}^NN(t_{n}|y(x_{n},w),\sigma^2)$$

取对数似然估计：

$$lnp(t|X,w,\sigma^2)=-\frac{1}{2\sigma^2}\sum_{n=1}^N\{y(x_{n},w)-t_{n}\}^2-\frac{N}{2}ln2\pi-Nln\sigma$$

首先估计参数$w$，那么就可以略去和$w$无关的所有项。最后就是剩下下面这个式子：

$$\sum_{n=1}^N\{y(x_{n},w)-t_{n}\}^2$$

这个就是一开始使用的平方误差和（sum of the squares of the errors），这也解释为什么用平方误差和作为损失函数了，$w$的解在线性回归那一节中已经有说明。

在估计出$w_{ML}$后，再来估计参数$\sigma^2$，这里取$\beta^{-1}=\sigma^2$，则对数似然估计就变成了：

$$lnp(t|X,w,\beta)=-\frac{\beta}{2}\sum_{n=1}^N\{y(x_{n},w)-t_{n}\}^2-\frac{N}{2}ln2\pi-\frac{N}{2}ln\beta$$

对其关于$\beta$求导，就可以得到：

$$-\frac{1}{2}\sum_{n=1}^N\{y(x_{n},w)-t_{n}\}^2 - \frac{N}{2}\beta=0$$

所以可以得到：

$$\sigma_{ML}^2=\frac{1}{\beta_{ML}}=\frac{1}{N}\sum_{n=1}^N\{y(x_{n},w_{ML})-t_{n}\}^2\}$$

现在参数$w_{ML}$和$\sigma_{ML}^2$都已经估计出来了，那么我么就有了$t$关于$x$的概率分布模型：

$$p(t|x,w_{ML},\sigma_{ML}^2)=N(t|y(x,w_{ML}),\sigma_{ML}^2)$$

有了这个模型，对于输入$x$就可以很容易的得到对于的$t$，及其概率。

正则项的贝叶斯先验解释

在已经得到刚才的概率模型的前提下，这里进一步引入贝叶斯规则，可以假设，参数$w$拥有高斯先验分布：

$$p(w|\alpha)=N(w|0,\alpha^{-1}I)=(\frac{\alpha}{2\pi})^{(M+1)/2}exp\{-\frac{\alpha}{2}w^Tw\}$$

这里$M+1$是模型的复杂度，即多项式回归的次数。那么，根据贝叶斯规则：

$$p(w|X,t,\alpha,\beta)=p(t|X,w,\beta)p(w,\alpha)$$

这个叫做MAP极大后验概率(maximum posterior）。对这个式子做对数似然，去除无关项之后，可以很容易得到下面这个结果：

$$-\frac{\beta}{2}\sum_{n=1}^N\{y(x_{n},w)-t_{n}\}^2+\frac{\alpha}{2}w^Tw$$

这里可以看出，先验概率对应的就是正则项，其正则参数为$\lambda=\alpha/\beta$。

可以假设，复杂的模型有较小的先验概率，而相对简单的模型有较大的先验概率。