RNN（recurrent neural networks）循环神经网络

神经网络&深度学习

---

@author : duanxxnj@163.com
@time : 2016-11-21

---

RNN（递归神经网络）在NLP中的应用已经非常的广泛，但是关于RNN具体实现及工作方式的文章却比价的少，这里我首先介绍受RNN的原理，然后使用Python语言实现一个RNN。

RNN简介

要详细的说明RNN，首先就需要参考一篇最为原始的论文《Finding Structure in Time》，这是JEFFREY L. ELMAN 1990年的一篇论文。这篇论文主要论述的是如何在时间序列中找到一个特定的模式（pattern）或者结构（structure），几乎就是这篇论文提出了RNN最初的概念框架。

对于具有时序性的数据（比如human behaviors）而言，如何在一个相互连接的模型中，有效的表示时序模式是其分析的重点。当然，有专门的时间序列分析模型，可以用来处理时序性的问题，比如HMM（隐马尔科夫模型），但这些模型并不是这里讨论的重点。

对于一个时序序列的分析而言，一个显而易见的方法就是，将这些时序序列也作为输入向量的一个维度。

举个例子：假设现在分析人的步态行为，如下图所示，这里是经过预处理之后的人的步态行为。很显然，步态行为具有时序性，周期性。
----------

而用传统的神经网络来处理这种具有时序性的步态，所使用的方法，就是用空间来代替时间，将时序性的步态行为并行输入，相当于就是下面这个神经网络图。这里仅仅取了步态周期中的四个状态作为输入的例子，来说明时序并行化的过程，在实际分析过程中，并行输入的步态状态当然会有更多一些。
----------

这个方法有以下三方面的缺点：

1. 这种方法需要一个输入缓冲器（input buffer），在输入缓冲完成之后，才可以一次性的并行输入到神经网络中。且不论在实际的应用场景中，是否有缓冲机制；系统如何知道缓冲的内容可以作为神经网络的输入也是一个需要考究的问题。
2. 这种缓冲机制，相当于一个 定长 的移位寄存器（shift register），也就是说，这需要对输入缓冲做归一化处理，使输入到神经网络的输入向量具有相同的长度。
3. 这份方法很难将时间序列中的相对时序位置和绝对时序位置区分开来，举个简单的例子，下面这幅图中的两个序列显然有相同的模式（111），但是由于在不同的位置上，就很容易被判别为不同模式的序列。
   ----------------------------------

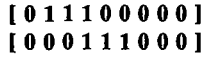
上面讲的这种方法，一般称为时间并行化方法（paralielize time），这种方法相当于增加了一个维度，用来存放时间，并以此成为神经网络的输入。

相对于上面时间并行化的方法而言，一种更好的将时间序列输入到神经网络中的方法，就是这里要说的RNN。这个方法可以让时间序列 按照其本来的样子，输入到神经网络之中。

RNN的产生，就是为了让神经网络对序列性输入拥有处理能力。比如预测一句话的下一个单词是什么，那么就需要基于之前的几个单词来推测，并且前几个单词的顺序很重要。

RNN之所以会被叫做 循环 （recurrent），主要是因为RNN对输入的序列中的每个样本都执行相同的操作，RNN的输出，也是基于以前的计算的。

另一种思考RNN的方法就是，RNN是一种拥有记忆能力的学习器，它对到目前为止所计算过的序列拥有一定的记忆能力。

RNN的核心内容就是使用了循环连接（recurrent links），使用循环链接之后，可以使得神经网络拥有动态记忆能力。所谓循环连接，就像下面这幅图中显示的一样，指的就是隐藏层单元的输出，可以做为输入的一部分，重新进入到神经网络中。

--------------------

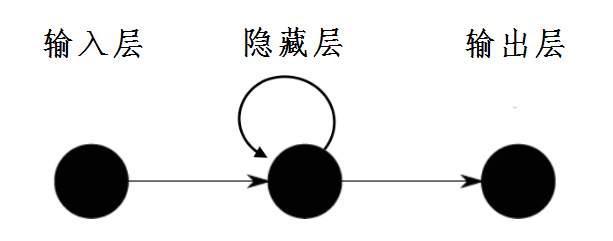
和一般的神经网络不同的是，RNN由于再隐藏层使用了循环链，所以RNN对输入的时间序列并不限制其大小。

从理论上讲，RNN对于输入序列的长度是没有限制的，但是在实际的使用中，我们一般都仅仅往回看几步而已。

RNN包含:
输入单元(Input units)，输入集标记为$\{ x_0, x_1...x_t, x_{t+1} ...\}$;
输出单元(Output units)，输出集标记为$\{y_0,y_1...y_t,y_{t+1}...\}$。
隐藏单元(Hidden units)，其输出集标记为$\{s_0,s_1...s_t,s_{t+1}...\}$

这些隐藏单元完成了最为主要的工作。你会发现，在图中：有一条单向流动的信息流是从输入单元到达隐藏单元的，与此同时另一条单向流动的信息流从隐藏单元到达输出单元。在某些情况下，RNNs会打破后者的限制，引导信息从输出单元返回隐藏单元，这些被称为“Back Projections”，并且隐藏层的输入还包括上一隐藏层的状态，即隐藏层内的节点可以自连也可以互连。

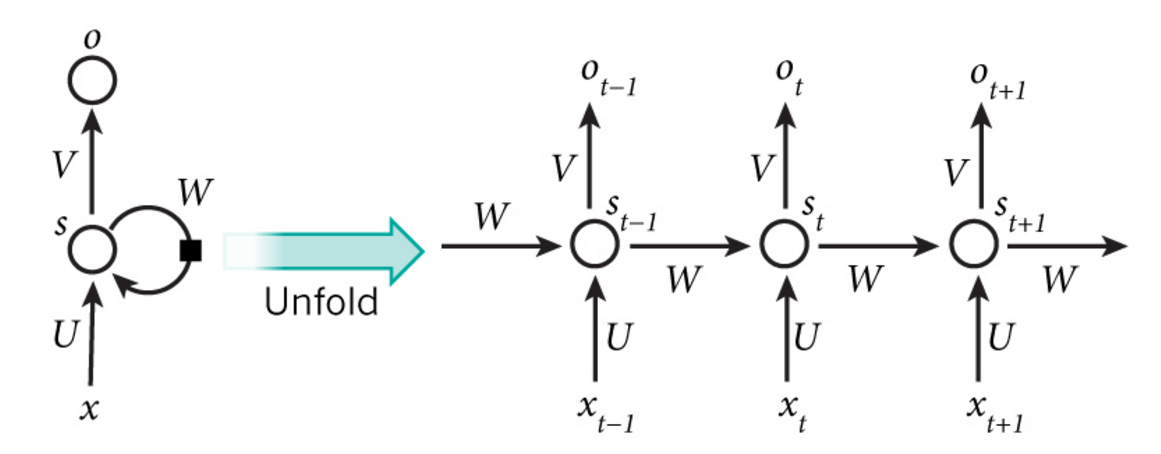
上面这幅图中展示了一个RNN展开成为一个完整的神经网路的过程，一个最简单的展开方式就是，输入序列中有多少个状态，就将隐藏层展开多少次。比如，前面提到的步态识别中，将步态序列归一化成为10个状态，那么一个简单的RNN展开后，就可以在隐藏层展开出10层，并且，每个步态状态对应于展开出来的一个隐藏层。

RNN计算流程：

• $x_t$ 是输入序列在 $t$ 时刻的输入向量。
• $s_t$ 是在 $t$ 时刻隐藏层的输出，这是RNN的记忆单元，$s_t$ 的计算基于前一次隐藏层计算的输出 $s_{t-1}$，以及当前的输入 $x_t$ 。按照上面的图中的计算的话，其计算方法可以如下：$s_t =f( Ws_{t-1}+Ux_{t})$ 。这里的 $f$ 是神经网络中经常选择的一些激活函数，比如 $tanh$ 、$sigmoid$ 、$ReLU$ 等等。当然在计算 $s_1$的时候，需要计算 $s_0$，这里一般直接初始化为0。
• $o_t$ 是步骤 $t$ 时刻的输出，比如如果想预测步态序列中的下一个步态，那么可以得到 $o_t = softmax(Vs_t)$

有几点需要注意：
1. 你可以认为隐藏层状态 $s_t$ 是网络的记忆单元. $s_t$ 包含了前面所有步的隐藏层状态。而输出层的输出$o_t$只与当前步的$s_t$有关。在实践中，为了降低网络的复杂度，往往$s_t$只包含前面若干步而不是所有步的隐藏层状态
2. 在传统神经网络中，每一个网络层的参数是不共享的。而在RNNs中，每输入一步，每一层，各自都共享参数$U,V,W$。这主要是说明RNNs中的每一步都在做相同的事，只是输入不同，因此大大地降低了网络中需要学习的参数
3. 上图中每一步都会有输出，但是每一步的输出并不是必须的。比如，我们需要预测一个步态序列属于哪一个人，我们仅仅需要关心最后一个步态输入后的输出，而不需要知道每个步态输入后的输出。同理，每步的输入也不是必须的。RNNs的关键之处在于隐藏层，隐藏层能够捕捉序列的信息。

对于一个简单的RNN而言，其含有一个输入层 $I$, 隐藏层 $s$， 很多时候这个也被称为状态层或者内容层（state or context layer）,以及输出层 $y$。在 $t$ 时刻RNN的输入层是 $I(t)$，输出是 $y(t)$，$s(t)$ 是隐藏层的输出，而对应的隐藏层的输入为 $x(t)$。

$$x(t)=I(t)+s(t-1)\\ s_j(t)=f(\sum_{i}{x_i(t)u_{ji}})\\ y_k(t)=g(\sum_{j}{s_j(t)v_{kj}})$$

这里的 $f$ 是 $sigmoid$ 激活函数，工作于隐藏层：

$$f(z)=\frac{1}{1+e^{-z}}$$

而这里的 $g$ 是 $softmax$ 函数，工作于输出层：

$$g(z_m) = \frac{e^{z_m}}{\sum_k{e^{z_k}}}$$

如何训练RNN

对RNN的训练，和对传统的神经网络的训练方式基本上是一样的。使用的仍然是反向传播（backpropagation）算法，但和传统的BP算法相比较，又存在一定的区别。将RNN展开就可以发现，RNN的参数被所有的时间点所共享，即：当前的输出不仅仅要依靠当前时间点所计算出来的梯度，同时还依赖于之前时间点上计算得到的梯度。

这一点相对比较容易理解，从上面的公式也可以很容易看出来：在基于$x(t)$计算 $s(t)$的时候，由于$x(t)$是基于$s(t-1)$得到的，所以需要递归的计算$s(t-1)$，这也就是为什么这个算法有时也被叫做递归神经网络的原因。举个简单的例子，在$t=4$时，还需要向后传递三步，已经后面的三步都需要加上各种的梯度。该学习算法称为Backpropagation Through Time (BPTT)。

关于BPTT，后面会进行详细的介绍。现在需要注意的一点是，基于BPTT来训练RNN，由于其训练存在递归的问题，如果RNN的递归深度过长，将使其无法计算。在文章 On the difficulty of training recurrent neural networks 中就有详细的解释和实验，其表明：BPTT无法解决长时依赖问题(即当前的输出与前面很长的一段序列有关，一般超过十步就无能为力了)，因为BPTT会带来所谓的梯度消失或梯度爆炸问题(the vanishing/exploding gradient problem)。当然，有很多方法去解决这个问题，如LSTMs便是专门应对这种问题的。