支持向量机（SVM）

监督学习

---

@author : duanxxnj@163.com
@time : 2016-07-31

---

在看这篇文章之间，建议先看一下感知机，这样可以更好的看懂SVM。

---

---

一、最大间隔分类器

在之前的文章感知机中提到过，感知机模型对应于特征空间中将实例划分为正负两类的分离超平面，但是，感知机的解却不止一个。对同一个数据集而言，可以计算得到很多的感知机模型，不同的感知机的 训练误差 都是一样的，都为0。

那么，这些训练误差都为0的感知机模型中，如何针对当前数据集，选择一个最好的感知机模型呢？现在就需要考虑模型的 泛化误差 了。即，在所有训练误差为0的感知机中，选择泛化误差最小的那个感知机，这就是SVM算法最初的目的。

基本的SVM（最大间隔分类器）是一种二分类模型，它是定义在特征空间上的间隔最大的线性分类器，间隔最大是SVM和感知机不同的地方，间隔最大化对应于泛化误差最小。

---

1.1 决策面

面对一个线性可分的二分类问题，将正负样本分开的超平面，称为决策面。

和 线性回归 模型一样，这里一般会使用一些特征函数$\phi(x)$，将输入空间映射到新的特征空间中，再进行计算。

$$y(x)=f(w^T\phi(x)+b)$$

这里$f(\cdot)$ 叫做激活函数，$w$是线性模型的系数，$b$一般被叫做偏置：

$$f(a)= \begin{cases} +1& \text{a$\ge$0}\\ -1& \text{a<0} \end{cases}$$

这里输出的取值为 $t\in\{+1,-1\}$ ，即正负样本。这里的 $\{+1,-1\}$ 仅仅是一个标号，代表正负样本，并不是具体的数值。如果感觉不喜欢$\{+1,-1\}$，可以和Logistics Regression一样，使用$\{0,1\}$也行。而且，可以使用$\{+1,-1\}$主要也是因为这里是二分类问题，遇到多分类问题的时候，还得考虑其他的标号方式。

如果感觉$\phi(x)$这种表述方式不太习惯，可以考虑所有的$\phi(x)=x$，这样就和一般的书上的公式一致了。这种表达仅仅是我个人的喜好，式主要是为了强调，在实际问题中，输入空间$x$一般不会作为模型的输入，而是要将输入空间通过一定的特征转换算法$\phi(x)$，转换到特征空间，最后在特征空间中做算法学习。而且，在实际问题中，各种算法基本上都是死的，但是，特征变换的这个过程$\phi(x)$却是活的，很多时候，决定一个实际问题能不能很好的解决，$\phi(x)$起着决定性的作用。举个简单的例子，比如Logistics Regression，数据最好要做归一化，如果数据不归一化，那么那些方差特别大的特征就会成为主特征，影响模型的计算，$\phi(x)$就可以做这个事情。再或者后面要降到的核函数问题，核函数SVM能解决非线性可分问题，主要也是基于使用 $\phi(x)$ 来做非线性特征变换。

作为一个决策面：
当样本的标号 $t_n=+1$的时候，该样本为正样本。如果样本被正确分类，那么 $w^T\phi(x_n) + b>0$，$f(w^T\phi(x)+b)=+1$
当样本的标号 $t_n=-1$的时候，该样本为负样本。如果样本被正确分类，那么 $w^T\phi(x_n) + b<0$，$f(w^T\phi(x)+b)=-1$

究竟什么是决策面？
答:决策面就是能够将正负样本分开的点的集合，比如上面的模型中，决策面的数学表达式为：$w^T\phi(x)+b=0$，决策面就是这个式子的解集，所以，一般我们就直接用这个式子代表决策面了。可以看到，对于这个决策面的数学表达式而言，$w$ 和 $b$ 的数值并不重要。比如，$w^T\phi(x)+b=0$ 和 $2w^T\phi(x)+2b=0$，后一个决策面的参数数值是前一个决策面数值的两倍，但这两个决策面的解是一样的，也就是说其得到的点集是一样的，那么这两个表达式所表示的就是同一个决策面。所以，这里我要强调一点，对于一个线性决策面而言，重要的不是$w$ 和 $b$ 的取值，重要的是 $w$ 和 $b$ 的比值， $w$ 和 $b$ 的比值决定了一个决策面的点集，也就决定了一个决策面。

---

1.2 最优决策面

对于线性可分的二分类问题而言，使用 感知机 算法，可以得到很多很多满足上述要求的决策面，比如下图中，就是可以将正负两类数据分开的两个决策面。

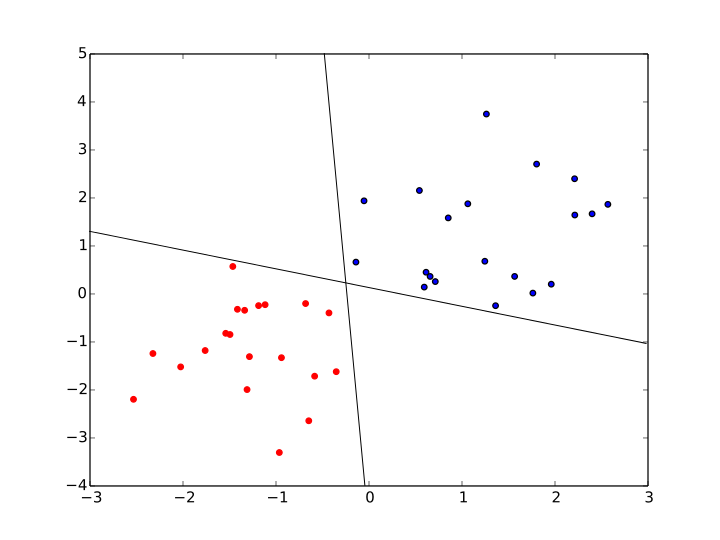
那么，在这些决策面中，哪个决策面，才是最优的决策面呢？首先，需要明确，上述的决策面，都是可以将训练样本正确分类的决策面，也就是说，上述决策面的 训练误差 都为0。要从这些训练误差都为0的模型中，选出一个最好的模型，很自然的，就需要考虑模型的 泛化误差 。

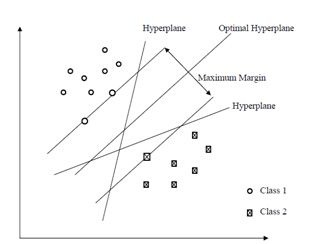
最大间隔分类器认为，决策面的泛化误差可以用训练样本集合中，离决策面最近的样本点到决策面的间隔（margin）来表示，离决策面最近的样本点，到决策面的间隔（margin）越大，那么，这个决策面的泛化误差就越小。直观的来讲，最优决策面差不多就是下面这幅图中，中间的那个决策面。

---

1.3 最小间隔

什么是间隔？
答：首先，要搞清楚是谁和谁的间隔，在这里指的是一个 训练样本点 和 决策面 之间的间隔。

那么，间隔又如何定义的呢？
答：间隔，就是样本点到决策面之间的距离，由中学的知识就可以知道，一个样本点 $x_n$ 到一个面 $w^T\phi(x)+b=0$，的距离为（这里可以直接认为是点到直线的距离）：

$$r_n=\frac{w^T\phi(x_n)+b}{||w||}$$

但这个距离在数值上会存在正负的问题，由于样本点类别取值 $t_n\in\{+1,-1\}$ ，所以样本点到决策面的间隔可以改为：

$$r_n=\frac{t_n\{w^T\phi(x_n)+b\}}{||w||}$$

当 $t_n=+1$的时候，如果样本被正确分类， $w^T\phi(x_n) + b>0$，上述样本点到决策面的间隔 $r_n$ 取正值
当 $t_n=-1$的时候，如果样本被正确分类， $w^T\phi(x_n) + b<0$，上述样本点到决策面的间隔 $r_n$ 仍然取正值
这样，分类正确的样本点的间隔就永远是正的了。

显然，一旦决策面有了，那么训练集合中的每个样本点 $x_n$ 到决策面都会有一间隔 $r_n$ 。自此，就可以定义样本集合到决策面最小的间隔 $r$ 为：

$$r=\min_{n}\frac{t_n\{w^T\phi(x_n)+b\}}{||w||};n\in\{1,2,...,N\}$$

既然 $r$ 是最小间隔，毫无疑问，对于任意一个样本点 $x_n$ 而言：

$$\frac{t_n\{w^T\phi(x_n)+b\}}{||w||} \ge r$$

---

1.4 最小间隔最大化

前面已经说了，要使用决策面在训练样本中的最小间隔 $r$ 来表示决策面的训练误差：最小间隔 $r$ 越大，那么其泛化误差就越小，模型就越好。而我们这里，就是在所有可选的决策中，找出其对应的最小间隔 $r$ 最大的那个决策面，而决策面是用参数 $w$ 和 $b$ 定义的，所以，最小间隔最大化可以形式化为：

$$arg \max_{w,b}\{\min_{n}\frac{t_n\{w^T\phi(x_n)+b\}}{||w||}\}$$

用优化理论的形式重写一下上面的式子，可以得到：

$$\max_{w,b} r\\ st：\frac{t_i\{w^T\phi(x_i)+b\}}{||w||} \ge r ~~~; i=1,2,...N$$

将上面的约束条件变一下型可得：

$$\max_{w,b} r\\ st： t_i\{w^T\phi(x_i)+b\} \ge r{||w||} ~~~; i=1,2,...N$$

在前面已经提到过，对于一个决策面$w^T\phi(x_i)+b=0$ 而言， 重要的不是$w$ 和 $b$ 的取值，$w^T\phi(x)+b=0$ 和 $2w^T\phi(x)+2b=0$ 的所得到的$x$的点集是一样的，即其决策面是一样的，这里真正重要的是 $w$ 和 $b$ 的比值。

$w$ 和 $b$ 的比值，决定了一个决策面的点集，也就决定了一个决策面。

所以，只要有一个决策面，那么，唯一确定的是$w$ 和 $b$ 的比值，但是，$w$ 和 $b$ 具体的取值是可以改变的，只要$w$ 和 $b$ 按比例改变，决策面就是确定不变的。

也就是说，$w$ 和 $b$ 的比值比值不变的情况下，$w$是可以任意取值的。这样的话，为了便于计算，我们就取：

$$||w||=\frac{1}{r}$$

那么，上面的式子又可以改写为：

$$\max_{w,b} \frac{1}{||w||}\\ st： t_i\{w^T\phi(x_i)+b\} \ge 1 ; i=1,2,...N$$

可以看到，上面的式子最大化的目标函数变成了 $1/||w||$ ，很容易知道，其等价于 最小化 $||w||^2$ ，那么最小间隔最大化，最终就可以变为下面这个最小化的约束优化问题：

$$\min_{w,b} ||w||^2\\ st： t_i\{w^T\phi(x_i)+b\} \ge 1 ; i=1,2,...N$$

这里，最小间隔为：

$$r=\frac{1}{||w||}$$

在网上博客还有现有的书籍中，对于最小间隔最大化的解释，都使用了函数间隔和几何间隔的概念，我个人在第一次接触这两个概念的时候，就有些被弄糊涂了，理解了这两个概念之后，又感觉这种解释过于冗余、牵强，完全是为了解释最小间隔最大化而解释最小间隔最大化。所以，这里我直接抛弃函数间隔和几何间隔的概念，给出我个人的一种解释。

最小间隔最大化后得到的决策面，就是我们要找的泛化误差最小的决策面。对于下图中两特征的二分类问题而言，可以看出， 最小间隔为$1/||w||$，即，正样本到决策面的最小间隔为$1/||w||$；同时，负样本到决策面的最小间隔也为$1/||w||$。所以正负样本之间的最小间隔为$2/||w||$。

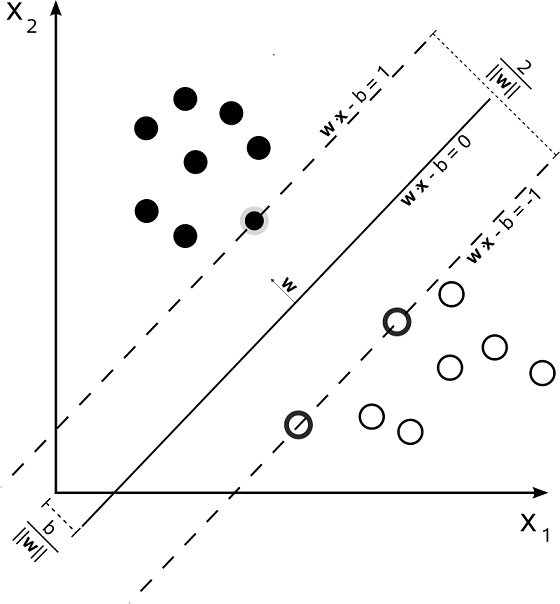
由于间隔最小的样本点 $x_n$ 满足：

$$\frac{t_n\{w^T\phi(x_n)+b\}}{||w||}=r=\frac{1}{||w||}$$

所以，间隔最小的正样本点 $x_n$ 满足：

$${w^T\phi(x_n)+b}=1$$

间隔最小的负样本点 $x_n$ 满足：

$${w^T\phi(x_n)+b}=-1$$

这里定义，拥有最小间隔的正负样本点为支持向量（support vector），也就是上图中${w^T\phi(x_n)+b}=1$ 和 ${w^T\phi(x_n)+b}=-1$ 所对应的那三个样本点。

关于支持向量机的名字，这里可以稍微说一下，因为这个名字并不是特别的好理解。首先是支持（support），根据柯林斯词典，support的主要意思：the activity of providing for or maintaining by supplying with money or necessities，表示的是提供一些必须品的意思。vector指的就是样本点，这个问题不大。那么问题来了，为什么将间隔最小的那些样本点叫做support vector（或者可以直接说是support point）呢？答：从图中可以看出，对于决策面而言，要想唯一的确定这个决策面，就是要根据最小的间隔 $r$ 来得到，也就是说，决策面仅仅和拥有最小间隔的那些样本点相关，和其他那些间隔大于最小间隔的样本点，是没有关系的。即：拥有最小间隔的那些样本点是决策面所必须的，而间隔大于最小间隔的样本点的有无，对决策面并不构成影响。所以将拥有最小间隔的那些样本点叫做support point， 也就是support vector。

---

1.5 拉格朗日对偶性

在求解约束最优化问题的过程中，我们常常会使用拉格朗日对偶性（Lagrange duality），把原始问题（primal problem）转换为对偶问题（dual problem）来求解，基于对偶问题的求解来得到原始问题的解。这个方法在统计学中经常使用，不仅仅本文的SVM算法用到了拉格朗日对偶性，后面要讲的最大熵模型也用到了拉格朗日对偶性。这里仅仅对拉格朗日对偶性做一个简述，我个人认为，主要知道其概念和结果即可，无需深究。拉格朗日对偶性的详细说明，可以参见Boyd的《Convex Optimization》，该书用一整个章节的篇幅来详细的论述了拉格朗日对偶性的问题。

对于一个线性规划问题，我们称之为原始问题，都有一个与之对应的线性规划问题我们称之为对偶问题。原始问题与对偶问题的解是对应的，得出一个问题的解，另一个问题的解也就得到了。并且原始问题与对偶问题在形式上存在很简单的对应关系：
- 目标函数对原始问题是极大化，对偶问题则是极小化
- 原始问题目标函数中的系数，是对偶问题约束不等式中的右端常数，而原始问题约束不等式中的右端常数，则是对偶问题中目标函数的系数
- 原始问题和对偶问题的约束不等式的符号方向相反
- 原始问题约束不等式系数矩阵转置后，即为对偶问题的约束不等式的系数矩阵
- 原始问题的约束方程数对应于对偶问题的变量数，而原始问题的变量数对应于对偶问题的约束方程数
- 对偶问题的对偶问题是原始问题

1、原始问题

假设，有$f(x),c_i(x),h_j(x)$，他们是定义在空间$R^n$上的连续可微的函数，也就是可导函数的意思。其约束最优化问题为：

$$\begin{aligned} \min_{x\in R^n} f(x)\\ s.t. ~~c_i(x) &\le 0; i=1,2,...,k\\ h_j(x) &= 0; j=1,2,...,l \end{aligned}$$

这里$c_i(x)$是不等式优化，而$h_j(x)$是等式优化。

上面这种约束优化问题的形式成为原始问题。

现在，引入拉格朗日函数：

$$L(x,\alpha,\beta)=f(x)+\underbrace{\sum_{i=1}^k{\alpha_i c_i(x)}}_{不等式约束}+\underbrace{\sum_{j=1}^l{\beta_j h_j(x)}}_{等式约束}$$

这里 $\alpha_i$ 和 $\beta_j$ 是拉格朗日乘子，且，$\alpha_i \ge 0$。也就是说，不等式约束 $c_i(x)$ 的拉格朗日乘子要大于等于0，而等式约束 $h_j(x)$ 的拉格朗日乘子并没有限制。

现在考虑最大化这个拉格朗日函数，定义：

$$\theta_p(x)=\max_{\alpha,\beta;\alpha_i \ge 0}L(x,\alpha,\beta)=\max_{\alpha,\beta;\alpha_i \ge 0}\{f(x)+\sum_{i=1}^k{\alpha_i c_i(x)}+\sum_{j=1}^l{\beta_j h_j(x)}\}$$

对于上面的最大化式子有：

• 如果不等式约束 $c_i(x) < 0$ ，等式约束 $h_j(x)=0$ ，那么上式最大化就会使得 $\alpha_i = 0$，$\beta_j$ 可以取任意值。 此时所有满足约束条件的，并且最大化结果为$\theta_p(x)= f(x)$。
• 如果不等式约束 $c_i(x) = 0$ ，等式约束 $h_j(x)=0$，那么上式最大化就会使得 $\alpha_i >0$ ,$\beta_j$ 可以取任意值。此时是满足约束条件的，并且最大化结果为$\theta_p(x)= f(x)$。
• 如果存在不等式约束 $c_i(x) > 0$ , 等式约束 $h_j(x)=0$，即此时存在不等式约束违反约束条件，那么要使得上式最大化，必然会使得 $\alpha_i = \infty$ ，进而使得 $\theta_p(x)= \infty$。
• 如果不等式约束 $c_i(x) \le 0$ , 存在 $h_j(x) \neq 0$ ，那么要使得上式最大化，必然会使得 $\beta_j = \infty$ ，进而使得 $\theta_p(x)= \infty$。

综上所述，可以知道：

$$\theta_p(x)=\max_{\alpha,\beta;\alpha_i \ge 0}L(x,\alpha,\beta)= \begin{cases} f(x)& \text{$c_i(x) \le 0$ 和 $h_j(x)=0$ 都满足时}\\ \infty& \text{当存在违反$c_i(x) \le 0$ 或者$h_j(x)=0$ 条件时} \end{cases}$$

由于原始最优化问题就是要在满足约束条件下，求解最小化的$f(x)$。而由上可知，在满足约束条件的情况下，$f(x)=\theta_p(x)=\max_{\alpha,\beta;\alpha_i \ge 0}L(x,\alpha,\beta)$。

也就是说，原始约束最优化问题：

$$\begin{aligned} \min_{x\in R^n} f(x)\\ s.t. ~~c_i(x) &\le 0; i=1,2,...,k\\ h_j(x) &= 0; j=1,2,...,l \end{aligned}$$

中的 $f(x)，c_i(x) \le 0，h_j(x) = 0$ 就可以用 $\theta_p(x)=\max_{\alpha,\beta;\alpha_i \ge 0}L(x,\alpha,\beta)$ 来代替。

于是乎，原始约束最优化问题就变成了一个极小极大化的问题：

$$\min_x \theta_p(x)=\min_x \max_{\alpha,\beta;\alpha_i \ge 0}L(x,\alpha,\beta)$$

很显然，这个极小极大化问题，和原始问题是等价的。

为了方便，这里定义原始问题（primal problem）的最优解为：

$$p^* = \min_x \theta_p(x)$$

2、对偶问题

对于一块磁铁而言，磁铁有N极和S极，N极和S极只是同一块磁铁的不同表现而已，这两个极性虽然不同，但是却拥有相同的本质：磁。他们是相辅相成的，是同一个事物的两种不同表现。就像有阴必有阳；有光明必有黑暗；而阴阳本为一体，明暗实为一物，他们都是同一个东西的不同表现而已，这个是世间万物的规律。

对偶问题和原始问题也是一样，他们是优化问题的两个不同表现形式而已，他们本质上是一个东西，只是表现的方式相反罢了。

考虑原始问题：

$$\theta_p(x)=\max_{\alpha,\beta;\alpha_i \ge 0}L(x,\alpha,\beta)$$

原始问题是以 $\alpha,\beta$ 为参数，以 $x$ 为变量的极大化问题。既然对偶问题是原始问题关于优化问题的相反的表达方式，那么对偶问题就可以写成，以 $\alpha,\beta$ 为变量，以 $x$ 为参数的极小化问题(记住一点：本质相同，表现相反):

$$\theta_D(\alpha,\beta)=\min_{x}L(x,\alpha,\beta)$$

原始问题最终是被极小化，成为了一个极小极大化的问题：

$$\min_x \theta_p(x)=\min_x \max_{\alpha,\beta;\alpha_i \ge 0}L(x,\alpha,\beta)$$

对偶问题，要和其相反，就需要被极大化，而称为一个极大极小化的问题：

$$\max_{\alpha,\beta;\alpha_i \ge 0} \theta_D(\alpha,\beta)= \max_{\alpha,\beta;\alpha_i \ge 0} \min_x L(x,\alpha,\beta)$$

上面的式子，就称为拉个朗日函数的极大极小问题，并定义对偶问题（dual problem）的最优解为：

$$d^*=\max_{\alpha,\beta;\alpha_i \ge 0} \theta_D(\alpha,\beta)$$

由于：

$$\theta_D(\alpha,\beta)=\min_{x}L(x,\alpha,\beta) \le L(x,\alpha,\beta) \le \max_{\alpha,\beta;\alpha_i \ge 0}L(x,\alpha,\beta) \le \theta_p(x)$$

所以：

$$\theta_D(\alpha,\beta) \le \theta_p(x)$$

上面这是式子说明，$\theta_D(\alpha,\beta)$的所有的解，都不大于$\theta_p(x）$的解。那么，毫无疑问，对偶问题的最优解和原始问题的最优解也满足这个式子：

$$d^*=\max_{\alpha,\beta;\alpha_i \ge 0} \theta_D(\alpha,\beta) \le \min_x \theta_p(x) = p^*$$

在我们常见的问题中，只要满足一定的条件，就可以使得$d^*=p^*=L(x^*,\alpha^*,\beta^*)$，这里 $x^*,\alpha^*,\beta^*$ 就是最优解。这里所说的一定的条件，指的就是KKT条件。

3、KKT条件

对于原始问题 和 对偶问题而言，$x^*,\alpha^*,\beta^*$ 分别是原始问题和对偶问题的解的充分必要条件是 $x^*,\alpha^*,\beta^*$ 满足KKT条件：

$$\begin{aligned} \nabla_x L(x^*,\alpha^*,\beta^*) &= 0\\ \nabla_\alpha L(x^*,\alpha^*,\beta^*) &= 0\\ \nabla_\beta L(x^*,\alpha^*,\beta^*) &= 0\\ \alpha_i^*c_i(x^*) &=0; i=1,2...k\\ c_i(x^*) &\le 0 ; i=1,2...k\\ \alpha_i^* &\ge 0; i=1,2...k\\ h_j(x^*) &= 0; j=1,2,...l \end{aligned}$$

上述的KKT条件，看起来很吓人，其实很容易理解：函数 $L(x,\alpha,\beta)$ 是以 $x,\alpha,\beta$ 为参数的，那么其最优解 $x^*,\alpha^*,\beta^*$ 定然满足 函数 $L(x,\alpha,\beta)$ 的梯度为0，这就是KKT条件的前三个等式：

$$\begin{aligned} \nabla_x L(x^*,\alpha^*,\beta^*) &= 0\\ \nabla_\alpha L(x^*,\alpha^*,\beta^*) &= 0\\ \nabla_\beta L(x^*,\alpha^*,\beta^*) &= 0 \end{aligned}$$

前面已经说明过，函数 $L(x,\alpha,\beta)$ 要能够使用，最初的优化问题必须满足不等式约束$c_i(x) \le 0$ 以及其相关的拉格朗日乘子 $\alpha_i$ 的约束：

$$\begin{aligned} \alpha_i^*c_i(x^*) &=0; i=1,2...k\\ c_i(x^*) &\le 0 ; i=1,2...k\\ \alpha_i^* &\ge 0; i=1,2...k\\ \end{aligned}$$

而最后一个KKT条件，对应的就是 $L(x,\alpha,\beta)$ 的等式约束:

$$h_j(x^*) = 0; j=1,2,...l$$

---

1.6 最小间隔最大化求解

求解最小间隔最大化，就是要求解式子：

$$\min_{w,b} \frac{1}{2}||w||^2\\ s.t. ~~ t_i\{w^T\phi(x_i)+b\} \ge 1 ; i=1,2,...N$$

而求解上面的式子，用的到方法，就是拉格朗日对偶性。这里，在原来的最小化的目标函数前面加了 $1/2$ ,并不会影响最后的最优解，但是对后面的公式推导相对有利，故而加上了个 $1/2$。

将它作为原始的优化问题，应用拉格朗日对偶性，通过求解对偶问题（dual problem）来得到原始问题（primal problem）的最优解，这个最优解，就对应于最优的决策面。

这样做的优点主要有两个：
一、对偶问题相对来说比较容易求解
二、可以很自然的引入核函数，进而推广到非线性分类器中

首先，构建拉格朗日函数，由于上面的约束优化问题中只有不等式约束，所以为所有的不等式约束添加拉格朗日乘子： $\alpha_i \ge 0;i=1,2,...N$，则拉格朗日函数为：

$$L(w,b,\alpha)=\underbrace{\frac{1}{2}||w||^2}_{优化目标}\underbrace{-\sum_{i=1}^N{\alpha_i(t_i\{w^T\phi(x_i)+b\} - 1)}}_{不等式约束}$$

根据前面关于拉格朗日对偶性的说明可以很容易知道，这个原始问题为极小极大问题：

$$\min_{w,b}\max_{\alpha;\alpha_i \ge 0} L(w,b,\alpha)$$

其对应的对偶问题为极大极小问题：

$$\max_{\alpha;\alpha_i \ge 0} \min_{w,b} L(w,b,\alpha)$$

求解内部极小化

这里首先求解内部的极小化问题：

$$\min_{w,b} L(w,b,\alpha)$$

显然，这个极小化问题是以 $w,b$ 为参数的，那么，先使$L(w,b,\alpha)$ 对 $w,b$ 求导，并令其为0：

$$\begin{aligned} \nabla_w L(x,\alpha,\beta) &= w-\sum_{i=1}^N{\alpha_it_i\phi(x_i)}=0\\ \nabla_b L(x,\alpha,\beta) &= \sum_{i=1}^N{\alpha_i t_i}=0 \end{aligned}$$

那么，就有：

$$w=\sum_{i=1}^N{\alpha_it_i\phi(x_i)}\\ \sum_{i=1}^N{\alpha_i t_i}=0$$

将 $w=\sum_{i=1}^N{\alpha_it_i\phi(x_i)}$ 带入到 $L(w,b,\alpha)$ 中，就可以得到：

$$\begin{aligned} L&=\frac{1}{2}||w||^2-\sum_{i=1}^N{\alpha_i(t_i\{w^T\phi(x_i)+b\} - 1)}\\ &=\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\{\alpha_i \alpha_j t_i t_j <\phi(x_i),\phi(x_j)>\} - \sum_{i=1}^N{\alpha_i(t_i\{\{\sum_{j=1}^{N}{\alpha_j t_j \phi(x_j)}\}\phi(x_i)+b\} - 1)}\\ &=-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\{\alpha_i \alpha_j t_i t_j <\phi(x_i),\phi(x_j)>\} + b\sum_{i=1}^N{\alpha_i t_i} + \sum_{i=i}^{N}{\alpha_i}\\ &=-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\{\alpha_i \alpha_j t_i t_j <\phi(x_i),\phi(x_j)>\} + \sum_{i=i}^{N}{\alpha_i} \end{aligned}$$

上面推导的导数第二步使用了：$\sum_{i=1}^N{\alpha_i t_i}=0$，最终可以得到：

$$\min_{w,b} L(w,b,\alpha) = -\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\{\alpha_i \alpha_j t_i t_j <\phi(x_i),\phi(x_j)>\} + \sum_{i=i}^{N}{\alpha_i}$$

这里的$<\phi(x_i),\phi(x_j)>$ 是 $\phi(x_i)$ 和 $\phi(x_j)$ 的內积。

求解外部极大化

前面已经将内部的极小化求解得到了$\min_{w,b} L(w,b,\alpha)$，这里再在其求解的结果上加上外层的极大化，那么就有下面这个约束优化问题：

$$\max_\alpha \{ -\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\{\alpha_i \alpha_j t_i t_j <\phi(x_i),\phi(x_j)>\} + \sum_{i=i}^{N}{\alpha_i}\}$$

$$\begin{aligned} s.t. ~~ \sum_{i=1}^N{\alpha_i t_i}&=0\\ \alpha_i &\ge 0;i=1,2,...N \end{aligned}$$

这个就是原问题的对偶问题，当然了，可以将这个对偶问题的目标函数的符号换一下，让它成为一个最小化的问题:

$$\min_\alpha \{ \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\{\alpha_i \alpha_j t_i t_j <\phi(x_i),\phi(x_j)>\} - \sum_{i=i}^{N}{\alpha_i}\}$$

$$\begin{aligned} s.t. ~~ \sum_{i=1}^N{\alpha_i t_i}&=0\\ \alpha_i &\ge 0;i=1,2,...N \end{aligned}$$

公式推导到这个地方，就可以知道，上面这个最小化问题，就是我们最终要求解的问题，其最小化的目标函数是以 $\alpha$ 为参数的。

也就是说，假设最优解是 $\alpha^*=（\alpha_1^*,\alpha_2^*,...\alpha_N^*）$。这里暂时不讨论如何求得这个最优解，其具体的求解算法会在后面详细的论述，现在假设，我们可以通过某种算法，将上面的这个最小化的优化问题的最优解求出来。

那么，在已知这个最优解的情况下，我们来看一下，基于这个最优解，SVM的决策面是什么样的？

根据原始问题$L(w,b,\alpha)$的KKT条件可以知道：

$$\begin{aligned} \nabla_w L(x^*,\alpha^*,\beta^*) &= w^*-\sum_{i=1}^N{\alpha_i^* t_i \phi(x_i)}=0\\ \nabla_b L(x^*,\alpha^*,\beta^*) &= \sum_{i=1}^N{\alpha_i^* t_i}=0\\ \alpha_i^*(t_i\{w^{*T}\phi(x_i)+b^*\} - 1) &= 0;i=1,2,...N\\ t_i\{w^{*T}\phi(x_i)+b^*\} - 1 &\ge 0;i=1,2,...N\\ \alpha_i^* &\ge 0;i=1,2,...N \end{aligned}$$

那么，就有：

$$w^*=\sum_{i=1}^N{\alpha_i^* t_i \phi(x_i)}$$

这里，根据已经求得的 $\alpha_i^*$ ,就可以将 $w^*$ 求出来了。决策面的参数有两个: $w,b$，$w$ 求出来了，剩下的就是 $b$ 了。

在前面讨论过，SVM是间隔最大化的决策面，支持向量对应的就是间隔最小的那些点，由前面关于间隔最大化的讨论可以知道，支持向量满足下面这个公式：

$$t_i\{w^T\phi(x_i)+b\} - 1=0$$

而根据前面对原始问题的讨论，可以知道，满足这个公式的点 $x_i$ （支持向量） ,在拉格朗日函数中，所对应的 $\alpha_i^*> 0$ 。所以，我们只需要找到一个$\alpha_i^*> 0$ , 就可以得到 $b^*$:

$$b^*=\frac{1}{t_i}-w^{*T}\phi(x_i)$$

同时，需要注意：$t_i^2=1$，并带入 $w^{*T}$，就可以将上面这个式子重写为：

$$b^*=t_i - \sum_{j=1}^N{\alpha_j^* t_j <\phi(x_j),\phi(x_i)>}$$

当然，为了稳妥起见，很多时候，我们会将所有的支持向量 $x_i\in S$ 对应的 $b_i^*$ 都求出来，然后用其均值，作为最终的 $b^*$。这里 $S$ 是支持向量的集合，也就是 $\alpha_i^* > 0$ 所对应的点集:

$$b^*=\frac{1}{N_s}\sum_{i=1}^{N_s}{b_i^*}$$

这样，就可以求得最终的决策超平面为：

$$\sum_{i=1}^N\{\alpha_i^* t_i <\phi(x_i),\phi(x)>\} + b^*=0$$

分类决策函数可以写为：

$$f(x)=sign\{\sum_{i=1}^N\{\alpha_i^* t_i <\phi(x_i),\phi(x)>\} + b^*\}$$

这里就可以发现:

• 在预测的时候，$w^*$ 和 $b^*$ 仅仅依赖于训练集合中 $\alpha_i^* > 0$ 的那些样本点，而其他样本点对$w^*$ 和 $b^*$ 没有影响。但是，为了求得 $w^*$ 和 $b^*$ ，在训练阶段，还是需要整个样本集合。也就是说，在做预测的时候，支持向量机需要的内存空间是非常小的，只需要存储支持向量即可，预测过程和非支持向量无关。
• 分类决策函数仅仅依赖于输入$x$ 和 训练样本之间的內积。这个內积是后面核函数的雏形，也是SVM得以广泛应用的关键。

---

1.7 SVM、LDA、Logistics Regression 算法比较

在之前的文章线性判别分析（Linear Discriminant Analysis）中就说过：凡是分类算法，必定有决策面，而这些分类算法所不同的是:决策面是线性的还是非线性的；以及如果得到这个决策面。

对于Logistics Regression

对于一个二分类问题，在Logistics Regression中，假设后验概率为Logistics 分布：

$$P(C_1|x)=\frac{1}{1+exp(w^Tx)}\\ P(C_2|x)==\frac{exp(w^Tx)}{1+exp(w^Tx)}$$

这里，使用一个单调的变换函数，logit 函数：$log[p/(1-p)]$，那么就可以得到：

$$log \frac{P(C_1|x)}{P(C_2|x)}=w^Tx$$

所以Logistics Regression的决策面就是：

$$w^Tx=0$$

对于Linear Discriminant Analysis

这里假设$f_k(x)$是类别$C_k$的类条件概率密度函数，$\pi_k$ 是类别$C_k$的先验概率，毫无疑问有$\sum_{k} \pi_k = 1$。根据贝叶斯理论有：

$$P(C_k|x)=\frac{f_k(x) \pi_k}{\sum_{l=1}^K f_l(x) \pi_l}$$

LDA假设$f_k(x)$是均值不同，方差相同的高斯分布，所以其类条件概率密度函数可以写为：

$$f_k(x)=\frac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}}exp(-\frac{1}{2}(x-\mu_k)^T \Sigma^{-1}(x-\mu_k))$$

这里，特征$x$的维度为$p$维，类别$C_k$的均值为$\mu_k$，所有类别的方差为$\Sigma$。

LDA和前面提到的Logistics Regression采用的单调变换函数一样，都是logit 函数：$log[p/(1-p)]$，对于二分类问题有：

$$\begin{aligned} log\frac{P(C_1|x)}{P(C_2|x)} &= log \frac{f_1(x)}{f_2(x)} + log\frac{\pi_1}{\pi_2}\\ &= x^T \Sigma^{-1}(\mu_1-\mu_2) - \frac{1}{2}(\mu_1+\mu_2)^T\Sigma^{-1}(\mu_1-\mu_2) + log\frac{\pi_1}{\pi_2} \end{aligned}$$

所以LDA的决策面就是：

$$x^T \Sigma^{-1}(\mu_1-\mu_2) - \frac{1}{2}(\mu_1+\mu_2)^T\Sigma^{-1}(\mu_1-\mu_2) + log\frac{\pi_1}{\pi_2}=0$$

显然，在LDA中，和Logistics Regression不同的是，LDA的决策面是由各个数据分布的方差和类别中心决定的。

对于SVM

对于SVM而言，我么假设，最大间隔会带来最小的泛化误差。但是，反过来思考，这个假设真的是真确的吗？在讨论LDA和Logistics Regression的时候，我们其实也是说他们的决策面是最优的。那么，到底那个算法得到的决策面才是最好的呢？

说到这个问题，让我突然想起来前段时间的一件事情，一同学面试，面试官问他：Logistics Regression对数据分布有什么要求？他并不知道怎么回答，后来回来和他们实验室的人讨论了许久，也没有结果。其实这个回答非常的简单：

我们所面对的所有的机器学算法，都是有适用范围的，或者说，我们所有的机器学习算法都是有约束的优化问题。而这些约束，就是我们在推导算法之前所做的假设。

比如：Logistics Regression，上面已经明确说明了，在Logistics Regression中，假设后验概率为Logistics 分布；再比如：LDA假设$f_k(x)$是均值不同，方差相同的高斯分布；这些都是我们在推导算法之前所做的假设，也就是算法对数据分布的要求。

而对于SVM而言，它并没有对原始数据的分布做任何的假设，这就是SVM和LDA、Logistics Regression区别最大的地方。这表明SVM模型对数据分布的要求低，那么其适用性自然就会更广一些。如果我们事先对数据的分布没有任何的先验信息，即，不知道是什么分布，那么SVM无疑是比较好的选择。

但是，如果我们已经知道数据满足或者近似满足高斯分布，那么选择LDA得到的结果就会更准确。如果我们已经知道数据满足或者近似满足Logistics 分布，那么选择Logistics Regression就会有更好的效果。

通过这三个方法的比较，我只想说明一件事情：机器学习算法是死的，但，人是活的。使用什么机器学习算法，是根据实际问题要求，和数据的具体分布而定的。

---

---

二、软间隔最大化分类器

在这篇文章之前所有的讨论中，假设，所面对的数据在特征空间$\phi(x)$中是线性可分的，那么，最终得到的SVM可以在输入空间$X$中得到一个准确的判别面，尽管其对应的判别面可能是一个非线性判别面。

然而，在现实的数据中，数据是线性不可分的（或者近似线性可分）。换一种说法就是：类条件分布存在重叠。如果这样，上面讲的算法最终只会有两种结果：1、决策面会出现严重的震荡，而无法收敛；2、即便收敛到了一个非线性的决策面，其决策面也会十分的复杂，泛化能力低。

因此，我们就需要对原始的SVM算法做一定的改动，让它对数据的要求，从线性可分扩展到线性不可分。即：允许部分训练数据存在分类错误的情况，以得到一个相对比较好的决策面。 这个改动后的SVM一般被称为 软间隔最大化分类器 ，而与之相对应的，前面论述的只可以解决线性可分数据的SVM，称为 硬间隔最大化分类器 。

---

2.1 软间隔最大化分类器的两个问题

那么，现在就有两个问题摆在我们面前：

1.在SVM中，对于非线性可分的数据而言，哪些样本点是存在分类错误的样本点？
2.对于分类错误的点，软间隔最大化分类器 如何处理以得到相对比较好的决策面？

两个问题，就是软间隔最大化分类器的核心问题，回答了这两个问题，掌握了软间隔最大化分类器。

哪些是分类错误的样本点

首先必须要知道，面对一个非线性可分的数据集，哪些样本点是分类错误的样本点？可以先看下面这幅图：

图中，左边那幅图对应的是数据线性可分时，SVM的状态。此时有决策面：$x^T \beta + \beta_0=0$ ，也就是之前讨论的 $x^T w + b =0$ ，只是写法不同而已。根据前面“最小间隔最大化”小章节的讨论可知：最小间隔为$M=1/||\beta||$，也就是之前的表达式：$r=1/||w||$。这种状态，是所有数据点都分类正确，且最小间隔最大分类的状态。

图中，右边那幅图对应的就是数据线性不可分时，SVM的状态。此时决策面依然是：$x^T \beta + \beta_0=0$，最小间隔仍然为$M=1/||\beta||$。不过，右图中$\xi_i^*;i=1,2...5$ 就是非线性可分数据在SVM中分类错误的点。

那么总结一下，在非线性可分的情况下，样本点的状态一共有下面五种：
1.非支持向量，即是在 $margin$ 两侧，被正确分类的样本点。这些样本点对于SVM的决策面没有贡献。
2.在$margin$边界上面的点，这个是支持向量，且被正确分类。
3.在$margin$内部，被正确分类的点，比如$\xi_1^*,\xi_2^*,\xi_4^*$，这些也是支持向量。
4.在决策面上的点，这些点可以拒绝判断，也可以直接认为是分类正确的点。
5.真正的被分类错误的点：$\xi_3^*,\xi_5^*$，这些点直接走到了决策面的另一边去了。

很容易发现，相对于数据线性可分的情况而言，非线性可分数据的状态多了三种情况，也就是上面五种情况的后三种，线性可分的数据只存在前面两种情况。

而后面三种情况的样本点的间隔，都比最小间隔 $r$ 也就是图中的 $M$ 要小一些，所以，后面这三种情况，就是SVM认为的错误的样本点（即便情况3、情况4样本被分类正确了），软间隔最大化分类器 就是要针对后面这三种情况来做文章。

---

分类错误的样本点的处理:软间隔变量

前面提到了，后面三种情况的样本点的间隔，都比最小间隔 $r$ 也就是图中的 $M$ 要小一些。这里首先要考虑的问题就是，如何用公式来表达后面这三种情况？这里就引入了一个最小间隔 $r$ 的比例因子：软间隔变量 $\xi$。$\xi$是最小间隔 $r$ 的比例系数，或者叫做倍数。下面先分别讨论如何将软间隔变量 $\xi$ 应用到上面的后三种情况中：

• 对于前面第三种情况：在$margin$内部，被正确分类的点，比如$\xi_1^*,\xi_2^*,\xi_4^*$。这些点的间隔为：

  $$\xi_i^*=\xi_i*r; ~~~~0 < \xi_i < 1$$

• 对于前面第四种情况：在决策面上的点，这些点的间隔为：

  $$\xi_i^*=\xi_i*r; ~~~~\xi_i = 1$$

• 对于前面第五种情况：真正的被分类错误的点：$\xi_3^*,\xi_5^*$，这些直接走到了决策面的另一边去了的点，这些点的间隔为：

  $$\xi_i^*=\xi_i*r; ~~~~\xi_i > 1$$

为了将前面的第一种情况：非支持向量，即是在 $margin$ 两侧，被正确分类的样本点。和第二种情况：在$margin$边界上面的点，这个是支持向量，且被正确分类。也统一的用软间隔变量 $\xi$来表示，这里将SVM的优化公式重写为下面这个形式：

$$\max_{w,b} r\\ st：\frac{t_i\{w^T\phi(x_i)+b\}}{||w||} \ge r(1-\xi_i) ; ~~i=1,2,...N\\ \xi_i \ge 0 ; i=1,2,...N$$

而前面第一种情况和第二种情况所对应的 $\xi_i=0$。

和“最小间隔最大化”章节中讨论的一样，$w$ 和 $b$ 的 比值 不变的情况下，$w$是可以任意取值的。这样的话，为了便于计算，我们就取：

$$||w||=\frac{1}{r}$$

那么，上面的式子又可以改写为：

$$\max_{w,b} \frac{1}{||w||}\\ st： t_i\{w^T\phi(x_i)+b\} \ge 1 - \xi_i; i=1,2,...N\\ \xi_i \ge 0 ; i=1,2,...N$$

可以看到，上面的式子是最大化 $1/||w||$ ，很容易知道，其等价于 最小化 $||w||^2$ ，那么最小间隔最大化，最终就可以变为下面这个式子：

$$\min_{w,b} ||w||^2\\ st： t_i\{w^T\phi(x_i)+b\} \ge 1 - \xi_i; i=1,2,...N\\ \xi_i \ge 0 ; i=1,2,...N$$

这里，最小间隔为：

$$r=\frac{1}{||w||}$$

---

2.2 软间隔最大化分类器 的优化公式

上面提到的第五种情况，真正的被分类错误的点：$\xi_3^*,\xi_5^*$，这些直接走到了决策面的另一边去了的点，所对应的 $\xi_i > 1$。如果说我们知道 $\sum_{i=1}^N \xi_i \le K$ ,那么，就可以说，这个 软间隔最大化分类器 的训练错误样本数，最多为 $K$个。让训练误差尽量的小也是我们的一个优化目标，这样，软间隔最大化分类器 就成了一个多目标的优化问题：

$$\min_{w,b} \frac{1}{2}||w||^2\\ \min_{\xi}\sum_{i=1}^N \xi_i\\ st： t_i\{w^T\phi(x_i)+b\} \ge 1 - \xi_i; i=1,2,...N\\ \xi_i \ge 0 ; i=1,2,...N$$

由于上面两个优化目标的限制条件是一样的，可以将两个优化目标合成一个优化目标：

$$\min_{w,b,\xi} \{\frac{1}{2}||w||^2 + C\sum_{i=1}^N \xi_i\}\\ st： t_i\{w^T\phi(x_i)+b\} \ge 1 - \xi_i; i=1,2,...N\\ \xi_i \ge 0 ; i=1,2,...N$$

这里的参数 $C$ 是损失参数（cost parameter），用于权衡$||w||^2$ 和 $\sum_{i=1}^N \xi_i$。一般我们将$||w||^2$视为模型的复杂度，而将$\sum_{i=1}^N \xi_i$视为模型的错误率，损失参数 $C$ 就是在模型复杂度和模型的错误率之间找一个平衡，这个值一般作为模型的一个输入变量，需要人工设置：

• C 越小，模型越偏向于最小化$||w||^2$，而忽略$\sum_{i=1}^N \xi_i$，这样模型非常简单，但模型的错误率相对较高。
• C 越大，模型越偏向于最小化$\sum_{i=1}^N \xi_i$，而忽略$||w||^2$ ，这样模型的错误率相对较低，但模型相对较为复杂。

需要强调：$\xi_i$是对于SVM而言，分类错误的样本点 $x_i$ 的分类错误间隔相对于最小间隔 $r$ 的比例。我们不可能让错误的比例无限的增长，那样分类错误就太大了。所以，我们需要对错误间隔进行限制，而限制的手段，就是为总的错误间隔比例加一上限：$\sum \xi_i \le constant$。这是软间隔最大化分类器 优化公式的另一种解释。

---

2.3 软间隔最大化分类器 的对偶问题

这里的步骤和 1.5 拉格朗日对偶性 几乎雷同，首先将 软间隔最大化分类器 的优化公式转换为拉个朗日函数的形式，其原始的优化公式为：

$$\min_{w,b,\xi} \{\frac{1}{2}||w||^2 + C\sum_{i=1}^N \xi_i\}\\ st： t_i\{w^T\phi(x_i)+b\} \ge 1 - \xi_i; i=1,2,...N\\ \xi_i \ge 0 ; i=1,2,...N$$

拉个朗日函数为：

$$L(w,b,\xi,\alpha , \mu)=\underbrace{\frac{1}{2}||w||^2 + C\sum_{i=1}^N \xi_i}_{优化目标} \underbrace{-\sum_{i=1}^N \alpha_i\{{t_i\{w^T\phi(x_i)+b\} - 1 + \xi_i}\}-\sum_{i=1}^N{\mu_i\xi_n}}_{不等式约束}$$

其中，$\alpha_i , \mu_i$ 为拉格朗日乘子。将 $L(w,b,\xi,\alpha , \mu)$ 分别对 $w, b, \xi$ 求偏导:

$$\begin{aligned} \nabla_w L(w,b,\xi,\alpha , \mu) &= w-\sum_{i=1}^N{\alpha_it_i\phi(x_i)}=0\\ \nabla_b L(w,b,\xi,\alpha , \mu) &= \sum_{i=1}^N{\alpha_i t_i}=0\\ \nabla_{\xi_i} L(w,b,\xi,\alpha , \mu) &= C-\alpha_i-\beta_i=0;i=1,2,..N \end{aligned}$$

就可以得到：

$$w=\sum_{i=1}^N{\alpha_it_i\phi(x_i)}\\ \sum_{i=1}^N{\alpha_i t_i}=0\\ C-\alpha_i-\beta_i=0;i=1,2..N$$

将上面三个式子带入到 $L(w,b,\xi,\alpha , \mu)$ 中，和之前 1.6 最小间隔最大化求解 中的推导一样，最终可以得到：

$$\min_{w,b,\xi} L(w,b,\xi,\alpha , \mu) = -\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\{\alpha_i \alpha_j t_i t_j <\phi(x_i),\phi(x_j)>\} + \sum_{i=i}^{N}{\alpha_i}$$

这里的$<\phi(x_i),\phi(x_j)>$ 是 $\phi(x_i)$ 和 $\phi(x_j)$ 的內积。

再对$\min_{w,b,\xi} L(w,b,\xi,\alpha , \mu)$求极大化，即可得到 软间隔最大化分类器 的对偶问题：

$$\max_\alpha \{ -\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\{\alpha_i \alpha_j t_i t_j <\phi(x_i),\phi(x_j)>\} + \sum_{i=i}^{N}{\alpha_i}\}$$

$$\begin{aligned} s.t. ~~ \sum_{i=1}^N{\alpha_i t_i}&=0\\ C-\alpha_i-\mu_i&=0\\ \alpha_i &\ge 0\\ \mu_i&\ge0;i=1,2,...N \end{aligned}$$

这个就是原问题的对偶问题，当然了，可以将这个对偶问题的目标函数的符号换一下,,让它成为一个最小化的问题，并将后面三个式子做一个合并:

$$\min_\alpha \{ \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\{\alpha_i \alpha_j t_i t_j <\phi(x_i),\phi(x_j)>\} - \sum_{i=i}^{N}{\alpha_i}\}$$

$$\begin{aligned} s.t. ~~ \sum_{i=1}^N{\alpha_i t_i}&=0\\ 0 \le \alpha_i &\le C;i=1,2,...N \end{aligned}$$

这就是 软间隔最大化分类器 的对偶问题，和前面相比，这里的对偶问题只是限制条件 $0 \le \alpha_i \le C$ 和前面不同，其他的是一模一样的。

---

2.4 软间隔最大化分类器 求解

很显然，得到了软间隔最大化分类器 的对偶形式之后，其优化求解出来的就是最优解 $\alpha^*$。这里再次说明：假设 $\alpha^*$我们已经通过某种算法得到了，至于这个算法是什么后面的章节会详细的说明，这里不同担心。

仿照 1.5 拉格朗日对偶性 中的公式推导 ，假设 $x^*,\alpha^*,\xi^*,\alpha^* , \mu^*$ 为最优解，可以很容易推出 软间隔最大化分类器 拉格朗日优化的KKT条件为：

$$\begin{aligned} \nabla_w L(x^*,\alpha^*,\xi^*,\alpha^* , \mu^*) &= w^*-\sum_{i=1}^N{\alpha_i^* t_i \phi(x_i)}=0\\ \nabla_b L(x^*,\alpha^*,\xi^*,\alpha^* , \mu^*) &= \sum_{i=1}^N{\alpha_i^* t_i}=0\\ \nabla_{\xi} L(x^*,\alpha^*,\xi^*,\alpha^* , \mu^*) &= C-\alpha_i-\mu_i=0\\ \alpha_i^*(t_i\{w^{*T}\phi(x_i)+b^*\} - 1+\xi_i^*) &= 0;i=1,2,...N\\ t_i\{w^{*T}\phi(x_i)+b^*\} - 1 + \xi_i^* &\ge 0;i=1,2,...N\\ \alpha_i^* &\ge 0;i=1,2,...N\\ \mu_i^*\xi_i^* &= 0;i=1,2,...N\\ \xi_i^* &\ge 0;i=1,2,...N\\ \mu_i^* &\ge 0;i=1,2,...N \end{aligned}$$

在假设知道 $\alpha^*$ 的情况下，由KKT条件的第一个公式：$\nabla_w L(x^*,\alpha^*,\xi^*,\alpha^* , \mu^*) = w^*-\sum_{i=1}^N{\alpha_i^* t_i \phi(x_i)}=0$ 可以知道，$w$的最优解为：

$$w^*=\sum_{i=1}^N{\alpha_i^* t_i \phi(x_i)}$$

再找到一个 $0 < \alpha_j < C$ ，其所对应的样本点满足：$t_i\{w^{*T}\phi(x_i)+b^*\} - 1 = 0$，那么，就可以和前面的推导一样，得到：

$$b^*=\frac{1}{t_i}-w^{*T}\phi(x_i)$$

同时，需要注意：$t_i^2=1$，并带入 $w^{*T}$，就可以将上面这个式子重写为：

$$b^*=t_i - \sum_{j=1}^N{\alpha_j^* t_j <\phi(x_j),\phi(x_i)>}$$

当然，为了稳妥起见，很多时候，我们会将所有的支持向量 $x_i\in S$ 对应的 $b_i^*$ 都求出来，然后用其均值，作为最终的 $b^*$。这里 $S$ 是支持向量的集合，也就是 $\alpha_i^* > 0$ 所对应的点集:

$$b^*=\frac{1}{N_s}\sum_{i=1}^{N_s}{b_i^*}$$

这样，就可以求得最终的决策超平面为：

$$\sum_{i=1}^N\{\alpha_i^* t_i <\phi(x_i),\phi(x)>\} + b^*=0$$

分类决策函数可以写为：

$$f(x)=sign\{\sum_{i=1}^N\{\alpha_i^* t_i <\phi(x_i),\phi(x)>\} + b^*\}$$

---

2.5 对参数 $\alpha,\xi$ 的讨论

基于上面的推导，可以很容易的看出，软间隔最大化分类器 就是在 硬间隔最大化分类器 的基础上，处理非线性可分的数据。而参数$\alpha,\xi$起着决定样本点类别的作用，那么，这里就对这两个参数做一下讨论，看看这两个参数是如何判断非线性可分数据集中的样本点的类别的。

为了方便，这里直接用一张表格说明参数$\alpha,\xi$ 和样本点之间的关系，图种叉叉的部分，说明这种情况并不存在，下面将对这个表格做详细的说明：

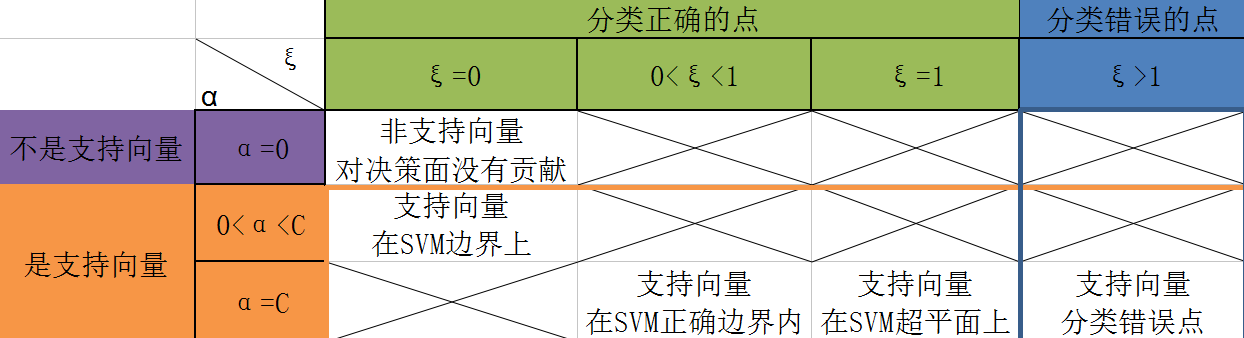
在 2.1 软间隔最大化分类器的两个问题 中，就讨论过，非线性可分情况下，SVM中的样本点一共有五种情况，也就是上面表格中的所对应的五种情况。

从表格中可以粗略的观察到：
- 当$\alpha_i =0$ 时，对应的样本点是非支持向量；当$\alpha_i >0$ 时，对应的样本点是支持向量
- 当$\xi \le1$ 时，对应的样本点可以被正确的分类；当$\xi >1$ 时，对应的样本点分类错误

现在基于参数 $\alpha、\xi$ 对上面五种情况再做更详细的讨论：

1.当$\xi_i=0,\alpha_i=0$时，此时的样本点 $x_i$ 并不是支持向量，其被完全的分类正确，样本点满足：$t_i\{w^T\phi(x_i)+b\} > 1$。
变量关系：当$\alpha_i=0$时，由KKT条件中的第三条：$C-\alpha_i-\mu_i=0$可以知道，$\mu_i=C$；再由KKT条件第七条：$\mu_i^*\xi_i^* = 0$ 可以知道：$\xi_i=0$；最后根据KKT条件的第四条和第五条，可以很容易知道：$t_i\{w^T\phi(x_i)+b\} > 1$。

2.当$\xi_i=0,0<\alpha_i<C$时,此时样本点刚好在SVM的间隔边界上，是支持向量，被正确分类，样本点满足：$t_i\{w^T\phi(x_i)+b\} = 1$。
变量关系：当$0<\alpha_i<C$ 时，由KKT条件中的第三条：$C-\alpha_i-\mu_i=0$可以知道，$0<\mu_i<C$;再由KKT条件第七条：$\mu_i^*\xi_i^* = 0$，可以知道：$\xi_i=0$。最后根据KKT条件的第四条和第五条，可以很容易知道：$t_i\{w^T\phi(x_i)+b\} = 1$。

3.当$0<\xi_i<1,\alpha_i=C$时，此时样本点在SVM的正确的间隔边界内，是支持向量，被正确分类，样本点满足：$0< t_i\{w^T\phi(x_i)+b\} < 1$。
变量关系：当$\alpha_i=C$时，由KKT条件中的第三条：$C-\alpha_i-\mu_i=0$可以知道，$\mu_i=0$;再由KKT条件第六、七条：$\xi_i^* \ge 0 ；\mu_i^*\xi_i^* = 0$，可以知道：$\xi_i>0$。根据KKT条件的第四条和第五条，可以很容易知道：$t_i\{w^T\phi(x_i)+b\} = 1-\xi_i$。那么，此时$0<\xi_i<1$,所以$0<t_i\{w^T\phi(x_i)+b\} < 1$，即，其对应的样本点在分类正确的间隔中。

4.当$\xi_i=1,\alpha_i=C$时，此时样本点在SVM决策面上，是支持向量，被正确分类，样本点满足：$t_i\{w^T\phi(x_i)+b\} = 0$。
变量关系：这里的变量关系的分析和第三种情况一样，差别仅仅是 $\xi_i=1$，由：$t_i\{w^T\phi(x_i)+b\} = 1-\xi_i$，可以很容易知道：$t_i\{w^T\phi(x_i)+b\} = 0$ ，这样，样本点$x_i$就刚好在SVM的决策面上了。

5.当$\xi_i>1,\alpha_i=C$时，是支持向量，被错误分类，样本点满足：$t_i\{w^T\phi(x_i)+b\} < 0$。
变量关系：这里的变量关系的分析和第三种情况一样，差别仅仅是 $\xi_i>1$，由：$t_i\{w^T\phi(x_i)+b\} = 1-\xi_i$，可以很容易知道：$t_i\{w^T\phi(x_i)+b\} < 0$ ，这样，样本点$x_i$就在决策面错误的一边，被错误分类了。

由于变量$\alpha$是我们最终要求解的变量，这里再单独对变量$\alpha$做一个总结。首先，这里取$g(x)$如下，即SVM的决策面函数:

$$g(x)=\sum_{i=1}^N\{\alpha_i t_i <\phi(x_i),\phi(x)>\} + b$$

那么，根据前面的表格，可以很容易得到：

$$\begin{aligned} \alpha_i=0 &\Leftrightarrow t_ig(x_i) \ge 1\\ 0<\alpha_i<C &\Leftrightarrow t_ig(x_i) = 1\\ \alpha_i=C &\Leftrightarrow t_ig(x_i) \le 1 \end{aligned}$$

总的来说就是：

• 在SVM间隔区间外的点，对应的$\alpha_i=0$
• 在SVM间隔区间边缘上的点，对应的$0<\alpha_i<C$
• 在SVM间隔区间内部的点，对应的$\alpha_i=C$

---

---

三、基于核函数的非线性SVM

使用上面提到的 软间隔最大化分类器 在一定程度上，可以解决非线性可分问题。但是，其实质上是用一个线性的决策面，在允许部分训练样本点出现分类错误的前提下，得到的SVM。软间隔最大化分类器 对于数据是近似线性可分的情况，效果还是不错的，但是对于完全的线性不可分的情况，其分类效果就不太好了。此时，就需要通过某种手段，将SVM从线性分类器扩展成为非线性分类器，而这个手段，就是“核技巧”。

核技巧在机器学习中的应用是非常的广泛的，特别是从2000年之后，各个大牛们对核技巧的研究也越来越深入，这里仅仅对核技巧做一些简单的说明，方便在SVM中使用，后面会使用专门的文章来详细讨论核技巧。

在前面对SVM的推导中，最后得到的判别函数为：

$$f(x)=sign\{\sum_{i=1}^N\{\alpha_i^* t_i <\phi(x_i),\phi(x)>\} + b^*\}$$

上式中有两个东西需要格外注意，$\phi(x_i)$和<\phi(x_i),\phi(x)>

$\phi(x_i)$所代表的就是一种空间映射，是核技巧必备的一个元素，这也是为什么本文从一开始推导SVM的公式的时候，使用的就是$\phi(x)$而不是单纯的$x$的原因。

$<\phi(x_i),\phi(x)>$ 指的是 $\phi(x_i),\phi(x)$ 的內积。这里可以看到，SVM的判别函数最终变成了$\phi(x_i),\phi(x)$的內积的求解。

实际上，这两点，就是核技巧的核心，下面分别对这两点进行说明：

---

3.1 特征映射解决非线性可分问题

一般来说，如果能用一个超曲面将正负训练样本完全分开，则称这种问题为非线性可分问题。

非线性可分问题一般是非常的难求的，对于近似线性可分的非线性可分问题，还可以考虑使用上面的 软间隔最大化的SVM来得到一个分类器，但是如果数据非线性十分的强，以至于无法近似线性分开的时候，我们一般就考虑对数据空间做一个空间变换，将维度提升，在低维空间中非线性可分的问题，在高维空间中可能变成线性可分的问题，在高维空间中训练一个线性分类器，对数据进行分类。

注意：维度提升后，在高维空间，是可能变成线性可分！！！是可能！！！，说白了，数据从低维空间映射到高维空间之后，到底会成什么状态，没人说得准。虽然从低维到高维之后，数据是否线性可分，存在不确定性，但也不失为一种有效的手段，并且，其在实际的应用中表现的也还不错。这个就像深度学习算法一样，那货到底干了什么事情，没人说得准，反正最终效果还不错。

提升维度的过程大致可以从下面这个例子中看出来：

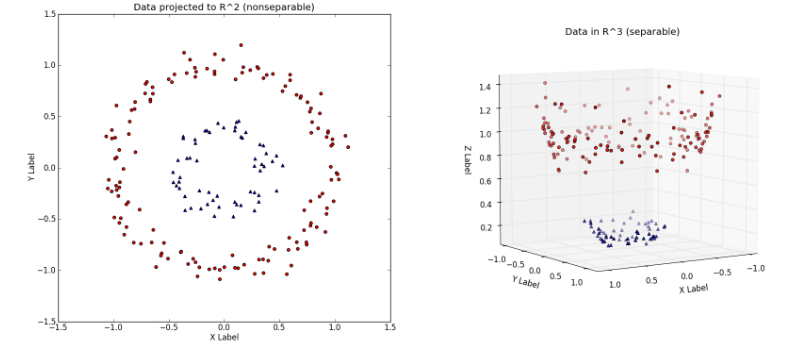
左图中对应的就是原始数据，显然左图中的数据是线性不可分的。然后通过映射：

$$[x_1,x_2]=>[x_1,x_2,x_1^2+x_2^2]$$

将数据从原始特征空间映射到新的特征空间。即，原始特征空间$X$是二维的,$X$中的样本点可以用$[x_1,x_2]$来表示，新的特征空间$Z$是三维的，$Z$中的样本点可以用$[z_1,z_2,z_3]$来表示。这样，上面的映射过程，就可以表示为：

$$z_1=x_1\\ z_2=x_2\\ z_3=x_1^2+x_2^2$$

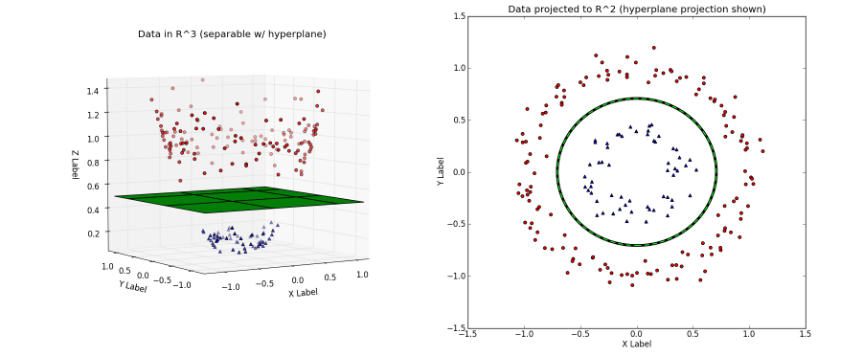
左图对应的是新的空间中，用一个平面就将变换后的数据分开；右图则对应原始空间中需要一个分线性的决策面，才可以将数据分开。

可以很容易的看出，在新的特征空间$Z$中，数据已经是线性可分的了。这就是提升数据维度，使得原空间的分线性可分问题变成新空间的线性可分问题的过程。

上面的例子说明，用线性模型求解非线性分类问题分为两个步骤：1、首先使用一个变换，将原空间的数据$X$映射到更高维度的新空间$Z$；2、在新的数据空间$Z$中,用线性分类学习方法，从训练数据中学习模型。

---

3.2 核函数$K(x_1,x_2)$

前面也提到过，在前面对SVM的推导中，最后得到的判别函数为：

$$f(x)=sign\{\sum_{i=1}^N\{\alpha_i^* t_i <\phi(x_i),\phi(x)>\} + b^*\}$$

从公式中可以明显看出，对这个判别函数的求解最终变成了对$<\phi(x_i),\phi(x)>$的计算。这里的$\phi(x)$就是上面提到的特征变换，用于解决非线性可分的问题。

按照一般的思维方式，要求解$<\phi(x_i),\phi(x)>$，那么，就需要我们先定义$\phi(x)$，再根据$x_i,x$，分别计算出 $\phi(x_i),\phi(x)$，最后计算出它们的內积。

这是一个非常繁琐的步骤，而且，由于对高维空间具体的数据分布知之甚少，我们并不能确定一个映射$\phi(x)$是否一定能够使得原始数据在高维空间中线性可分，所以一般也很难确具体的映射公式定$\phi(x)$；或者说，我们一般很难显式的定义出$\phi(x)$。

既然如此，是否可以将$<\phi(x_i),\phi(x)>$直接看成一个函数，不显式的定义$\phi(x)$，而是给定了$x_i,x$后，就直接将$<\phi(x_i),\phi(x)>$计算出来的方法呢？有！这就是核函数！！！！

核函数的定义：假设，将原始的输入空间为$X$（可能是欧式空间 $R^n$ 或者是一个离散集合），新的特征空间为$Z$(希尔伯特空间)，如果存在一个从$X$到$Z$的映射：

$$\phi(x): X\to Z$$

使得对所有的$x_1,x_2 \in X$,函数$K(x_1,x_2)$满足条件：

$$K(x_1,x_2)=<\phi(x_1),\phi(x_2)>$$

则称$K(x_1,x_2)$为一个核函数。其中$\phi(x)$为映射函数，$<\phi(x_1),\phi(x_2)>$为$\phi(x_1),\phi(x_2)$的內积。

基于前面的讨论，可以得出结论:核技巧的想法就是，在学习与预测中，仅仅定义核函数$K(x_1,x_2)$，而不显式的定义映射函数$\phi(x)$。

一般来说，直接计算$K(x_1,x_2)$相对比较容易，而通过<\phi(x_1),\phi(x_2)>的计算反而比较的复杂。

映射函数$\phi(x)$一般是将原始空间的维度升高，有时候会变成无穷维度。

---

3.3 非线性映射定$\phi(x)$与核函数$K(x_1,x_2)$的关系

• 对于给定的函数$K(x_1,x_2)$，其映射后的空间$Z$，可以使多样的，即可以映射到不同的特征空间中
• 对于给定的函数$K(x_1,x_2)$，即便映射到相同维度的特征空间，其映射函数$\phi(x)$也存在多样性

为了说明上面这两个特点，这里举个例子：假设，输入空间是$X=R^2$,核函数是$K(x_1,x_2)=(x_1*x_2)^2$
1. 取特征空间$Z=R^3$，即维度升高一个维度，此时$\phi(x)$可以取：

$$\phi(x)=[(x^{(1)})^2,\sqrt{2} x^{(1)}x^{(2)},(x^{(2)})^2]^T$$

或者也可以取：

$$\phi(x)=\frac{1}{\sqrt{2}}[(x^{(1)})^2-(x^{(2)})^2,2 x^{(1)}x^{(1)},(x^{(1)})^2+(x^{(2)})^2]^T$$

1. 取特征空间$Z=R^4$，即维度升高两个维度，此时$\phi(x)$可以取：

$$\phi(x)=[(x^{(1)})^2,x^{(1)}x^{(2)},x^{(1)}x^{(2)},(x^{(2)})^2]^T$$

---

3.4 常用的核函数

此处本应该讲讲，如何来构造核函数的，但是这个知识点实在是太过复杂，直接放在后面专门讲核技巧的文章中。

一个函数是否能称为核函数，是有非常严格的要求的，但是，我们在实际的使用中，一般都会使用一些常用的核函数，这里提供四个最常用的核函数，关于这些常用核函数的说明，也将放在后面专门讲核函数的文章中。

1.Polynomial 核函数：

$$K(x,z)=(x,z)^d;d \in N$$

2.Gaussian 核函数：

$$K(x,z)=exp(-\frac{||x-z||^2}{2\sigma^2});\sigma > 0$$

3.Sigmoid 核函数：

$$K(x,z)=tanh(\alpha <x,z>+\beta);\alpha>0,\beta>0$$

4.RBF 核函数：

$$k(x,z)=exp(-\rho d(x,z));\rho > 0,d(x,z)是任意的距离度量$$

---

3.5 对无穷维度的定性理解

每次在读一些关于核函数的书籍或者网上的博客的时候，总是会提到：核函数不需要显示的定义特征空间$Z$以及特征映射$\phi(x)$，使得学习算法隐式的在高维的特征空间中进行，甚至可以在无穷维度中进行。

这句话的前部分，已经说明过了，核函数的确不需要显示的定义特征空间$Z$以及特征映射$\phi(x)$，就是可以完成学习过程。但是，甚至可以在无穷维度中进行到底是怎么回事？我所看到的书籍和网络博客中，却没有进一步的讨论。我在这里做一个简略的说明，这需要会涉及一些核函数构造的知识，比较复杂，这里仅仅做定性的分析，详细的讨论也会放在后面专门讲解核技巧的文章中。

在高等数学中，有无穷级数的概念，举个简单的例子：

$$exp(x)=\sum_{n=0}^{\infty}{\frac{x^n}{n!}};-\infty<x<\infty$$

根据上面这个无穷级数的式子，可以很容易的推断出，指数型的核函数，可以变成无穷维度的多项式映射的结果：

$$k(x,z)=exp(k_1(x,z))\\ =\sum_{m=0}^{\infty}\frac{(k_1(x,z))^m}{m!}$$

对于Gaussian 核函数:

$$K(x,z)=exp(-\frac{||x-z||^2}{2\sigma^2});\sigma > 0$$

由于这是一个指数型的核函数，根据前面的讨论，可以定性的判断出，基于无穷级数，Gaussian 核函数的映射函数，可以是无穷维度的。其具体的公式会在后面专门讲核函数的文章中说明，这里仅仅是一个定性的理解。

下面，以一分代码来说明一下SVM的应用：

# -*- coding: utf-8 -*-
"""
@author: duanxxnj@163.com
@time: 2015-07-17_13-59
SVM分类算法示例
为了绘图方便，这里仅仅使用iris数据集的前两个特征作为样本特征
LinearSVC 使用的是平方合页损失
SVC（kernel=‘linear’） 使用的是正则化合页损失
LinearSVC 使用留一法（one-vs-rest）处理多类问题
SVC 使用的是one-vs-one的方法处理多类问题
从图中很容易看出one-vs-rest方法和one-vs-one所产生的决策面的区别
"""
print __doc__
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
# 导入iris数据
# 这个数中一共有三个类别
# 每个类别50个样本
# 每个样本有四个特征
iris = datasets.load_iris()
X = iris.data[:, [2, 3]] # 这里仅仅两个特征作为样本特征
y = iris.target
C = 1.0 # SVM正则化参数
# 使用线性核学习SVM分类器
svc = svm.SVC(kernel='linear', C=C).fit(X, y)
# 直接使用线性SVM分类器
linear_SVC = svm.LinearSVC(C=C).fit(X, y)
# 使用rbf（径向基）核学习SVM分类器
rbf_svc = svm.SVC(kernel='rbf', gamma=0.7, C=C).fit(X, y)
# 使用多项式核学习SVM分类器
poly_svc = svm.SVC(kernel='poly', degree=3, C=C).fit(X, y)
# 生成绘图用的网格
x0_min, x0_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x1_min, x1_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx0, xx1 = np.meshgrid(np.arange(x0_min, x0_max, 0.02),
                       np.arange(x1_min, x1_max, 0.02))
titles = ['SVC with linear kernel',
          'LinearSVC',
          'SVC with RBF kernel',
          'SVC with polynomial kernel']
color = ['r']*50 + ['g']*50 + ['b']*50
for i, clf in enumerate((svc, linear_SVC, rbf_svc, poly_svc)):
    plt.subplot(2, 2, i + 1)
    plt.subplots_adjust(wspace=0.4, hspace=0.4)
    z = clf.predict(np.c_[xx0.ravel(), xx1.ravel()])
    z = z.reshape(xx0.shape)
    plt.contourf(xx0, xx1, z, cmap=plt.cm.Paired, alpha=0.8)
    plt.scatter(X[:, 0], X[:, 1], c=color)
    plt.xlabel('feature_1')
    plt.ylabel('feature_2')
    plt.xlim(xx0.min(), xx0.max())
    plt.ylim(xx1.min(), xx1.max())
    plt.title(titles[i])
plt.show()

---

---

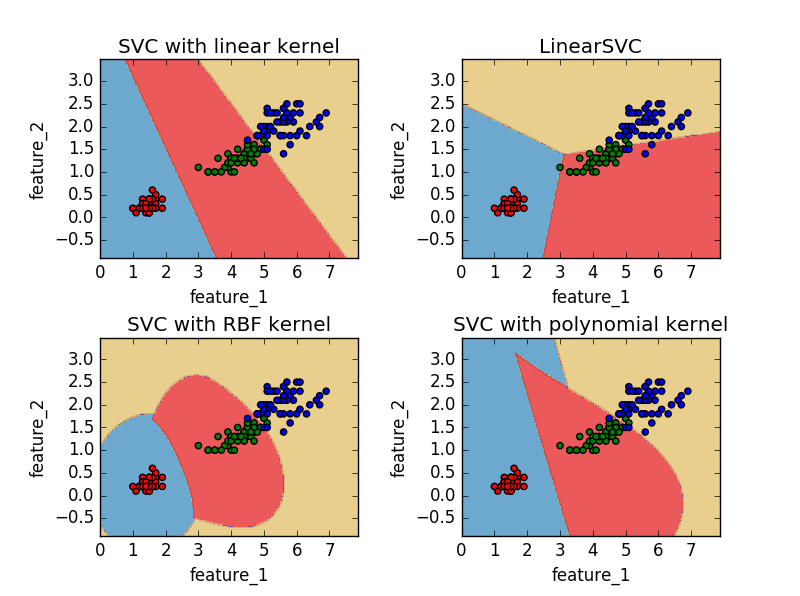
其实，关于SVM算法，如果是入门，看到这个地方，就已经不用再往下深究了。后面是SMO算法的推导，如果不清楚，并不影响SVM的理解。

---

---

四、SMO算法

前面已经得到 软间隔最大化分类器 的对偶问题，现在基于核函数，可将对偶问题写为如下形式：

$$\min_\alpha \{ \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\{\alpha_i \alpha_j t_i t_j K(x_i,x_j)\} - \sum_{i=i}^{N}{\alpha_i}\}$$

$$\begin{aligned} s.t. ~~ \sum_{i=1}^N{\alpha_i t_i}&=0\\ 0 \le \alpha_i &\le C;i=1,2,...N \end{aligned}$$

其KKT条件为：

$$\begin{aligned} \alpha_i=0 &\Leftrightarrow t_ig(x_i) \ge 1\\ 0<\alpha_i<C &\Leftrightarrow t_ig(x_i) = 1\\ \alpha_i=C &\Leftrightarrow t_ig(x_i) \le 1 \end{aligned}$$

其中：

$$g(x)=\sum_{i=1}^N\{\alpha_i t_i K(x_i,x_j)\} + b$$

直接在求解SVM的时候，都是说，假设已经将 $\alpha^*$ 求了出来，然后再计算 $w^*,b^*$的，但是并没有说明，如果计算 $\alpha^*$，这里就来说明一下 $\alpha^*$的计算。

在上面这个问题中，变量就是拉格朗日乘子 $\alpha$ ，且每个变 $\alpha_i$ 都和一个样本点 $x_i$ 相对应，也就是说，变量的个数，是训练样本的数目 $N$。 一般来说，$N$ 是一个非常大的数目，使用普通的凸优化算法，虽然肯定可以将上面的问题解出来，但是算法耗时太长，就需要一种相对简单的算法来得到 $\alpha^*$。这样的算法有很多， 这里就其中最流行的算法 SMO（Sequential Minimal Optimization）做一个介绍。

本文关于 SMO算法的说明，主要参考的是 Platt, John C.《 Fast training of support vector machines using sequential minimal optimization》,1998。

由于有 $N$ 个变量，所以基于训练样本训练SVM是一个非常大的 quadratic programming （QP）optimization problem，即二次最优化问题，在这里也就是上面的软间隔最大化分类器 的对偶问题，这个优化问题在实际中太大，以至于几乎无法得到优化结果。

SMO算法将原始的非常大的 QP优化问题 分解成了一系列非常小的可解的QP优化问题。SMO算法最诱人的地方在于，这些分解后的小的 QP优化问题 ，都是拥有解析解的，也就是说，求解这些小的 QP优化问题 不需要通过非常耗时的循环来得到问题的结果。这样SMO算法的空间复杂度是训练样本的线性函数，这就是使得 SMO 算法可以处理特别大的样本集合的训练问题。由于不需要矩阵计算，使得 SMO算法 在实际的数据集的测试中，其计算复杂度介于线性复杂度和二次复杂度之间。SMO算法的计算复杂度和SVM的模型也有关系，线性核SVM计算速度较快。在实际测试中发现，如果训练样本是稀疏数据集（sparse data sets）,那么，SMO算法的效率会极其高。

---

4.1 最小的QP优化问题

对于SVM的 QP优化问题 ，由于有下面这个限制条件：

$$\sum_{i=1}^N{\alpha_i t_i}=0$$

所以最小的 QP优化问题 仅仅包含两个拉格朗日乘子 $\alpha_i,\alpha_j$ 的优化。

这个原因很简单，这里朗格朗日乘子的数目一共有个 $N$ 个，如果一次只优化其中的一个拉格朗日乘子$\alpha_i$的话，就需要将剩下的所有的$N-1$个拉格朗日乘子固定住。但是由于有上面这个等式限制，剩下的所有的$N-1$个拉格朗日乘子一旦被固定住之后，拉格朗日乘子$\alpha_i$也会被固定住，就无法优化了。这里假设被优化的是 $\alpha_1$，如果只固定这一个变量，那么就有：

$$\alpha_1=\sum_{i=2}^N{\alpha_i t_i}=const$$

所以，这里最小的优化子问题是优化两个拉格朗日乘子$\alpha_i,\alpha_j$，而固定住其他所有的变量。

SMO算法的每一步都是做两件事情：1、选择两个拉格朗日乘子；2、优化这两个拉格朗日乘子。按照原文的说法就是：an analytic method for solving for the two Lagrange
multipliers, and a heuristic for choosing which multipliers to optimize。一个解两拉格朗日乘子的解析算法、一个启发式的拉格朗日乘子选择方法。

---

4.2 二变量拉格朗日乘子解法

由于原始的 QP优化问题，是$N$个变量的，为了求解二变量的 QP优化问题 ，首先需要对约束条件进行分析，然后在此约束条件下求极小值。

不失一般性，这里假设所选择的两个拉格朗日乘子是 $\alpha_1,\alpha_2$ ，而其余的变量 $\alpha_i(i=3,4..N)$都是固定不变的。

原始的约束条件如下：

$$\begin{aligned} s.t. ~~ \sum_{i=1}^N{\alpha_i t_i}&=0\\ 0 \le \alpha_i &\le C;i=1,2,...N \end{aligned}$$

由于现在仅仅考虑两个拉格朗日乘子是 $\alpha_1,\alpha_2$，所以约束条件可以改写为下面这个形式:

$$\begin{aligned} s.t. ~~ \alpha_1t_1 + \alpha_2t_2 &= -\sum_{i=3}^N{\alpha_i t_i}=\zeta\\ 0 \le \alpha_1 &\le C\\ 0 \le \alpha_2 &\le C \end{aligned}$$

对于其中的等式约束，由于等式约束的右边是一个定值，这里直接使用一个变量$\zeta$来表示。

---

$t_1$和$t_2$异号

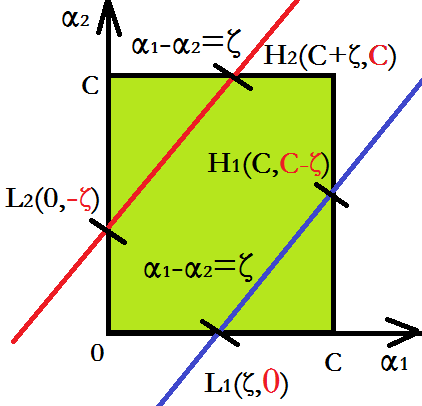
对于$t_1$和$t_2$异号的情况，用图形将上面这个约束表示出来就如下图所示：

首先，基于不等式约束：

$$\begin{aligned} 0 \le \alpha_1 &\le C\\ 0 \le \alpha_2 &\le C \end{aligned}$$

可以得到$\alpha_1,\alpha_2$ 只能在图中的绿色区域 $[0,C]\times[0,C]$ 内。

然后，由于$t_1$和$t_2$异号，不是一般性，这里直接考虑$t_1=1,t_2=-1$（如果反过来$t_1=-1,t_2=1$，也无所谓，只是$\alpha_1$和$\alpha_2$换一下变量的名字，对结果没影响）。那么，等式约束就是一条直线$\alpha_1-\alpha_2=\zeta$，即图中的红色和蓝色两条线中的一条，且该直线和对角线平行。

而等式约束和不等式约束的交集，就是图中绿色区域内的红色线段和蓝色线段。注意，最终的约束，都是线段，是绿色区域里面的 红色线段 和 蓝色线段。

因此，要求的是目标函数在一条平行于对消线的线段上的最优解，这就使得两个变量的最优解问题，转换成为了变量的优化问题（因为一旦一个变量定了，另一个也定了）。这里不妨假设，需要优化的变量为 $\alpha_2$ 。

这里假设问题的原始解为 $\alpha_1^{old},\alpha_2^{old}$，经过本次优化之后的最优解为 $\alpha_1^{new},\alpha_2^{new}$。由于优化变量为 $\alpha_2$ ，而 $\alpha_2^{old},\alpha_2^{new}$ 都必须满足上面这幅图，所以，可以从图中得到 $\alpha_2^{new}$ 的约束为为：

$$L \le \alpha_2^{new} \le H$$

这里 $L$ 是下界，其确定方式是上图中 $L_1、L_2$ 两个点，这两个点是约束线段的下端点，所以这两个点的 $\alpha_2$ 较大的一个要作为 $\alpha_2^{new}$ 的下界，也即是上图坐标中标红的数值：

$$L=max(0,-\zeta)=max(0,\alpha_2^{0ld}-\alpha_1^{old})$$

这里的 $H$ 是上界， 其确定方式是上图中 $H_1、H_2$ 两个点，这两个点是约束线段的上端点，所以这两个点的 $\alpha_2$ 较小的一个要作为 $\alpha_2^{new}$ 的上界，也即是上图坐标中标红的数值：

$$H=min(C,C-\zeta)=max(C,C+\alpha_2^{0ld}-\alpha_1^{old})$$

也就是说，此时 $\alpha_2^{new}$有了上面的新的约束。

---

$t_1$和$t_2$同号

当$t_1$和$t_2$同号的时候，等式约束为 $\alpha_1+\alpha_2=\zeta$，此时也是一条平行于对角线的直线，只是与$t_1$和$t_2$异号时方向垂直，其他的分析是一样的，这里就不再重复，原文中将中情况的图都做出出来：

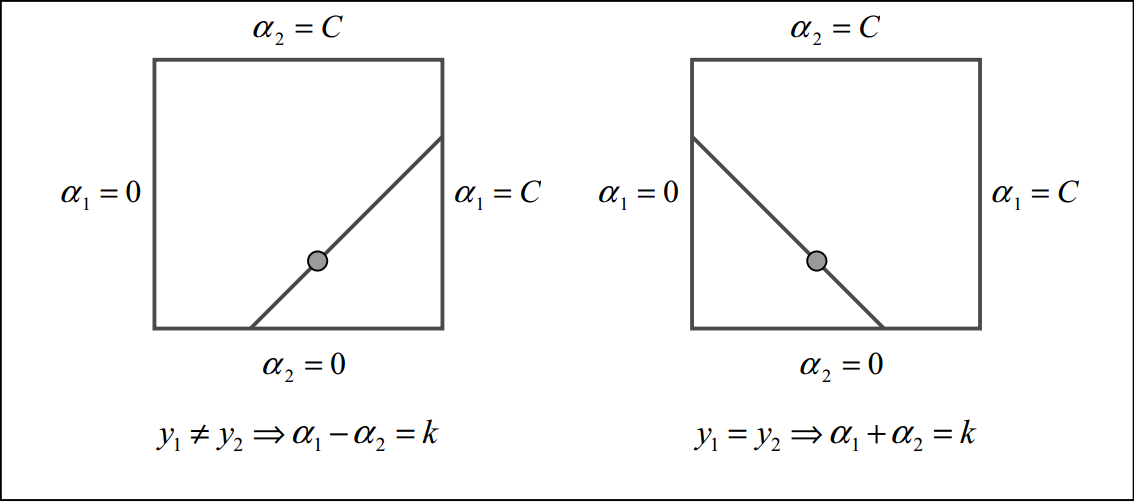
左图即 $t_1$和$t_2$异号的情况，右图是$t_1$和$t_2$同号的情况。

很容易得到，在$t_1$和$t_2$同号的时候有约束：

$$L \le \alpha_2^{new} \le H\\ L=max(0,\zeta-C)=max(0,\alpha_2^{0ld}+\alpha_1^{old}-C)\\ H=min(C,\zeta)=max(C,alpha_2^{0ld}+\alpha_1^{old})$$

---

优化结果

这里仅仅给出优化的结果，并不给出证明，具体证明可以参考《统计学习方法》。

目标函数沿着沿着对角线的二次导数可以表示为：

$$\eta=K(x_1,x_1)+K(x_2,x_2)-2K(x_1,x_2)$$

在一般的情况下，目标函数是正定的，那么，沿着等式约束必然有一个最小值，并且$\eta$必然大于0。在这种情况下，SMO算法沿着等式约束得到的最优解为：

$$\alpha_2^{new}=\alpha_2^{old}+\frac{E_1-E_2}{\eta}$$

由于$g(x)$在前面已经定义过，这里可以直接定义$E_i$为：

$$E_i=g(x_i)-t_i=\{\sum_{j=1}^N\{\alpha_j t_j K(x_j,x_i)\} + b\}-t_i$$

注意上面的下标，既有$i$，也有$j$。很容易看出，$E_i$ 是输出 $g(x_i)$ 对于输入 $x_i$ 的预测值和 $x_i$ 的真实值值 $t_i$之差。

由于上面仅仅考虑了等式约束，现在，将前面的结果加上不等式约束：

$$L \le \alpha_2^{new} \le H$$

那么，最终的 $\alpha_2^{new}$的结果为：

$$\alpha_2^{new,cliped}= \begin{cases} H& \text{ $\alpha_2^{new} > H$}\\ \alpha_2^{new}& \text{$L\le \alpha_2^{new} \le H$}\\ L& \text{$\alpha_2^{new}<L$} \end{cases}$$

这里的$cliped$是剪辑的意思，$\alpha_2^{new}$ 仅仅是线性约束得到的结果，但是并未经过 $L \le \alpha_2^{new} \le H$ 剪辑，所以将不等式约束之后的结果，成为剪辑之后的 $\alpha_2^{new}$，即：$\alpha_2^{new,cliped}$

在求得$\alpha_2^{new,cliped}$由等式约束，就可以很容易得到，$\alpha_1^{new}$的结果为：

$$\alpha_1^{new} = \alpha_1^{old} + t_1t_2(\alpha_1^{old}-\alpha_2^{new})$$

很容易看到，此时$\alpha_1$ 和 $\alpha_2$ 改变的量相同，但是方向相反。

这样就得到了 $\alpha_1^{new}$ 和 $\alpha_2^{new}$ 。

---

4.3 二变量拉格朗日乘子的选择

前面是先给出了 $\alpha_1$ 和 $\alpha_2$ 的优化方法，但是并未说明，算法中具体要选择哪 两个变量 做为$\alpha_1$ 和 $\alpha_2$ 来优化。这一节就详细的说明一下 $\alpha_1$ 和 $\alpha_2$ 的选择方法。

原文中，将这里的变量选择方法称为启发式（Heuristics ）算法。其基本思路是：
1. 因为KKT条件是最优解的充分必要条件，所以，如果所有变量的解都满足最优化问题的KKT条件，那么，这个最优化问题的解就得到了。
2. 如果KKT条件不满足，则选择两个变量，而固定其他变量，这对这两个选择的变量，构建一个二变量QP优化问题，这两个变量其中一个是违反KKT条件最严重的哪一个变量，另一个则是由约束条件自动选择的。

---

第一个变量的选择

SMO算法选择第一个变量，是选择违反KKT条件最严重的那个变量，这里的KKT条件就是：

$$\begin{aligned} \alpha_i=0 &\Leftrightarrow t_ig(x_i) \ge 1\\ 0<\alpha_i<C &\Leftrightarrow t_ig(x_i) = 1\\ \alpha_i=C &\Leftrightarrow t_ig(x_i) \le 1 \end{aligned}$$

其中：

$$g(x)=\sum_{i=1}^N\{\alpha_i t_i K(x_i,x_j)\} + b$$

将第一个变量的选择称为外层循环（outer loop），外层循环首先需要遍历整个训练样本，判断是否存在违反上述KKT条件的样本点。如果某个样本点 $x_i$ 违反了KKT条件，那么该样本点 $x_i$ 就有可能在下一步被优化。

在遍历过程中，外层循环首先遍历所有 $0<\alpha_i<C$ 的样本点，这些样本点代表的就是在margin边界上面的点。如果这里面的样本点违反了KKT条件，那么优先优化这些样本点。

如果 $0<\alpha_i<C$ 的样本点都满足KKT条件，那么在遍历整个训练样本集合，检验他们是否都满足KKT条件。

最终，是要根据上面的选择优先级，选出一个违反KKT条件最严重的样本点。

什么是违反KKT条件最严重的样本点？
答：举个例子，如果一个样本点满足 $0<\alpha_i<C$，那么根据KKT条件，其应该也满足 $t_ig(x_i) = 1$， 但是，如果它不满足后面这个等式的话，就说这个样本点违反了KKT条件。其严重程度，自然是定义为 $t_ig(x_i) - 1$ ，即数值上偏离的程度。

还有一点就是，由于KKT条件过于的严格，比如 $t_ig(x_i) = 1$ ，这个条件一般很难达到，所以在检验KKT条件的时候，都是在一定的误差限 $\epsilon$ 内检验KKT条件的， 即 $|t_ig(x_i) - 1| < \epsilon$。

上面就是对第一个变量的启发式选择方法。

---

第二个变量的选择

SMO算法对第二个变量的选择称为内层循环。这里，外层循环已经将第一个变量 $\alpha_1$ 找好了，现在需要在内层循环中，将第二个变量 $\alpha_2$ 找到。对第二个变量的选择所遵循的标准就是：$\alpha_2$ 的变化步长要尽量的大。

由于前面已经得到了：

$$\alpha_2^{new}=\alpha_2^{old}+\frac{E_1-E_2}{\eta}$$

为了使得 $\alpha_2$ 的步长足够的大，一种直观的选择方式就是选择能使得 $|E_1-E_2|$ 的 $\alpha_2$。

由于 $\alpha_1$ 在选择第一个变量的时候已经确定了，所以其对应的 $E_1$ 也确定了。

• 如果 $E_1$ 是一个正值，那么自然选择最小的 $E_i$ 作为 $E_2$ ，进而确定 $\alpha_2$
• 如果 $E_1$ 是一个负值，那么自然选择最大的 $E_i$ 作为 $E_2$ ，进而确定 $\alpha_2$

如果说，在某种特殊情况下，内层循环所选择的 $\alpha_2$ 并不能使得目标函数有足够的下降，则采用下面的启发式规则来继续选择 $\alpha_2$ : 遍历在间隔边界上的所有的支持向量点，依次将其作为 $\alpha_2$ 来使用。如果再这种情况下，目标函数仍然没有足够的下降的话，那么就放弃当前的 $\alpha_1$ 重新选择一个 $\alpha_1$ 来实现遍历的选择。

---

4.3 阈值计算

每次基于上面的变量选择和变量优化之后，都需要对阈值 $b$ 做一次更新。对 $b$ 的更新，自然是要找在margin边界上的点来更新是最方便的，即 $0<\alpha_1^{new}<C$ 的点。由此时的KKT条件：

$$t_ig(x_i) = 1$$

可以很容易知道：

$$t_i\{\sum_{i=1}^N\{\alpha_i t_i K(x_i,x_1)\} + b\}= 1$$

且$t_i^2=1$，进而有：

$$\sum_{i=1}^N\{\alpha_i t_i K(x_i,x_1)\} + b= t_1$$

所以：

$$b_1^{new}=t_1-\sum_{i=1}^N\{\alpha_i t_i K_{i1}\}-\alpha_1^{new}t_1K_{11}-\alpha_2^{new}t_2K_{21}$$

这里为了简化表达，定义$K_{ij}=K(x_i,x_j)$

又根据前面关于 $E_i$ 的定义可以知道:

$$E_i=g(x_i)-t_i=\{\sum_{j=1}^N\{\alpha_j t_j K_{ji}\} + b\}-t_i$$

拆开后有：

$$E_i=\{\sum_{i=3}^N\{\alpha_i t_i K_{i1}\} + \alpha_1^{old}t_1K_{11}+\alpha_2^{old}t_2K_{21}+ b^{old}\}-t_1$$

变换一下这个式子就可以得到：

$$t_1-\sum_{i=3}^N\{\alpha_i t_i K_{i1}\} = -E_1+ \alpha_1^{old}t_1K_{11}+\alpha_2^{old}t_2K_{21}+ b^{old}$$

将上面这个式子带入到$b_1^{new}$中，就可以得到：

$$b_1^{new}=-E_1-t_1K_{11}(\alpha_1^{new}-\alpha_1^{old})-t_2K_{21}(\alpha_2^{new}-\alpha_2^{old}) + b^{old}$$

同样的计算方式，可以得到，当 $0<\alpha_2^{new}<C$ 时，有：

$$b_2^{new}=-E_2-t_1K_{12}(\alpha_1^{new}-\alpha_1^{old})-t_2K_{22}(\alpha_2^{new}-\alpha_2^{old}) + b^{old}$$

如果 $\alpha_1^{new},\alpha_2^{new}$ 同时满足 $0<\alpha_i^{new}<C$ ，那么：

$$b^{new}=b_1^{new}=b_2^{new}$$

否通则的话：

$$b^{new}=\frac{b_1^{new}+b_2^{new}}{2}$$