感知机（Perceptron）

监督学习

---

@ author ： duanxxnj@163.com
@ time : 2016-11-05

---

感知机简介

前面一篇文章是关于 $logistic Regresion$ 回归的，其中提到LR回归是一个判别式模型。这里再研究另一个判别式模型：感知机。感知机模型在机器学习中有举足轻重的地位，它是SVM和神经网络的基础。

总的来说，感知机是机器学习、数据挖掘、神经网络、深度学习等当前计算机行业热门研究方向的基础。

之前的线性回归的概率解释中，假设样本的概率密度函数的参数形式是已知的，然后需要基于样本，使用参数估计的方法来估计概率密度函数的参数值；这里的感知机算法和前一篇文章《LR回归》，都是直接假设 判别函数的参数形式是已知的 ，然后基于训练样本，使用某种学习算法，来学习判别函数的参数值，被称为判别式方法，感知机所得到的是一个线性判别函数。而一般来说，寻找线性判别函数的问题，会被形式化为极小化准则函数的问题，以分类为目的的准则函数可以是样本的风险函数，或者是训练误差。

感知器的最初概念可以追溯到Warren McCulloch和Walter Pitts在1943年的研究Warren McCulloch和Walter Pitts在1943年的研究，他们将生物神经元类比成带有二值输出的简单逻辑门。以更直观的方式来看，神经元可被理解为生物大脑中神经网络的子节点。在这里，变量信号抵达树突。输入信号在神经细胞体内聚集，当聚集的信号强度超过一定的阈值，就会产生一个输出信号，并被树突传递下去。

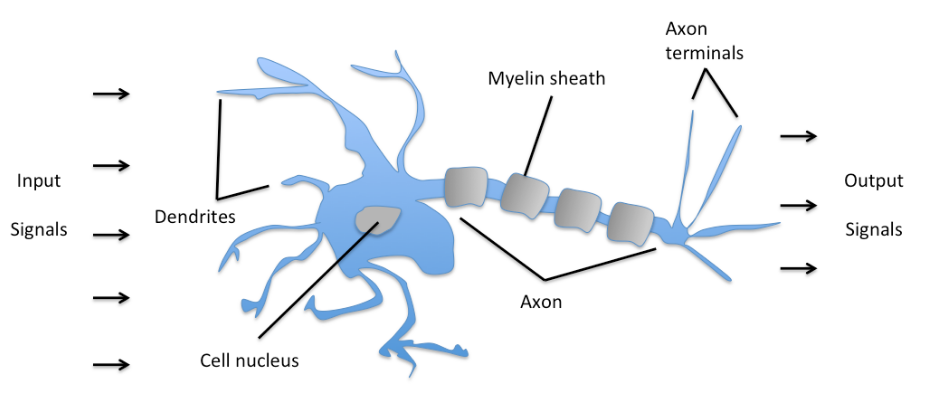
后来，Frank Rosenblatt 1957年发表了一篇论文《The perceptron, a perceiving and recognizing automaton Project Para》。这篇文章最大的贡献就是基于神经元定义了感知机算法的概念。并说明了，感知机算法的目的，就是针对多维特征的样本集合，学习一个权值向量 $w$，使得 $w$ 乘以输入特征向量 $x$ 之后，基于乘积，可以判断一个神经元是否被激活。
-----------------

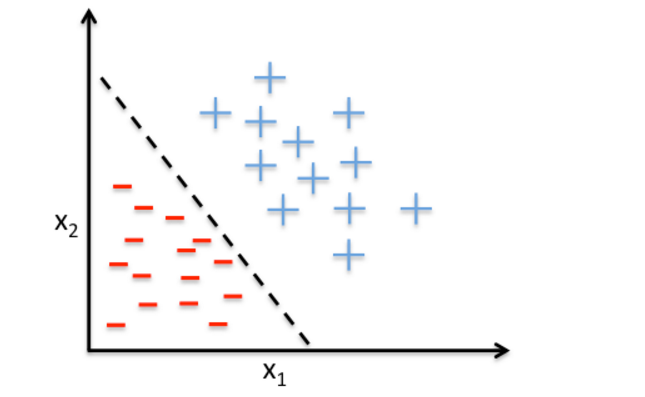
从机器学习的角度来讲，感知机属于监督学习（supervised learning），它是一个单层的二分类器。

广义线性模型下的感知机

感知机模型是一个二分类模型，和线性回归模型一样，感知机模型一般会使用一些特征函数$\phi(x)$，将输入空间映射到新的特征空间中，再进行计算。感知机模型对应于特征空间中将实例划分为正负两类的分离超平面，故而是判别式模型。感知机模型的数学表达式如下:

$$y(x)=f(w^T\phi(x))=w_0\phi(x_0)+w_1\phi(x_1)+...+w_n\phi(x_n)$$

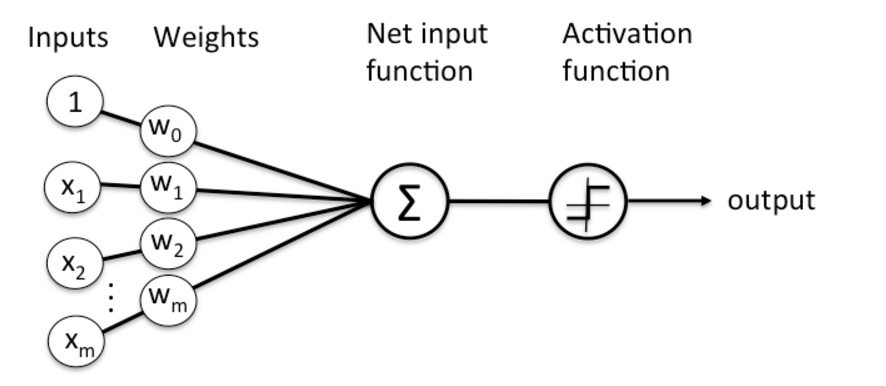
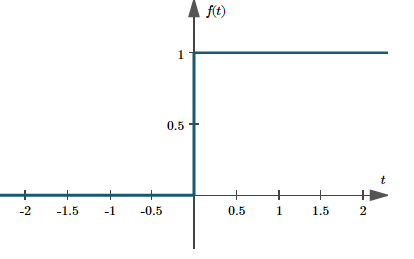
这里$f(\cdot)$ 叫做激活函数(Activation function)：

$$f(a)= \begin{cases} +1& \text{a$\ge$0}\\ -1& \text{a<0} \end{cases}$$

有时也被称为单位阶跃函数（Unit Step Function）:
-------------------------------

在LR模型中，输出的取值为 $t\in\{1,0\}$ ，在感知机模型中，输出的取值为 $t\in\{+1,-1\}$ 。

感知机算法相对来说，十分的简单，其分可以分为原始形式和对偶形式。

模型有了，现在要考虑其损失函数的形式，由于感知机模型的输出是0和1两个离散的值，如果使用基于分类错误的平方误差，会使得损失函数不连续，更别说是否可导了。所以这里使用下面这个损失函数，在后面将$SVM$的时候就可以知道，这个损失函数其实就是$SVM$中的函数间隔：

$$E=-\sum_{n\in M}{w^T\phi(x_n)t_n}$$

其中，$M$是分类错误的样本子集；$\phi(x)$是输入变量$x$的特征提取函数，一般来说，我们用$x$指代输入空间，但是，在实际的问题中，输入空间的变量很难直接用于模型学习，需要在输入空间的基础上再做一个特征变换的操作$\phi(x)$，将输入空间变换到特征空间，然后用特征空间进行模型的学习。

损失函数，针对的是分类错误的样本子集！！！
损失函数，针对的是分类错误的样本子集！！！
损失函数，针对的是分类错误的样本子集！！！
重要的事情说三遍

对于上面的损失函数而言：
当 $t_n=+1$的时候，由于样本被分类错误， $w^T\phi(x_n)<0$，所以 $-w^T\phi(x_n)t_n>0$
当 $t_n=-1$的时候，由于样本被分类错误， $w^T\phi(x_n)>0$，所以 $-w^T\phi(x_n)t_n>0$

故而这里$E$始终为正值，损失函数 $E$ 越小，那么模型被模型分类错误的样本点就越少，模型的正确率也就越高，当$E$取其最小值 0 的时候，感知机模型就可以将输入样本完全的分开。

所以，感知机模型的学习问题，最终成为了损失函数最小化的问题。

当然，这里需要注意一个特殊情况: 如果样本点刚好落在了决策超平面上，那么$w^T\phi(x_n)=0$，这种情况，无论将这个样本点判给哪个类，都无所谓，可以不予考虑。

---

由于损失函数 $E$ 是一个凸函数，所以损失函数 $E$ 最小化的问题，可以直接使用梯度下降法来求解，过程如下：

首先对损失函数求梯度：

$$\nabla E(w)=-\sum_{n\in M}{\phi(x_n)t_n}$$

和线性回归模型一样，有了梯度之后，就可以使用梯度下降法来求解模型的参数了：

$$w_{t+1}=w_{t}-\eta_t \nabla E(w)=w_t + \eta_t \sum_{n\in M}{\phi(x_n)t_n}$$

这种算法也叫作批处理算法（batch algorithm），使用“批处理”这个术语，主要是因为每次在修正权值向量的时候（也就是这个过程：$w_{t+1}=w_{t}-\eta_t \nabla E(w)$），都需要计算成批的样本，就是说，上面这个方法，每次迭代的时候，都需要遍历整个训练集合，所以称为批处理。

与之相对的就是下面的随机梯度下降法，这是一种单样本方法，或者叫做在线学习算法（online algorithm），这种算法的计算复杂度会低很多。

参照上面批处理的权值更新公式，将其中的求和运算符去掉，这里的$n$是在$M$中随机选择的一个，所以称为随机梯度下降法:

$$w_{t+1}=w_t + \eta_t {\phi(x_n)t_n};其中n\in M$$

无论是批处理梯度下降法还是随机梯度下降法，式中的 $\eta_t$ 都需要满足：

$$\sum_{k=1}^{\infty}\eta_{k}\to\infty \\ \sum_{k=1}^{\infty}\eta_{k}^2 < \infty$$

最常见的一个满足上述两个条件的函数为：$\eta_{k}=\frac{1}{k}$。在很多的教科书上，都会将$\eta_{k}$取为一个定值，这个是可行的，不过需要你给出一个合适的值，否则的话，算法的性能会比较的差，并且很容易出现在最优解附近震荡的现象。

感知机代码实现

代码连接

#-*- coding=utf-8 -*-
"""
@file ： perceptron.py
@author : duanxxnj@163.com
@time : 2016/11/5 19:56
"""
import time
import numpy as np
import random
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
"""
    感知机算法实现
"""
class Perceptron(object):
    """
        n_iter 是感知机算法的迭代次数
        eta 是感知机算法权值更新的系数，这个系数越小，更新步长越小
    """
    def __init__(self, n_iter=1, eta=0.01):
        self.n_iter = n_iter
        self.eta = eta
    """
        感知机算法学习函数，这个函数学习感知机的权值向量W
        X   [n_samples, n_features]二维向量，数据样本集合，其第一列全部为1
        y   [n_samples]以为向量，数据的标签，这里为[+1,-1]
        fun 感知机所使用的优化函数：“batch”：批处理梯度下降法
                                “SGD”：随机梯度下降法
        isshow 是否将中间过程绘图出来：False ：不绘图
                                   True : 绘图
    """
    def fit(self, X, y, fun="batch",isshow=False):
        n_samples, n_features = X.shape #获得数据样本的大小
        self.w = np.ones(n_features, dtype=np.float64) #参数W
        if isshow == True:
            plt.ion()
        # 如果是批处理梯度下降法
        if fun == "batch":
            for t in range(self.n_iter):
                error_counter = 0
                # 对分类错误的样本点集合做权值跟新更新
                for i in range(n_samples):
                    if self.predict(X[i])[0] != y[i]:
                        # 权值跟新系数为 eta/n_iter
                        self.w += y[i] * X[i] * self.eta/self.n_iter
                        error_counter = error_counter +1
                if (isshow):
                    self.plot_process(X)
                # 如果说分类错误的样本点的个数为0，说明模型已经训练好了
                if error_counter == 0:
                    break;
        # 如果是随机梯度下降法
        elif fun == "SGD":
            for t in range(self.n_iter):
                # 每次随机选取一个样本来更新权值
                i = random.randint(0, n_samples-1)
                if self.predict(X[i])[0] != y[i]:
                    # 为了方便这里的权值系数直接使用的是eta而不是eta/n_iter
                    # 并不影响结果
                    self.w += y[i] * X[i] * self.eta
                if (t%10 == 0 and isshow):
                    self.plot_process(X)
                # 此处本应该加上判断模型是否训练完成的代码，但无所谓
    """
        预测样本类别
        X   [n_samples, n_features]二维向量，数据样本集合，其第一列全部为1
        return 样本类别[+1, -1]
    """
    def predict(self, X):
        X = np.atleast_2d(X)#如果是一维向量，转换为二维向量
        return np.sign(np.dot(X, self.w))
    """
        绘图函数
    """
    def plot_process(self, X):
        fig = plt.figure()
        fig.clear()
        # 绘制样本点分布
        plt.scatter(X[0:50, 1], X[0:50, 2], c='r')
        plt.scatter(X[50:100, 1], X[50:100, 2], c='b')
        # 绘制决策面
        xx = np.arange(X[:, 1].min(), X[:, 1].max(), 0.1)
        yy = -(xx * self.w[1] / self.w[2]) - self.w[0] / self.w[2]
        plt.plot(xx, yy)
        plt.grid()
        plt.pause(1.5)
if __name__ == '__main__':
    # 加载数据
    iris_data = load_iris()
    y = np.sign(iris_data.target[0:100] - 0.5)
    X = iris_data.data[0:100, [0, 3]]
    X = np.c_[(np.array([1] * X.shape[0])).T, X]
    # 选择算法输入1/2
    choose = input("choose batch or SGD(1/2):")
    if choose == 1:
        clf = Perceptron(15, 0.03)
        clf.fit(X, y, "batch", True)
    elif choose == 2:
        clf = Perceptron(200, 0.1)
        clf.fit(X, y, "SGD", True)

---

感知机的原始形式 和 对偶形式

以上就是广义线性模型下的感知机模型，这个是感知机模型的原始形式，感知机模型最重要的并不是它的原始形式，而是他的对偶形式，这个里的对偶形式就是$SVM$求解中对偶形式的原型，很好的理解了感知机的对偶形式，那么$SVM$的对偶形式就可以很好的理解了。

每一个线性规划问题，我们称之为原始问题，都有一个与之对应的线性规划问题我们称之为对偶问题。原始问题与对偶问题的解是对应的，得出一个问题的解，另一个问题的解也就得到了。并且原始问题与对偶问题在形式上存在很简单的对应关系：
- 目标函数对原始问题是极大化，对偶问题则是极小化
- 原始问题目标函数中的系数，是对偶问题约束不等式中的右端常数，而原始问题约束不等式中的右端常数，则是对偶问题中目标函数的系数
- 原始问题和对偶问题的约束不等式的符号方向相反
- 原始问题约束不等式系数矩阵转置后，即为对偶问题的约束不等式的系数矩阵
- 原始问题的约束方程数对应于对偶问题的变量数，而原始问题的变量数对应于对偶问题的约束方程数
- 对偶问题的对偶问题是原始问题

感知机原始形式

这里为了和后面的$SVM$以及神经网络在公式上相对应，对上面感知机的原始形式做一个重写：

给定一个数据集：$T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$，其中$y_i\in \{+1, -1\}$，将广义线性模型下的损失函数：

$$E=-\sum_{n\in M}{w^T\phi(x_n)t_n}$$

重写为：

$$E=-\sum_{x_i\in M}{(w^Tx_i+b)y_i}$$

其中$b$一般被称为偏置。

那么损失函数的梯度就可以写为:

$$\nabla_w E(w,b)=-\sum_{x_i\in M}{x_iy_i}\\ \nabla_b E(w,b)=-\sum_{x_i\in M}{y_i}$$

其对应的梯度下降法的参数更新方法为：

$$w_{t+1}=w_{t}-\eta_t \nabla_w E(w,b)=w_t + \eta_t \sum_{n\in M}{x_iy_i}\\ b_{t+1}=b_{t}-\eta_t \nabla_b E(w,b)=b_t + \eta_t \sum_{n\in M}{y_i}$$

其对应的随机梯度下降法的参数更新方法为：

$$w_{t+1}=w_t + \eta_t {x_iy_i}\\ b_{t+1}=b_t + \eta_t {y_i}$$

其中$x_i \in M$，$\eta_t$需要满足的限制条件和前面的一样：

$$\sum_{k=1}^{\infty}\eta_{k}\to\infty \\ \sum_{k=1}^{\infty}\eta_{k}^2 < \infty$$

感知机随机梯度下降法的直观解释：对于感知机而言，当一个样本点被误分类之后，被误分类的样本点会位于决策超平面的错误的一侧，这时感知机会调整$w,b$的值，使决策超平面向该误分类点的一侧移动，移动的尺度由$\eta_t$决定，每一次移动，都可以减少误分类点和决策超平面之间的距离，直到决策超平面越过该误分类点，使其被正确分类为止。

对于一个线性可分的数据集而言，感知机经过有限次搜索之后，一定可以找到将训练数据完全正确分开的决策超平面。也就是说，但训练数据集是线性可分的时候，感知机学习算法的原始形式一定是迭代收敛的。

但是，同时需要注意：感知机学习算法存在许多的解，这些解即和感知机初值的选择有关，同时也依赖于迭代过程中随机选择的错误点的选择方法。

为了使得感知机可以有一个确定的最优解，就需要为感知机加上一些约束条件，这就是后面要讲的$SVM$的基本思想。

当训练的数据集线性不可分时，一般的感知机学习算法并不能迭代收敛，其结果会不断的震荡，这个问题在$SVM$中使用软间隔最大化来解决的。

感知机的对偶形式

感知机算法的对偶式，是针对感知机随机梯度下降法来设计的。其基本思想是：感知机的原始式中，$x$ 是自变量，$y$ 是因变量，$w,b$ 是模型的参数，通俗点说，在感知机的原始算法中，是用参数$w,b$来表示$y$和$x$的。对偶式就是要把这这个关系反过来，用样本$x$和$y$的线性组合来表示参数$w$和$b$。

感知机随机梯度下降法的参数更新方式为:

$$w_{t+1}=w_t + \eta_t {x_iy_i}\\ b_{t+1}=b_t + \eta_t {y_i}$$

对于第$i$个样本，每次其被分类错误，都会有一次基于$x_i,y_i$的权值跟新，那么假设，到最后，整个感知机算法更新结束时，第$i$个样本点总共更新了$n_i$次。这样就不难得到，最后学习到的$w,b$分别为：

$$w=\sum_{i=1}^N{n_i \eta_{n_i} y_i x_i}\\ b=\sum_{i=1}^N{n_i \eta_{n_i} y_i}$$

在感知机原始形式中，$\eta_{t}$和迭代次数 $t$ 相关，在对偶形式中，$\eta_{n_i}$是和对应的样本点的权值更新次数$n_i$相关。当然，这里的$\eta_{n_i}$也必须满足：

$$\sum_{k=1}^{\infty}\eta_{k}\to\infty \\ \sum_{k=1}^{\infty}\eta_{k}^2 < \infty$$

很容易知道，$n_i$越大，说明对应的第$i$个样本点更细你的次数就越多，也就意味着这个样本点距离分类超平面越近，其正确分类的难度也就越大，那么，这个点对于模型的影响也就越大。在$SVM$中，这种点，很有可能就是支持向量。

故而，感知机模型的对偶形式的模型为：

$$y(x)=f(w^Tx+b)=f(\{\sum_{j=1}^N{n_j \eta_{n_j} y_j x_j}\}*x + \sum_{j=1}^N{n_j \eta_{n_j} y_j})$$

这里$f(\cdot)$ 叫做激活函数：

$$f(a)= \begin{cases} 0& \text{a$\ge$0}\\ 1& \text{a<0} \end{cases}$$

注意，上式中，为了和样本点$(x_i,y_i)$的下标 $i$ 相区别开来，这里选用的下标是 $j$ 。

其训练过程为：
在训练集中选取一个样本点$(x_i,y_i)$，如果该点分类错误，那么该点的权值更新加一次：

$$y_i(\{\sum_{j=1}^N{n_j \eta_{n_j} y_j x_j}\}*x_i + \sum_{j=1}^N{n_j \eta_{n_j} y_j}) \le 0$$

那么，更新公式为( 注意，这里的下标是 $i$ ):

$$n_i=n_i+1$$

这个其实就是想说，在$N$个训练样本依次循环的输入到算法中，如果对于某个样本分类错误，那么算法就对该样本点做一次更新。循环上面这个过程，直到所有的样本点都能够分类正确。

感知机对偶形式中的內积

在感知机对偶式的训练过程中，也就是下面这个公式中：

$$y_i(\{\sum_{j=1}^N{n_j \eta_{n_j} y_j x_j}\}*x_i + \sum_{j=1}^N{n_j \eta_{n_j} y_j}) \le 0$$

上面这个式子可以写成下面这个形式：

$$y_i(\sum_{j=1}^N{n_j \eta_{n_j} y_j （x_j*x_i）} + \sum_{j=1}^N{n_j \eta_{n_j} y_j}) \le 0$$

这里$（x_j*x_i）$ 表明，样本点的特征向量是以內积的形式存在于感知机对偶形式的训练算法中。为了简化计算过程，可以将训练集合之间的內积提前求出来，然后在训练过程中直接调用，样本点间的內积矩阵也就是所谓的Gram举证。

$$G=[x_i,x_j]_{N*N}$$

这里的內积，是$SVM$算法中核方法的原型，也是$SVM$之所以强大的根本原因。

感知机模型的袋式算法

感知机算法收敛的一个基本条件就是：样本是线性可分的。如果这个条件不成立的话，那么感知机算法就无法收敛。为了在样本线性不可分的情况下，感知机也可以收敛于一个相对理想的解，这里提出感知机袋式算法（Pocket algorithm）。

这个算法分为两个步骤：
1. 随机的初始化权值向量 $w_0$ , 定义一个存储权值向量的袋子 $P$，并为这个袋子设计一个计数器 $P_c$，计数器初始化为0。
2. 在第$t$次迭代的时候，根据感知机算法计算出其更新的权值$w_{t+1}$。用更新后的权值$w_{t+1}$测试分类的效果，分类正确的样本数为$h$，如果$h>P_c$，那么用$w_{t+1}$代替$w_t$，并更新 $P_c=h$。否则放弃当前更新。