@yangfch3
2016-01-20T04:54:44.000000Z
字数 4733
阅读 6111
线性代数
化学
行列式的性质
性质1 行列式与它的转置行列式相等.
性质2 互换行列式的两行(列),行列式变号.
推论 如果行列式有两行(列)完全相同,则此行列式为零.
性质3 行列式的某一行(列)中所有的元素都乘以同一数k,等于用数k乘此行列式.
推论 行列式的某一行(列)中所有元素的公因子可以提到行列式符号的外面.
性质4 行列式中如果有两行(列)元素成比例,则此行列式为零.
性质5 若行列式的某一列(行)的元素都是两数之和,例如:
则D等于下列两个行列式之和:
性质6 把行列式的某一列(行)的各元素乘以同一数然后加到另一列(行)对应的元素上去,行列式不变.
二阶、三阶行列式的运算
对角线法则:主对角线-副对角线
高阶行列式运算
定义法求解
行列式有多少项:全排列
每一项前面的正负号:逆序数(某个数的前面比它大的数的个数)
偶排列(+) 基排列(-)
对换相邻两个元素,排列改变奇偶性.变换法求解:三角型行列式
展开法求解:代数余子式
余子式 在n阶行列式中,把元素所在的第i行和第j列划去后,留下来的n-1阶行列式叫做元素的余子式,记作.
代数余子式
行列式等于它的
任一行(列)的各元素与其对应的代数余子式乘积之和,即
引理 一个n阶行列式,如果其中第i行所有元素除外都为零,那末这行列式等于 与它的代数余子式的乘积,即
线性方程组求解
线性方程组解的判据
(其中,A为系数矩阵,B为增广矩阵,R为矩阵的秩,n为未知数的个数)消元法
克莱姆法则
矩阵的运算
- 加减法
- 数乘
- 矩阵乘矩阵
- 转置矩阵
- 伴随矩阵
行列式的各个元素的代数余子式所构成的矩阵的转置,称为矩阵的伴随矩阵,记作. - 对称矩阵
逆矩阵
逆矩阵的性质
利用代数余子式求逆阵
- 待定系数法求逆阵
- 消元法求逆阵
- 求方程

- 求逆阵
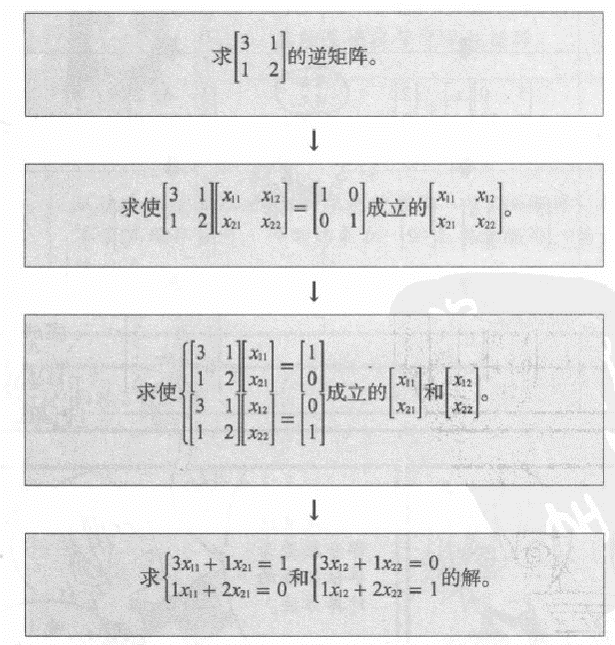
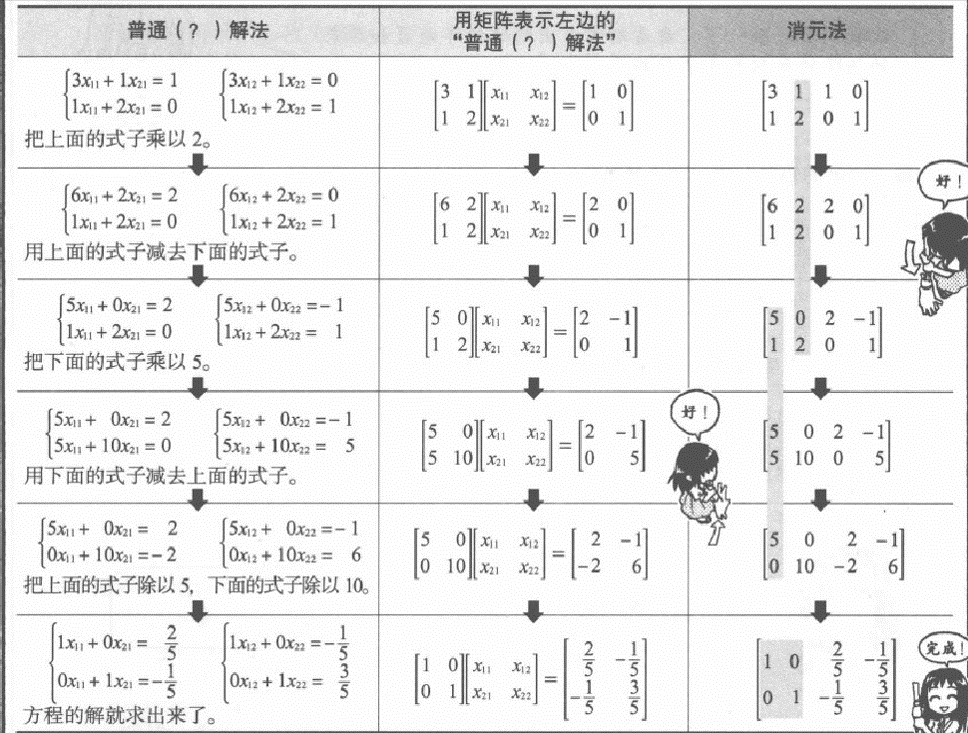
- 求方程
- 初等变换法
矩阵的初等变换
- 定义
- 对调两行(列);
- 以数乘某一行(列)的所有元素;
- 把某一行(列)所有元素的k倍加到另一行(列)对应的元素上去.
初等矩阵
由单位矩阵经过一次初等变换得到的方阵称为初等矩阵.初等变换
例如:
其中和都称为行阶梯形矩阵- 可划出一条阶梯线,线的下方全为零;
- 每个台阶只有一行,台阶数是非零行数;
- 对于任何矩阵总可经过有限次初等行变换得到行阶梯形和行最简形.
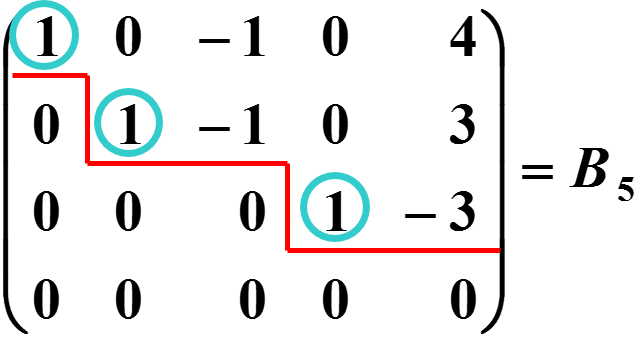
还称为行最简形矩阵,非零行的第一个非零元为1.
再经过列变换得到,称为的标准形.
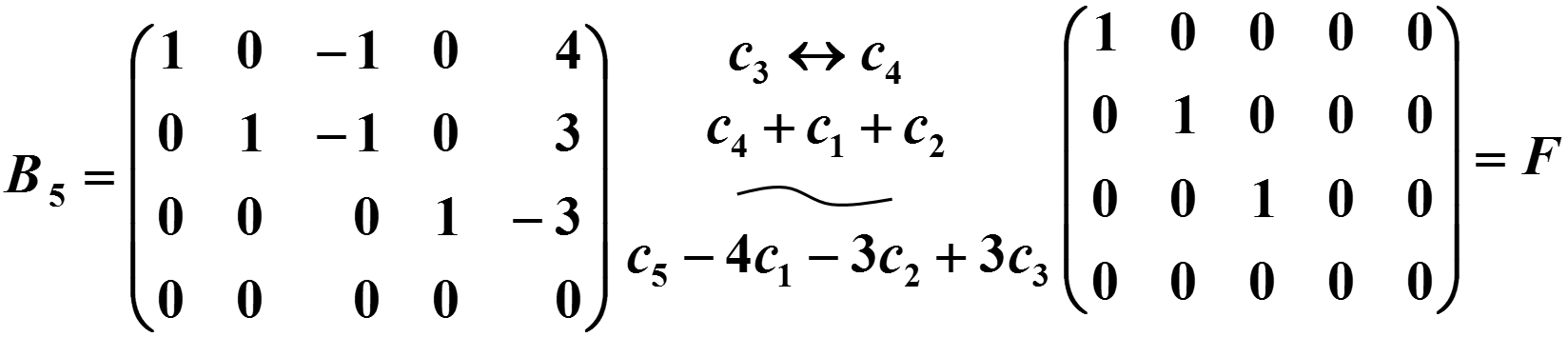

矩阵的秩
矩阵中不为零的子式的最大阶数,叫做的秩。
秩的用处:
- 向量的线性相关性-哪些向量相互表示;
- 方程组解的形式-多少个通解;
- 环境中独立的自由变量.
秩的性质:
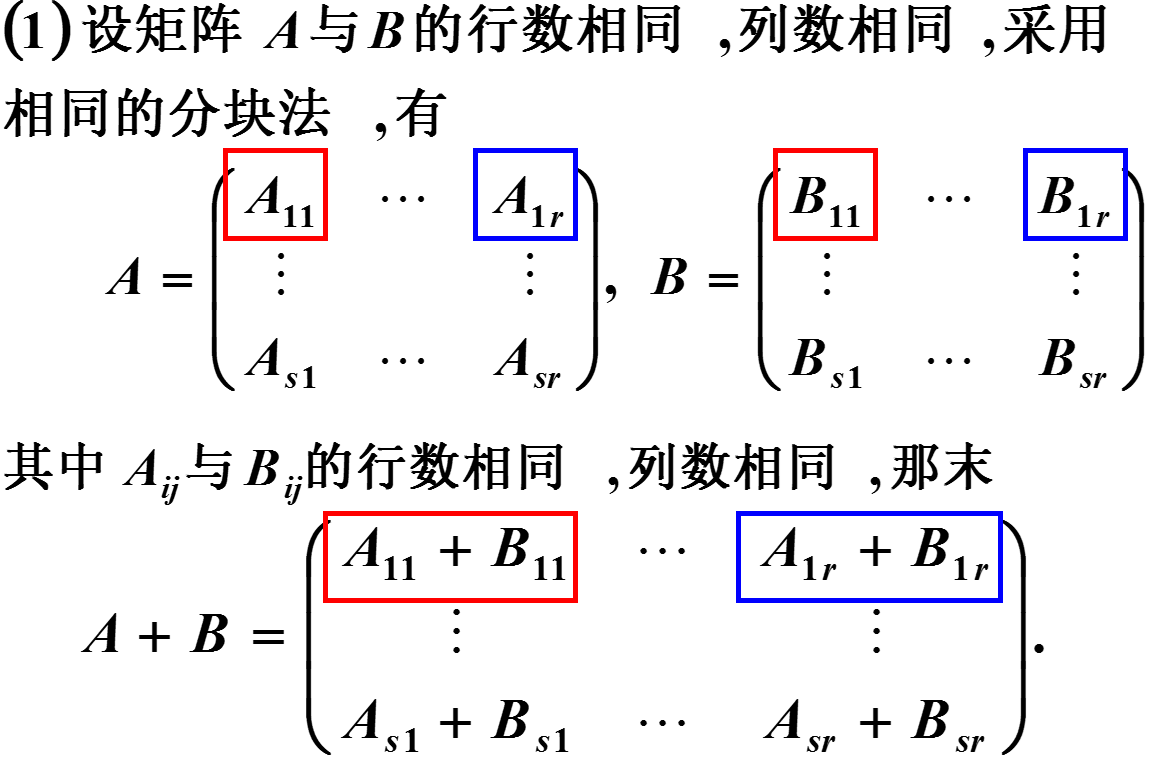
矩阵的分块
定义
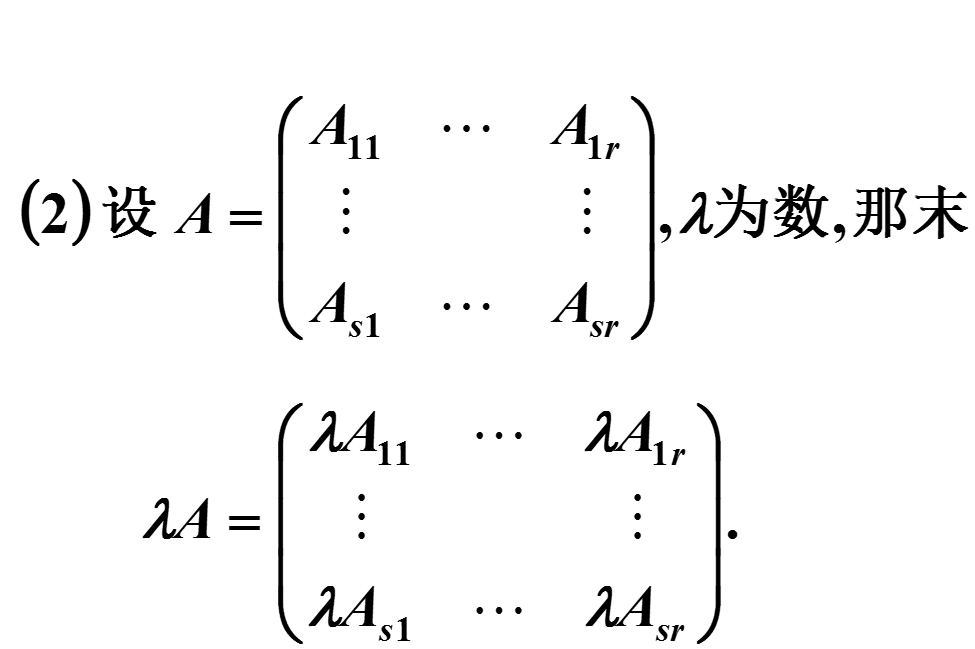
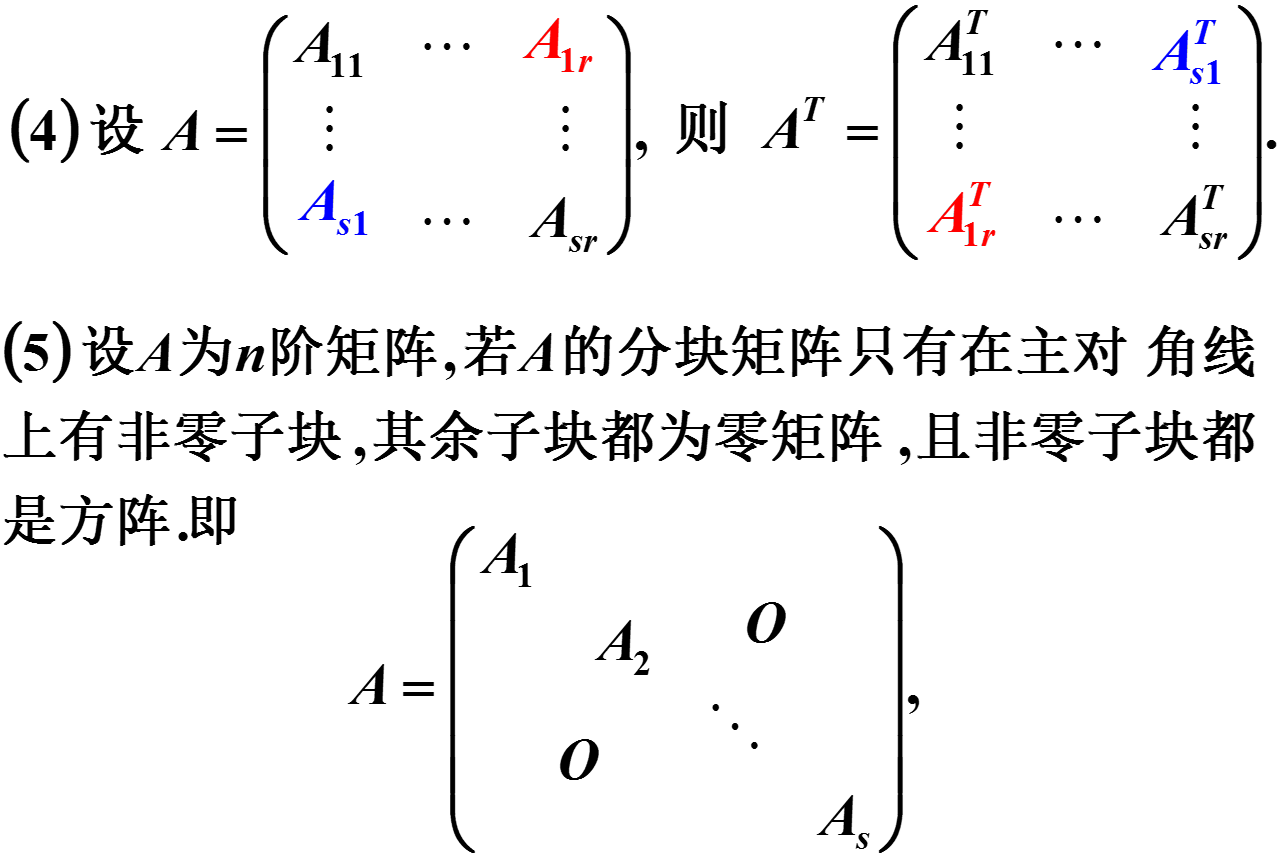
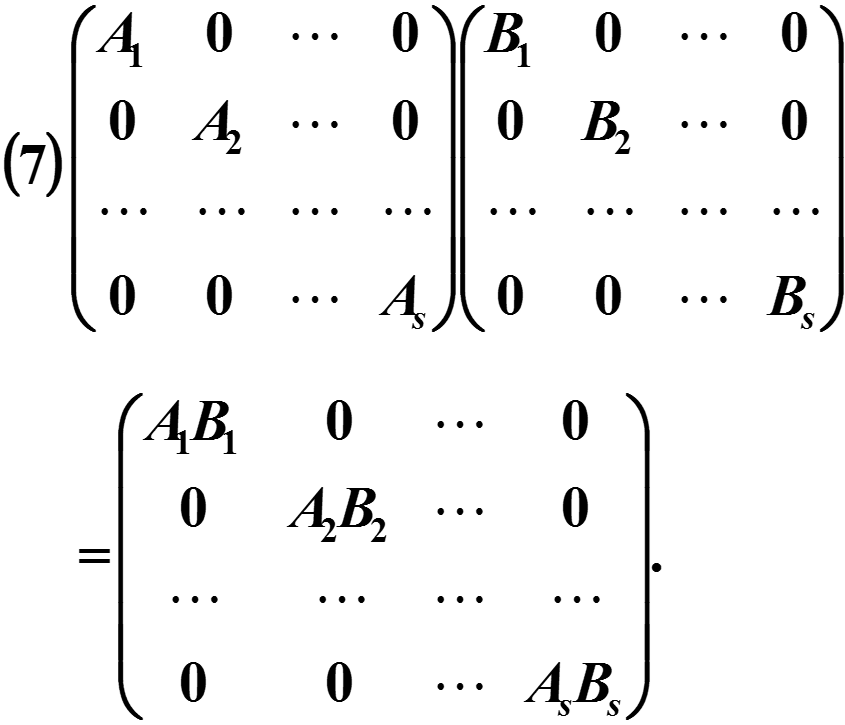
将矩阵用若干条纵线和横线分成许多个小矩阵,每一个小矩阵称为的子块,以子块为元素的形式上的矩阵称为分块矩阵.分块矩阵的运算