图数据库跟传统数据库以及图算法

cayley 图数据库

为什么需要图数据库

• SQL依然是表哥数据的最好存储方式
• s键值key-value依然是拓展性和速度上最快的
• 图数据库只是为我们提供了查询图状数据结构的一种方式

为什么图状的数据结构的查询会对我们那么有用呢？
因为可以使用图状数据结构来表示人类可以直观理解的个体与个体之间的联系

但是为什么都使用其他的数据存储方式呢？

图数据库可以给你带来几样关键的好处

1. 可以更简单地表示更复杂的数据
2. 可以更灵活地改变你要存储的关系 SQL都是需要预先定义模式的 所以当关系不断变化的时候 SQL相比图数据库的劣势就出来了
3. 可以更易于自定义关系 两个节点之间的关系想怎么定义就怎么定义
   4.可以支持一些设计图计算的算法 例如克鲁斯卡尔还有计算机网络的路由选路上涉及的一些算法

后面好像就没讲什么了 都是讲一些cayley图数据库的一些基础跟查询相关的 没有我想要的一些设计原理和并发处理的一些内容

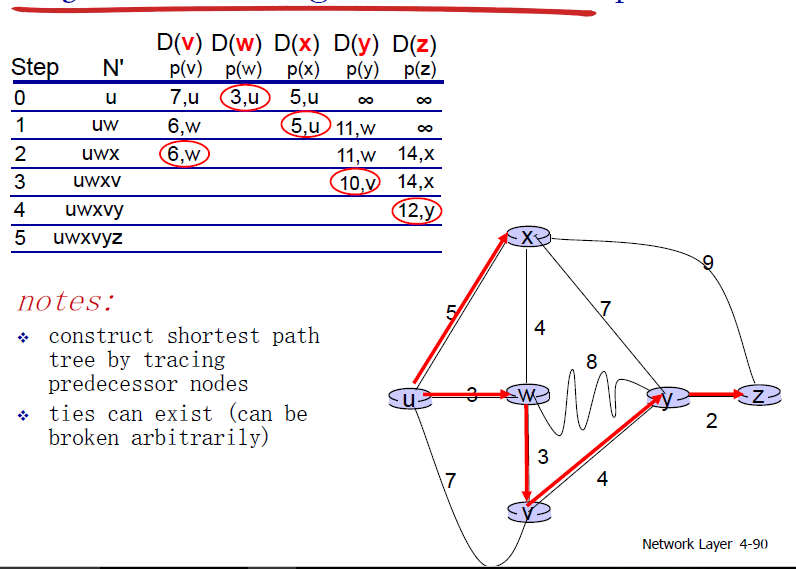
戴克斯克拉算法

全局地寻找一个点到每个点的最短路径

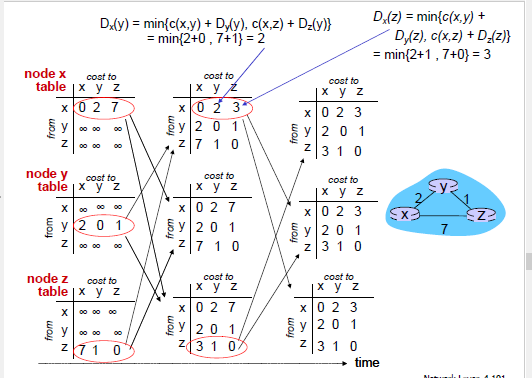
距离向量算法

表示：
dx(y)x到y整条路径的最小cost

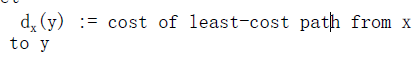
x到y的路径的cost等于它先到邻居的cost加上邻居到y的最小cost

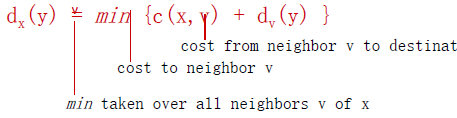
Bellman-Ford例子：

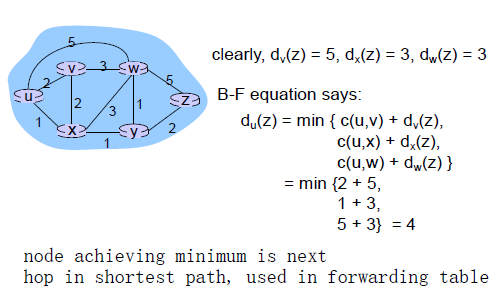
要点：
Dx(y)是x到y的最小cost估计，N中每个节点都需要估计自己到y节点的最小cost。

每个节点中有一个距离向量
Dx = [Dx(y): y є N ]
这个距离向量包含着这个节点到N中所有节点最小cost的估计

而对于每个节点的邻居节点，也是这样：
Dv = [Dv(y): y є N ]

在距离向量算法下，每个节点需要维护的信息有：

• 这个节点到邻居节点的cost
• 这个节点到N中每个节点的预计最小cost，也就是距离向量
• 这个节点邻居的距离向量

算法：

• 每段时间按之后，每个节点把自己的距离向量副本发送给自己的邻居
• 当每个节点接收到邻居发送过来的距离向量，拿这个距离向量更新自己的DV，使用BF公式

DV算法例子： 注意每个节点定时需要更新和把它的距离向量广播给它的邻居

LS和DV比较

• LS需要知道达到所有节点的cost，因此需要洪泛，但是DV不需要
• LS的时间复杂度是O(N^2)，时间复杂度比DV更高

最小生成树

最小生成树就是给一个图给你 每个点都是可以互相联通的 但是每条边的权重是不一样的 需要找出一堆边 使得这些点都连接起来 但是都不构成环 而且这些权重架起来还是最小

最小生成树一个很常见的应用场景是 城市之间需要铺电缆 每个城市之间都是可以铺的 但是不同城市之间铺设电缆的成本不一样 那么就需要我们找出一个满足要求的最小生成树 来让成本最低

找最小生成树的方法 一般有Kruskal克鲁斯卡尔算法

步骤

1. 新建图G，G中拥有原图中相同的节点，但没有边
2. 将原图中所有的边按权值从小到大排序
3. 从权值最小的边开始，如果这条边连接的两个节点于图G中不在同一个连通分量中，则添加这条边到图G中
4. 重复3，直至图G中所有的节点都在同一个连通分量中

维基百科上给的例子 非常容易理解

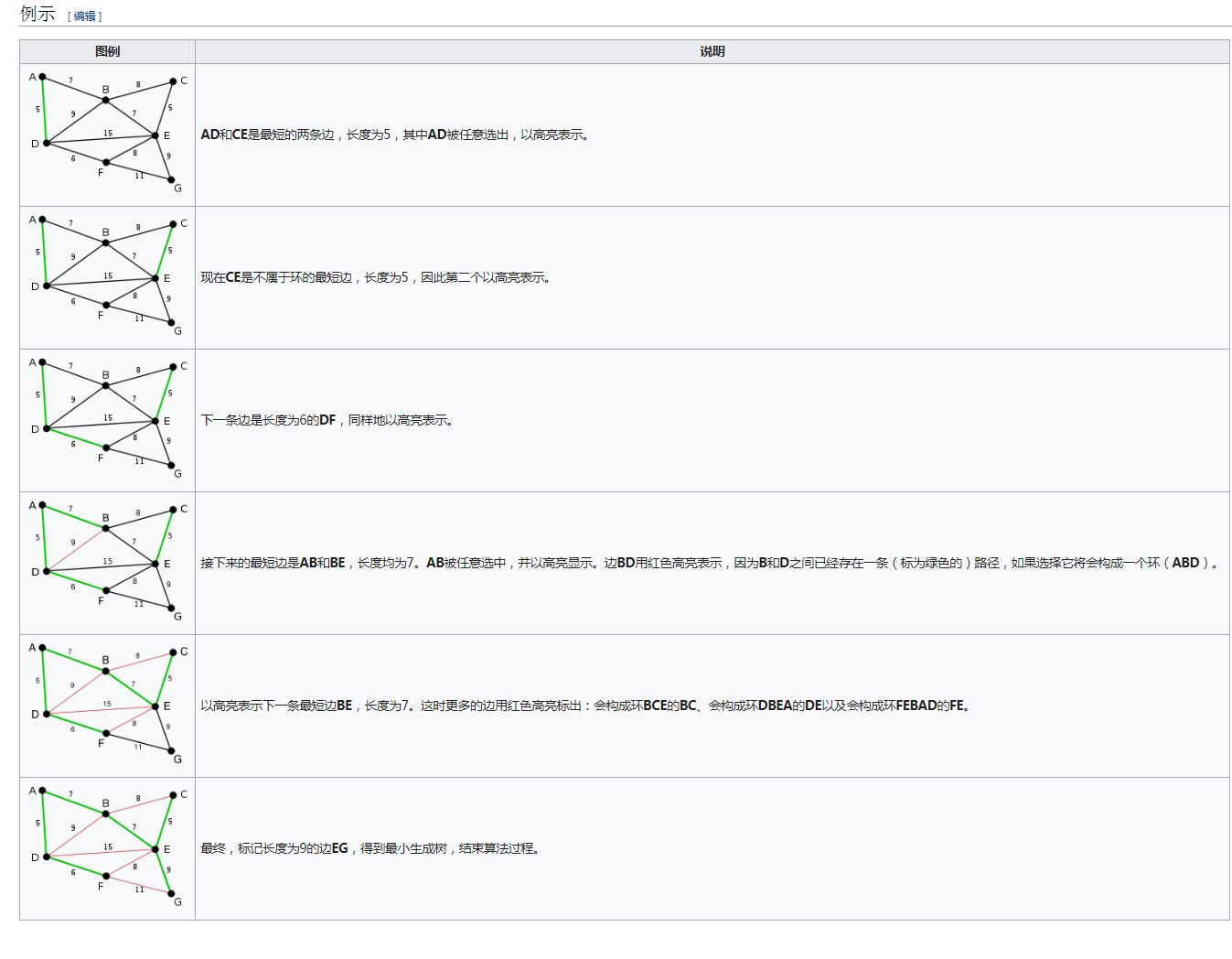
就是先找出一个图的所有的边 按照权重从小到大排序 一次选取权重最小的边 添加到结果图中 注意会跟已经选到的边构成环的边不要选择 抛弃就可以 知道图中的所有节点都在一个连通分量中

上面两种图的算法

其实上面我们要搞清楚
寻找最小生成树的算法

克鲁斯卡尔算法是寻找整个图的边权重之和最小的一种方法 寻找最小生成树

但是上面的两种算法 1.戴克斯克拉算法 2.距离向量算法 这两个算法都是路由选路算法

路由选路算法最终找到的结果并不是最小生成树 而是一个点到其它点距离最小的路径集合 注意这个不一定是最小生成树的