黑白棋论文笔记

机器学习

---

1.引言

状态$S$下，采取最佳行动：

$$A(S) = arg \max_a V(S')$$

$A$: Action

$S'$为$S$执行行动$a$达到的状态

$V(S)$：对状态$S$的评估

主要有两种方法：

1. 搜索，搜索终止状态调用评估函数
2. 机器学习方法学习一个较好的评估函数

所以问题的重点就是这个评估函数$V(S)$

2. 博弈树搜索

极小极大搜索(MinMaxSearch)

2.1 评估函数

Value:

$$V(S) = \sum_{i=1}^8 \sum_{j=1}^8 w[i, j] * s[i, j] + Mobility(my\_color)$$

其中：

$$s[i, j]=\left\{ \begin{array}{ll} 1 &\text{$color[i, j] = my\_color$},\\ -1 &\text{$color[i, j] = opp\_color$},\\ 0 &\text{else}. \end{array}\right.$$

$w[i, j]$ 为w处的权值，经验数据？？？经验数据？？？

Mobility($my\_color$) 己方行动力大小：定义为可以着子的位置总数

2.2 极大极小搜索

考虑两个人下棋$Black$和$White$：

从$Black$角度来看，每一步总是使自己获得最大收益，我们称之为$Max$过程

从$White$角度来看，每一步要使得自己获得最大收益也就是使$Black$获得最小收益，我们称之为$Min$过程

在不考虑一方停止的情况下，下棋就是$Min$和$Max$相互交替的过程

假设搜索的$depth = 1$,那么$Black$显然会选择令自己收益最大的状态$S'$, 则最大收益为$V(S') - V(S)$, 简称：贪心

假设搜索的$depth = 2$, 那么在$Black$做出一个move之后，$White$显然会选择令$Black$收益最小的状态$S''$, 那么$Black$先生的最大收益就是$V(S'') - V(S)$,

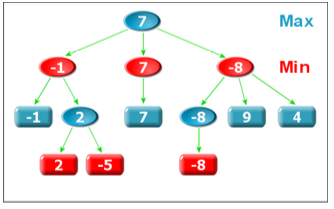
以此类推，$depth$越深，选择会越来越明智.

MinMax dfs

Input: 棋盘$board$, 搜索深度$depth$
Output: 最佳动作$best\_move$

best_val = -INF;
foreach move do
    MakeMove(board, move, my_color); //自己做该move
    val = Min(board, depth - 1);     //对方找一个Min
    UnMakeMove(board, move, my_color);
    if val > best_val:   // 我们需要最大化这个Min
        best_val = val;
        best_move = move;
return best_move

Min

Input: 棋盘$board$, 搜索深度$depth$
Output: 子节点最小值

ans = INF
if (depth < 0) return Value(board);   // Value为估价函数
if (!CanMove(board, opp_color)):
    if (!CanMove(board, my_color)):
        return Value(board);         // Game Over
    return Max(board, depth);        // 白棋停一回合，黑棋走
// 白子可以move
foreach move do:
    MakeMove(board, move, opp_color); // 白棋做一个move
    val = Max(board, depth - 1);      // 黑棋找一个Max
    UnMakeMove(board, move, opp_color);
    ans = min(ans, val); // 白棋需要最小化这个最大值 from Black
return ans;

Max

Input: 棋盘$board$, 搜索深度$depth$
Output: 子节点最大值

ans = -INF
if (depth < 0) return Value(board);  // Value为估价函数
if (!CanMove(board, opp_color)):
    if (!CanMove(board, my_color)):
        return Value(board);         // Game Over
    return Min(board, depth);        //黑棋停一回合，白棋走 
// 黑子可以move
foreach move do:
    MakeMove(board, move, opp_color); // 黑棋做一个move
    val = Min(board, depth - 1);      // 白棋找一个Min
    UnMakeMove(board, move, opp_color);
    ans = max(ans, val); // 白棋需要最小化这个最大值 from Black
return ans;

这个搜算算法逻辑很简单易懂，不过，为了编写代码的方便Min和Max的过程可以合并

如下NegaMax：

Input：棋盘 board, 移动的一方color，搜索深度depth
Output：子节点的最大值

ans = -INF
sign[my_color] = 1;
sign[opp_color] = -1;
if (depth <= 0) return sign[color] * Value(board);
if (!canMove(board, color)):
    if (!canMove(board, color^1)):
        return sign[color] * Value(board);
    return - NegaMax(board, color^1, depth);
foreach move do:
    MakeMove(board, move, color);
    val = -NegaMax(board, color^1, depth-1);
    UnMakeMove(board, move, color);
    ans = max(ans, val);
return ans;

Alpha-Beta 搜索

先看个栗子🌰

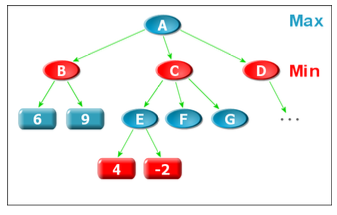
A是Max节点，取B、C、D的最大值，dfs(A)，我们首先会调用Min(B), 得到B的值为6，随后Min(C)，在这过程中我们先Max(E) = 4, 到现在我们可以发现：因为C是Min节点，所以，M(C) <= 4, 而因为A是Max节点，搜索过B之后我们得到的结论是Max(A) >= 6, 至此，我们得到结论：C是个没有用的节点，那么对F和G的搜索也是没有必要的，下一步可以直接搜索D节点...

剪枝，剪枝，剪枝！！！

为了利用这个性质，我们决定引入两个值：$\alpha$ 和 $\beta$， 分别表示节点估值的下界和上界，

AlphaBeta搜索

Input: 棋盘 board, alpha $\alpha$, beta $\beta$(为方便代码中用a和b表示)，移动的一方 color，搜索深度depth
Output: 子节点最大值

ans = -INF;
sign[my_color] = 1;
sign[opp_color] = -1;
if (depth <= 0) return sign[color] * Value(board);
if (!canMove(board, color)):
    if (!canMove(board, color^1)):
        return sign[color] * Value(board);
    return - AlphaBeta(board, -b, -a, color^1, depth);
foreach move do:
    MakeMove(board, move, color);
    val = -AlphaBeta(board, -b, -a, -1, color^1);
    UnmakeMove(board, move, color);
    if (val > a && val >= b) return val;
    a = max(a, val);
return ans;

加入一些其他的优化姿势

AlphaBeta搜索的节点大致可以分为三类（以Max），过程为例：

1. $val <= \alpha$，直接return
2. $val >= \beta$，$\beta$剪枝，更新$\alpha$的值
3. $\alpha < val<\beta$，没有剪枝，继续搜索

我们可以估算价值然后进行排序来改变搜索顺序，使得剪枝的节点尽量多

and，一个棋盘状态$board$可以在双方不同的走法中走到，但是这个$board$实际上只需要搜索一次，我们可以记录他的值，下一次访问到的时候直接return，其实是一个记忆化的过程