搜索和图论入门

NOIP

dfs练习，数独

POJ3676

Description

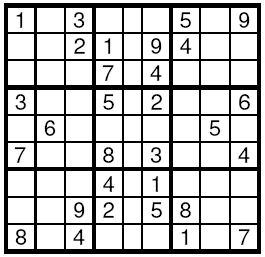
Sudoku is a very simple task. A square table with 9 rows and 9 columns is divided to 9 smaller squares 3x3 as shown on the Figure. In some of the cells are written decimal digits from 1 to 9. The other cells are empty. The goal is to fill the empty cells with decimal digits from 1 to 9, one digit per cell, in such way that in each row, in each column and in each marked 3x3 subsquare, all the digits from 1 to 9 to appear. Write a program to solve a given Sudoku-task.

Input

The input data will start with the number of the test cases. For each test case, 9 lines follow, corresponding to the rows of the table. On each line a string of exactly 9 decimal digits is given, corresponding to the cells in this line. If a cell is empty it is represented by 0.
Output

For each test case your program should print the solution in the same format as the input data. The empty cells have to be filled according to the rules. If solutions is not unique, then the program may print any one of them.
Sample Input

1
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107

Sample Output

143628579
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127

bfs练习

神秘的别墅

3 ． 神秘的别墅
（villa.pas/c/cpp ）
【问题描述】
布莱克先生是土尔其总统的顾问，因此他也将前往参加北约峰会。他喜欢单独居住，
远离商业中心的宾馆。于是他在奥瑞契佛加租了一间大的别墅。但有一件事搅扰了他：
尽管大多数的房间都有电灯开关，但这些开关经常只能控制其它房间的灯而不是自己房
间的。但是房产经纪人却认为这是一个特色，布莱克先生只能认为当电工们将开关连接
到框架上时，他们是心不在焉的。
有些夜晚，布莱克先生回来的很晚，当他站在门厅中时，所有其它房间的灯都是关
的。因为布莱克先生怕黑，所以他不敢进入黑暗的房间，也不敢关掉他所在房间的灯。
布莱克先生想利用这些接错位置的开关帮助他前进。他希望能走到卧室并关掉卧室以外
所有的灯。
编写程序，根据给定的房间说明，考虑当仅有门厅中亮的时候，你如何从门厅到卧
室。不可以进入一个黑暗的房间，只能在房间中关自己房间的开关，最后时，除了卧室
以外的灯其余的灯都必须关闭，每个房间都只有一盏灯。如果有几种办法可以通往卧室，
你必须找出使用步数最少的方法。其中“从一个房间到另一个房间”，“开灯”和“关灯”
每个过程算一步。
【输入文件】
输入文件 villa.in 中：
输入文件第一行包含三个整数 R，D 和 S。R 表示别墅的房间数，1<=R<=10,D 表示房
间之间连接的门数，S 表示别墅中灯的开关数。房间用数字 1 到 R 标识，1 号房间表示门
厅，R 房间表示卧室。接下来的 D 行每行包含两个整数 I 和 J，表示房间 I 和房间 J 之间
有一扇门连接。接下来的 S 行每行包含两个整数 K 和 L，表示房间 K 中有一个开关控制房
间 L 中的电灯。
【输出文件】
输出文件 villa.out 中：
输出一行解。如果对于布莱克先生有解，则输出“Mr.Black needs X Steps.”其中
X 表示来到他的卧室并将所有其它房间的灯关掉所需的最少步数。如果无解，输出“Poor
Mr. Black! No sleep tonight!”
【输入样例 1】
3 3 4
1 2
1 3
3 2
1 2
1 3
2 1
3 2
【输出样例 1】
Mr. Black needs 6 steps.

图论通用模板

闭眼可敲，改编自刘汝佳的图论板，不过改用了前向星建图，防止卡常
本册大部分图论算法都基于本模板

struct graph{
    struct Edge{
        int from, to, cost, nxt;
        Edge(){}
        Edge(int x, int y, int z, int w):from(x), to(y), cost(z), nxt(w){}
    } edges[M];
    int n, head[N], E;
    inline void init(int _n){
        n = _n; E = 0;
        for (int i = 0; i <= n; i++) head[i] = -1;
    }
    inline void addEdge(int f, int t, int c){
        edges[E] = Edge(f, t, c, head[f]);
        head[f] = E++;
    }
} g;

最短路 SPFA

bool inq[N];
int dist[N];
inline int spfa(const int &s, const int &t){
    queue <int> Q;
    memset(inq, 0, sizeof(inq));
    memset(dist, INF, sizeof(dist));
    dist[s]=0; inq[s]=1;
    for (Q.push(s); !Q.empty();){
        int u = Q.front(); Q.pop(); inq[u]= 0;
        for (int i = head[u]; ~i; i = edges[i].nxt){
            Edge &e = edges[i];
            if (dist[u] + e.cost < dist[e.to]){
                dist[e.to] = dist[u] + e.cost;
                if (!inq[e.to]){
                    Q.push(e.to);
                    inq[e.to] = 1;
                }
            }
        }
    }
    return dist[t];
}

对了，多元最短路floyed，这里就不多说了

匈牙利
点这里
二分图匹配（匈牙利算法的DFS实现）
INIT：g[][]两边定点划分的情况
CALL:res=hungary();输出最大匹配数
优点：适于稠密图，DFS找增广路快，实现简洁易于理解
时间复杂度:O(VE);

#include<bits/stdc++.h>
using namespace std;
const int N = 200 + 7;
const int INF = 0x3f3f3f3f;
struct Hungary{
    vector <int> G[N];
    bool used[N];// main里面记得memset
    int girl[N], n;
    inline void init(int _n){
        n = _n;
        for (int i = 0; i <= n; i++) G[i].clear();
    }
    inline void addEdge(const int &u, const int &v){
        G[u].push_back(v);
        //printf("addEdge %d %d\n", u, v);
    }
    bool Find(int x){
        for (int i = 0; i < G[x].size(); i++){    //扫描每个妹子
            int j = G[x][i];
            if (used[j]) continue;
            // 如果有暧昧并且还没有标记过
            // (这里标记的意思是这次查找曾试图改变过该妹子的归属问题，
            // 是没有成功，所以就不用瞎费工夫了）
            used[j] = 1;
            if (girl[j] == -1 || Find(girl[j])) {
                //名花无主或者能腾出个位置来，这里使用递归
                girl[j] = x;
                return true;
            }
        }
        return false;
    }
    inline int hungary(const int &n, const int &m){
        int all = 0;
        memset(girl, -1, sizeof girl);
        for (int i = 0; i < n; i++) {
            memset(used, 0, sizeof(used)); //这个在每一步中清空
            if (Find(i)) all += 1;
        }
        //for (int i = 0; i < m; i++) printf("girl[%d] = %d\n", i, girl[i]);
        //printf("all = %d\n", all);
        return all;
    }
} hg;