机器学习

Assignment3: 数据中心化

陈伟文 10152510217

2017/10/15

关于中心化

以PCA为例说下中心化的作用。
下面两幅图是数据做中心化（centering）前后的对比，可以看到其实就是一个平移的过程，平移后所有数据的中心是（0，0）.

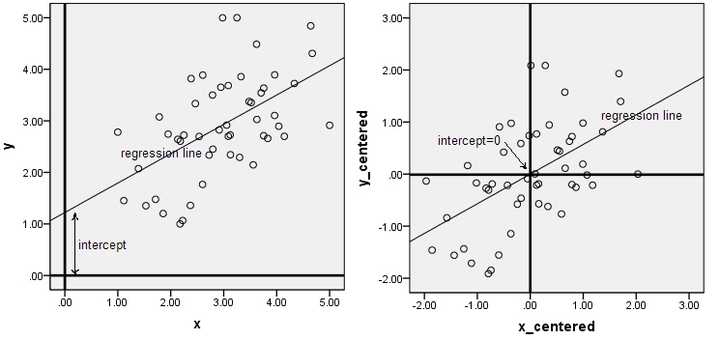
在做PCA的时候，我们需要找出矩阵的特征向量，也就是主成分（PC）。比如说找到的第一个特征向量是a = [1, 2]，a在坐标平面上就是从原点出发到点（1，2）的一个向量。如果没有对数据做中心化，那算出来的第一主成分的方向可能就不是一个可以“描述”（或者说“概括”）数据的方向了。还是看图比较清楚。

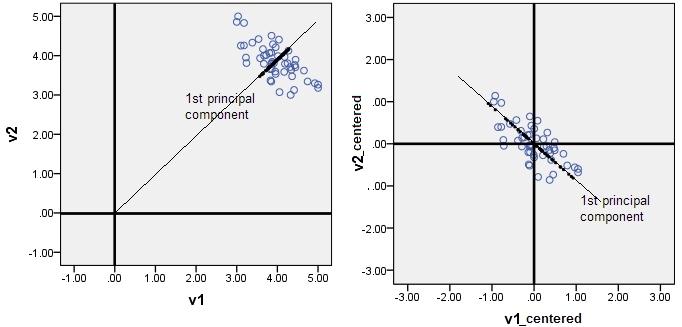
黑色线就是第一主成分的方向。只有中心化数据之后，计算得到的方向才能比较好的“概括”原来的数据。黑色线就是第一主成分的方向。只有中心化数据之后，计算得到的方向才能比较好的“概括”原来的数据。

回头看题目

在对高维数据降维前应先进行“中心化”，常见方法是将协方差矩阵$XX^T$转换为$XHH^TX^T$，其中$H = I - \frac 1 m 11^T，分析其效果$

主要分析H，中心化的作用就是减掉平均值$\mu$，
把H带入原式，则$XH = XI - \frac 1 m X 11^T$
期中$I$为单位矩阵，所以$XI = I$,
若数据$X =$为$k*m$矩阵，即$n$个数据$k$维，

$X = \begin{bmatrix} x_{11} & x_{12} & ... & x_{1n}\\ x_{21} & x_{22} & ... & x_{2n}\\ ... & ... & ... & ...\\ x_{k1} & x_{k2} & ... & x_{kn}\\ \end{bmatrix}$式子中的$1 = \begin{bmatrix} 1\\ 1\\ ...\\ 1\end{bmatrix}$:一个 $n * 1$ 的单位列向量，

则$\frac 1 m X1 = \frac 1 m \begin{bmatrix} \sum_{i=1} ^ n x_{1i}\\ \sum_{i=1} ^ n x_{2i}\\ ...\\ \sum_{i=1} ^ n x_{ni} \end{bmatrix}$即每一维度对应的均值$\mu$

记$\mu_j = \frac 1 m \sum_{i=1} ^ n x_{1i}$为第$j$个维度的均值

继续算下去，$\frac 1 m X 11^T =\begin{bmatrix} \ \mu_1 & \mu_1 & ... & \mu_1\\ \ \mu_2 & \mu_2 & ... & \mu_2\\ \ ... & ... & ... & ...\\ \ \mu_k & \mu_k & ... & \mu_k \\ \end{bmatrix}$，一个$k*n$的矩阵，每行为该维的均值

现在可以看出这个结果了：

$XH = XI - \frac 1 m X 11^T = \begin{bmatrix} \ x_{11} - \mu_1 & x_{12} - \mu_1 & ... & x_{1n} - \mu_1\\ \ x_{21} - \mu_2 & x_{22} - \mu_2 & ... & x_{2n} - \mu_2\\ \ ... & ... & ... & ...\\ \ x_{k1} - \mu_k & x_{k2} - \mu_k & ... & x_{kn} - \mu_k\\ \end{bmatrix}$，

实现了$x' = x - \mu$的效果，使得新的均值为$0$

至于$H^TX^T$同理吧，不过，这个协方差矩阵为啥长这样还有些疑惑(可能是因为上课神游了)

老师下次讲题目的时候能不能提一下协方差矩阵啊

参考文献

彭先生的blog

知乎:数据中心化与标准化