Enzyme Kinetic Simulation

Enzyme_Kinetics iGEM Modelling

---

---

Introduction

Our project this year concentrates mainly on the metabolic circuit of cordycepin (COR) and pentostatin (PTN). It involves three enzymes, cns1, cns2 and cns3-HisG domain. Since all our work is related to these three enzymes, it is necessary to depict the overall picture of the enzymatic system.

Generally, our aim of constructing the enzyme kinetic simulation is divided into two parts. Firstly, we would like to theoretically give the model that testifies the necessity of using fusion expression of cns1 and cns2 in experiments, which can give powerful support and confidence to the later experiments of fusion expression. Additionally, we would like to discover how the diffusion rate influences the production rate. Secondly, since our goal is to co-ferment cordycepin and pentostatin furthest, we have to build a model that consists of all the elements involved in the metabolic circuit of cordycepin and pentostatin. More importantly, we need to find the correlation between the concentration of cordycepin and pentostatin, as well as give the optimal substitute ratio and optimal expression strength of the enzymes.

1 Fusion-Expression Simulation

Our task is to deal with the circuit below. In the circuit, cns2 converts 3'-AMP to the enol state of 2'-C-3'-dA, which then naturally converts to the keto state. Enzyme cns3 produces cordycepin using the product from cns2.

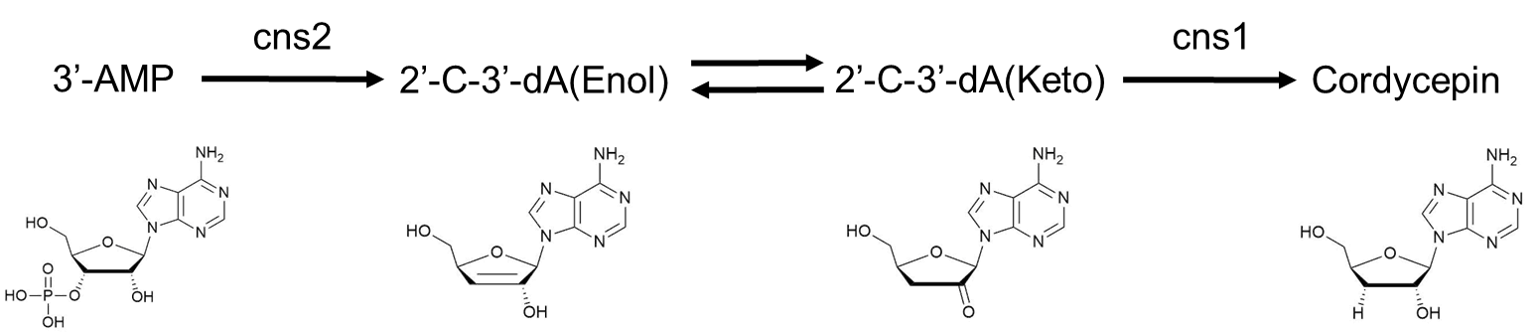
This modeling section aims to compare the efficiency of the enzymatic reactions using a fusion-expression strategy to that using a separate-expression strategy, which in result will give theoretical support for the corresponding experiments.

It is reported in literature that there exists interaction between cns1 and cns2 in vivo by yeast two-hybrid analysis [Xia Y et al. (2017)]. The phenomenon of interaction between two or more enzymes is not peculiar. It is common to see some multienzyme complex in nature, including pyruvate dehydrogenase, rubisco and even respiratory electron-transport chain, which is recently proven to be a megacomplex. The common consensus about the multienzyme complex is that it allows to segregate certain biochemical pathways into one place in the cell, which increases the catalytic efficiency and reduces side effects. In nature, the expression of enzymes in the multienzyme complex is generally independent, after which they meet and combine into a multienzyme complex.

In the theory of structural biology, the fusion-expression strategy connects the two enzymes during expression so that the substitute of the first enzyme is sequentially converted to the product of the second enzyme, which is more efficient than separate-expression strategy. However, it has not been mathematically proven in enzyme kinetics. Additionally, the evaluation of the linker connecting the enzymes is obscure before doing specific enzyme-activity experiments.

Here, we would like to build an enzyme kinetic model to simulate the separate-expression strategy and the fusion-expression strategy. Determination of the linker is conducted in computational structural biology model.

It is reported that keto-enol tautomerism can be simulated as a first-order reaction [Huang L et al. (2007)] and can be represented as:

$$\frac{dC}{dt} = -k_{eq}C$$

in which $C$ is the concentration of the keto form.

• General Assumption: Our enzyme kinetic simulation is assumesdin vivo, so all the enzymatic reaction is reversable and 2'-C-3'-dA is considered to be all in keto form ($k_{eq} = \frac{[Enol form]}{[Keto form]} \ll 1$).

1.1 Distance between molecules in solution

The difference between these two strategies is the relative concentration of the substitute of the second enzyme, since the concentration is lower in seperate-expression strategy because the product of the first enzyme (which is at the same time the substitute of the second enzyme) need to diffuse to the second enzyme.

Considering cns1 and cns2 enzyme diffusing in the solvent, the initial concentration of the enzymes is uniform in the whole system. When the substitute of the first enzyme is converted into the product, it needs to diffuse to the second enzyme.

Therefore, the diffusing distance is the key issue in our simulation of separate expression.

Firstly, we shoule consider the distance

• Assumption 1: Reaction environment can be treated as solution and the solution is uniform, which means that the concentration of the solvent at one position is the same with that at any other positions in the solution.
• Assumption 2: All the enyzmes can be assumed as spheres.

The average distance between molecules in a solution and the average radius of a molecule is calculated by Kozanecki et al. [Kozanecki M et al. (2016)]

It is frequently useful to know the average volume of solution occupied by each molecule, or more directly, the average distance separating molecules in solution. This is a simple calculation based only on the molar concentration. In a 1 M solution, there are $6×10^{23}$ molecules/L, = 0.6 molecules/$\text{nm}^3$, or inverting, the volume per molecule is V=1.66 $nm^3$/molecule at 1 M. For a concentration C, the volume per molecule is V=1.66/C. So, the distance between molecule in average is:

$$d = V^{\frac{1}{3}} = 1.18/C^{\frac{1}{3}}$$

What we really want is a physically intuitive parameter for the
size of the protein. If we assume the protein has the simplest
shape, a sphere, we can calculate its radius. We will refer to this
as $R_\text{min}$, because it is the minimal radius of a sphere that could contain the given mass of protein:

$$R_\text{min} = (3V/4\pi)^{\frac{1}{3}} = 0.066M^{\frac{1}{3}} (\text{for M in Dalton}, R_{min} \text{in nanometer})$$

Since the concentration of the enzyme in the cell is in the $\mu \text{mol}$ magnitude, the distance between protein molecules is in the hundred-nanometer magnitude. In our project, the mass of cns1, cns2, cns3 is around 80, 40, 100 kD respectively, so the radius of the enzyme is around 3 nm, which is in the unit-nanometer magnitude. Compared to the distance between enzymes, the radius is negligible.

• Assumption 3: In the simulation of the fusion-expression, the enzyme is treated as a point, rather than a sphere.

To calculate the distance between cns1 and cns2 in the mixed solution of the system, we make another assumption to simplify the model.

• Assumption 4: The two enzymes are evenly distributed in the whole solution.

Thus, if we assume the concentration of cns1 to be $C_\text{cns1}$, and concentration of cns2 to be $C_\text{cns2}$, there are totally $(C_\text{cns1}+C_\text{cns2})\times 6.02\times 10^{23}$ molecules in 1 L system. As the calculation above, the distance between two enzymes can be represented by:

$$d_{cns1,cns2} = 1.18/(C_{cns1}+C_{cns2})^{\frac{1}{3}}$$

Compared to the separate-expression strategy, the fusion-expression strategy enables relatively no distance between cns1 and cns2, as they are connected using the linker.

1.2 Diffuson Simulation

During the diffusion process, the concentration of the substitute of the second enzyme is related to the product of the first enzyme by the diffusion model. Since all the molecule are evenly distributed, the three-dimentional system can be simplified to one-dimentional system because we only need to consider the relation between one cns2 enzyme and the nearest cns1 enzyme.

Here, we use Fick's law to describe the diffusion process. (https://en.wikipedia.org/wiki/Fick%27s_laws_of_diffusion)

• Assumption 5: A concentration gradient is the only force driving substrate motion in the system, ignoring the influence of charge interactions or the shape of the molecule. [Eun C et al. (2014)]

According to Fick's first law of diffusion, [Rice S et al. (1985)]

$$J(z,t) = -D \frac{\partial c(z,t)}{\partial z}$$

• $J$ is the diffusion flux, of which the dimension is amount of substance per unit area per unit time. $J$ measures the amount of substance that will flow through a unit area during a unit time interval.
• $D$ is the diffusion coefficient or diffusivity. Its dimension is area per unit time.
• $c$ is the concentration, of which the dimension is amount of substance per unit volume.
• $z$ is position, the dimension of which is length.

In the equation, the minus sign indicates that the flow occurs from the concentrated to the dilute region of the solution. [Macheras P et al. (2006)]

If we treat the situation in a discretized way, the Fick's first law of diffusion can be interpreted in:

$$J(z,t) = -D \frac{\Delta c(z,t)}{\Delta z} =-D\frac{c(z+1,t)-c(z,t)}{(z+1)-z}$$

Therefore, the flux of a position is related to the concentration gradient of this position.

When we consider the change of the concentration as the fuction of the time, we can get:

$$\frac{\partial c(z,t)}{\partial t} = - \frac{\partial}{\partial x} J = \frac{\partial}{\partial x}(D\frac{\partial}{\partial x} c(z,t)) = D\frac{\partial ^2 c(z,t)}{\partial x^2}$$

This formula is called Fick's second law of diffusion. Given the initial condition that $c(0,0) = c_l(t)$ and $c(\delta,0) = c_r(t)$, the differential ordinary equation can be solved as the form below. [M.H. Jacobs. (1935)]

$$c(z,t) = c_l(t)+[c_r(t)-c_l(t)]\frac{z}{\delta}+\frac{2}{\pi}\sum_{i=1}^{\infty}{\frac{c_r(t)cosi\pi -c_l(t)}{i}}sin(i\pi \frac{z}{\delta})exp(-\frac{D}{\delta^2}i^2\pi^2 t)$$

In this equation, $c_r(t)$ is the substitute concentration of the second enzyme around the second enzyme, while $c_l(t)$ is the substitute concentration of the second enzyme in the context of the first enzyme. These two concentrations are independent to the diffusion process, but dependent on the production and consumption of substance.

If we fix $z$ to $\delta$, we can get:

$$c(z=\delta,t) = c_r(t)+\frac{2}{\pi}\sum_{i=1}^{\infty}{\frac{c_r(t)cosi\pi -c_l(t)}{i}}sin(i\pi )exp(-\frac{D}{\delta^2}i^2\pi^2 t)$$

Since $sin(i\pi) = 0$,

$$c(z=\delta,t) = c_r(t)$$

In this case, this equation is meaningless at the position of the second enzyme, but if we consider the position near the second enzyme, which makes the $sin(i\pi) \neq 0$ but very small. Based on this manipulation, the equation above is meaningful. Since the equation is too complicated to fit in our case, we'd like to simplify it to this form.

$$c(z=\delta,t) = c_r(t) - k_\text{diff}\frac{c_r(t)-c_l(t)}{exp(\delta)}$$

Since $\delta$ is the distance between the source and the point of interest, if we do not fix $\delta$, but set it to a parameter $x$, we can get:

$$c(x,t) = c_r(t) - k_\text{diff}\frac{c_r(t)-c_l(t)}{exp(x)}$$

Because $c_r(t)$ and $c_l(t)$ is independent to the diffusion process, they can be represented to $c_r$ and $c_l$, which is consistent to the equations in enzyme kinetics. $c(x,t)$ is the updated concentration of the substance near the second enzyme which is affected by diffusion. So the equation looks like:

$$\frac{dc_r}{dt} = k_\text{diff}\frac{c_l-c_r}{exp(x)}$$

This equation describes that the derivation of the concentration in the low concentration area is proportional to the difference between the concentrations and nonlinearly inversely proportional to the distance $x$. The coefficient $k_\text{diff}$ represents the diffusion rate of stubstances in the solution. Since we have no access to the value of this parameter, we set it to an optional value and investigate the influence on the model by this value.

1.3 Enzyme Kinetics Simulation of Fusion Expression

1.3.1 Fusion Expression Simulation with limited resource

Fusion-expression strategy enables the enzyme cns1 and cns2 to be expression linkly and closely in distance. The product of the first enzyme instantaneously functions as the substitute of the second enzyme and is converted to the end product, cordycepin.

Based on all the assumption and prerequisite derivation. we can create the follow diagram based on typical enzyme kinetics:

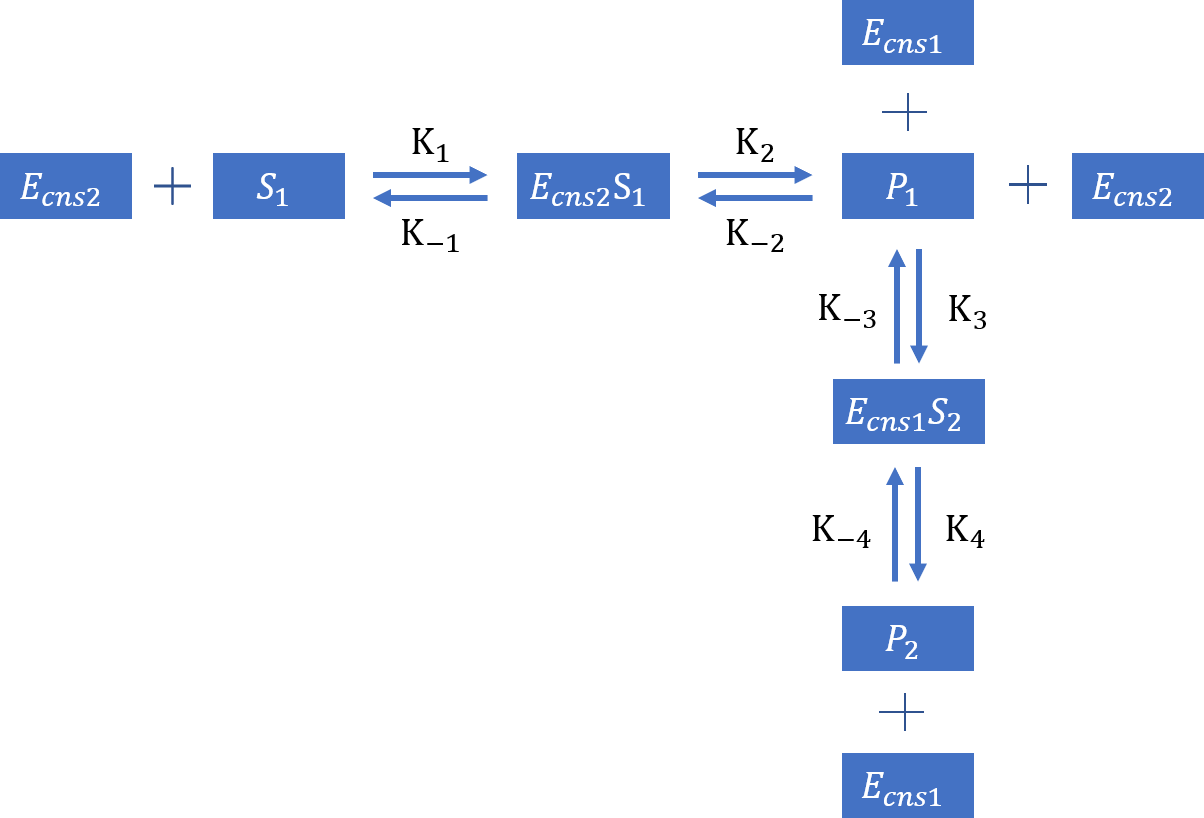
Based on mass action law, we can now list the equations:

$$\frac{d[S_1]}{dt} = -k_1[E_\text{cns2}][S_1] + k_{-1}[E_\text{cns2}S_1]$$

$$\frac{d[E_\text{cns2}]}{dt} = -k_1[E_\text{cns2}][S_1] + k_{-1}[E_\text{cns2}S_1] + k_2[E_\text{cns2}S_1] - k_{-2}[P_{1}][E_\text{cns2}]$$

$$\frac{d[E_\text{cns2}S_1]}{dt} = k_1[E_\text{cns2}][S_1] - k_{-1}[E_\text{cns2}S_1] - k_2[E_\text{cns2}S_1] + k_{-2}[P_{1}][E_\text{cns2}]$$

$$\frac{d[P_1]}{dt} = k_2[E_\text{cns2}S1]-k_{-2}[P_1][E_\text{cns2}]-k_3[E_\text{cns1}][P_1]+k_{-3}[E_\text{cns1}S_2]$$

$$\frac{d[E_\text{cns1}]}{dt} = -k_{3}[E_\text{cns1}][P_{1}] + k_{-3}[E_{cns1}S_2] + k_4[E_{cns1}S_2] - k_{-4}[P_2][E_{cns1}]$$

$$\frac{d[E_\text{cns1}S_2]}{dt} = k_3[E_\text{cns1}][P_{1}] - k_{-3}[E_\text{cns1}S_2] - k_4[E_\text{cns1}S_2] + k_{-4}[P_2][E_\text{cns1}]$$

$$\frac{d[P_2]}{dt} = k_4[E_\text{cns1}S_2] - k_{-4}[P_2][E_\text{cns1}]$$

Based on the derivation of Michaelis-Menten equation, from the equation of $\frac{d[E_\text{cns2}]}{dt}$ and $\frac{d[E_\text{cns2}S_1]}{dt}$, we can find that $\frac{d[E_\text{cns2}]}{dt}+\frac{d[E_\text{cns2}S_1]}{dt} = 0$, which means that the value of $[E_\text{cns2}]+[E_\text{cns2}S_1]$ is a constant. Here, we defind this constant as $E_\text{ini2}$, which represents the constant of the initial concentration of cns2 enzyme. Likewise, considering to cns1 enzyme, value of $[E_\text{cns1}]+[E_\text{cns1}S_2]$ is a constant, which is defined as $E_\text{ini1}$.

Therefore, the equations convert to:

$$\frac{d[S_1]}{dt} = -k_1[E_\text{cns2}][S_1] + k_{-1}(E_\text{ini2}-[E_\text{cns2}])$$

$$\frac{d[E_\text{cns2}]}{dt} = -k_1[E_\text{cns2}][S_1] + (k_{-1}+k_2)(E_\text{ini2}-[E_\text{cns2}]) - k_{-2}[P_{1}][E_\text{cns2}]$$

$$\frac{d[P_1]}{dt} = k_2(E_\text{ini2}-[E_\text{cns2}])-k_{-2}[P_1][E_\text{cns2}]-k_3[E_\text{cns1}][P_1]+k_{-3}(E_\text{ini1}-[E_\text{cns1}])$$

$$\frac{d[E_\text{cns1}]}{dt} = -k_{3}[E_\text{cns1}][P_{1}] + (k_{-3}+k_4)(E_\text{ini1}-[E_\text{cns1}]) - k_{-4}[P_2][E_\text{cns1}]$$

$$\frac{d[P_2]}{dt} = k_4(E_\text{ini1}-[E_\text{cns1}]) - k_{-4}[P_2][E_\text{cns1}]$$

MATLAB Code:

function [f] = dXdT(t, x)
k1F = 1;
k1R = 0.1;
k2F = 2;
k2R = 0.1;
k3F = 1;
k3R = 0.1;
k4F = 1;
k4R = 0.1;
E01 = 1;
E02 = 1;
s1=x(1);
e1=x(2);
p1=x(3);
e2=x(4);
p2=x(5);
%ds1dt = 0;
ds1dt = -k1F*e1*s1 + k1R*(E01-e1);
de1dt = -k1F*e1*s1 + (k1R+k2F)*(E01-e1) - k2R*p1*e1;
dp1dt = k2F*(E01-e1) - k2R*p1*e1 - k3F*e2*p1 + k3R*(E02-e2);
de2dt = -k3F*e2*p1 + (k3R+k4F)*(E02-e2) - k4R*p2*e2;
dp2dt = k4F*(E02-e2) - k4R*p2*e2;
f = [ds1dt; de1dt; dp1dt; de2dt; dp2dt];
end
tspan = 0:0.001:10;
initial = [1,1,0,1,0];
[t,x] = ode45( @dXdT, tspan, initial);

Solving the ordinary differential equation system will give us the concentration deviation of the substitute, intermediate product and end product, which is 3'-AMP, 2'-C'-3'-dA and cordycepin respectively. In this simulation, the resource is limited, which means that the substitutes will deplete without any supplement.

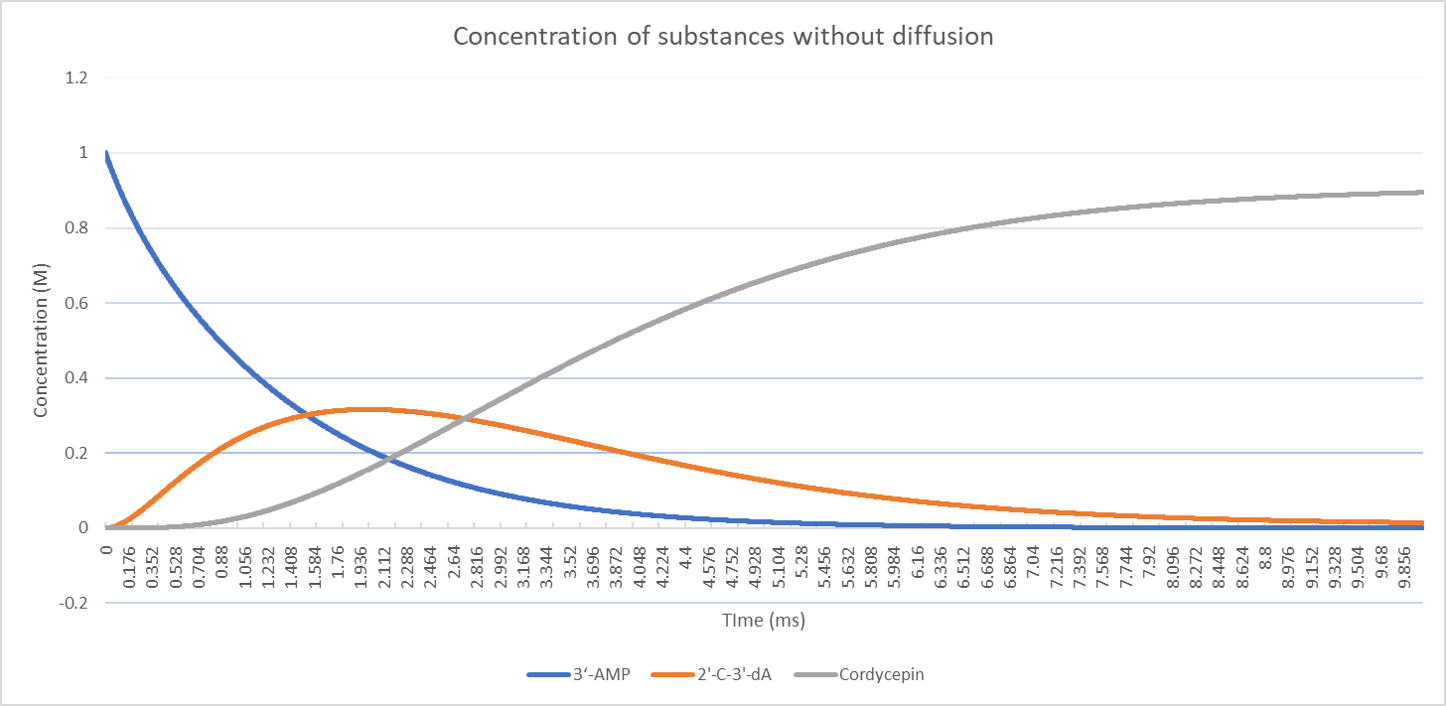
In the figure, the final concentration of the end product, cordycepin, under this set of parameters, is around 0.89. The value of the cordycepin concentration is meaningless, since all the parameters are set optionally. However, it provides a model which can be used in comparison of the separate-expression strategy with the same set of parameters.

1.3.2 Fusion Expression Simulation with abundant resource

The substitute of cns2 is 3'-AMP, while the substitue of cns3-HisG domain is adenosine, which both are the basic substances and liable to produce in a cell. If we provide abundant resource, the concentration of the substitutess are considered to be constant.

Therefore, we need to alter the equations of the substitute concentration. We fix the concentration of $S_1$ (3'AMP) to be constant, and let other equations unchanged.

$$\frac{d[S_1]}{dt} = 0$$

The result is below:

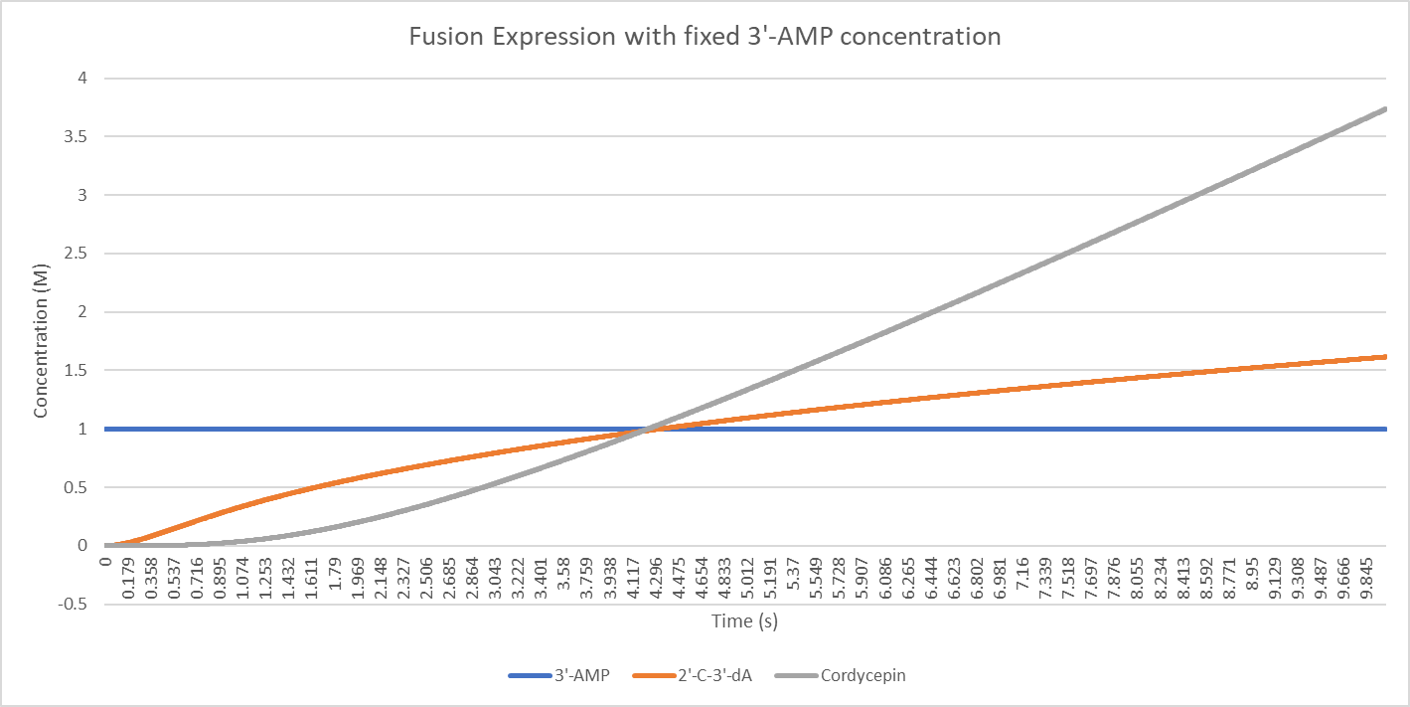
From the figure above, we can see that the concentration of the intermediate product 2'-C-3'-dA rises slowly while the end product cordycepin rises much more quickly.

1.4 Enzyme Kinetics Simulation of Separate Expression with Diffusion

Considering the separate-expression strategy, we add the diffusion process into the diagram and we can create the following diagram:

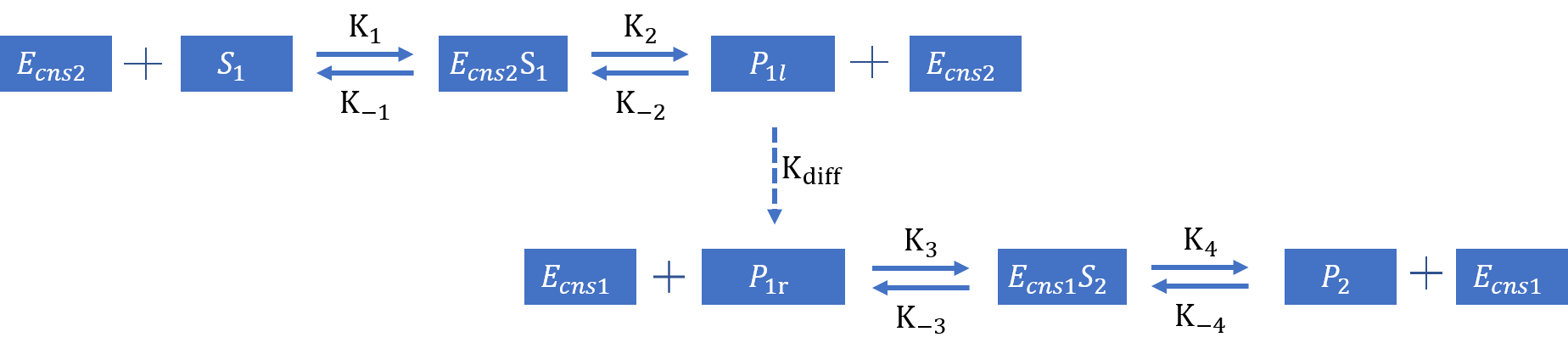
1.4.1 Separate Expression Simulation with limited resource

Adding the term of the diffusion process, we can now list the ordinary differential equations:

$$\frac{d[S_1]}{dt} = -k_1[E_\text{cns2}][S_1] + k_{-1}[E_\text{cns2}S_1]$$

$$\frac{d[E_\text{cns2}]}{dt} = -k_1[E_\text{cns2}][S_1] + k_{-1}[E_\text{cns2}S_1] + k_2[E_\text{cns2}S_1] - k_{-2}[P_{1l}][E_\text{cns2}]$$

$$\frac{d[E_\text{cns2}S_1]}{dt} = k_1[E_\text{cns2}][S_1] + - k_{-1}[E_\text{cns2}S_1] - k_2[E_\text{cns2}S_1] + k_{-2}[P_{1l}][E_\text{cns2}]$$

$$\frac{d[P_{1l}]}{dt} = k_2[E_\text{cns2}S_1] - k_{-2}[P_{1l}][E_\text{cns2}] - K_\text{diff}\frac{[P_{1l}]-[P_{1r}]}{exp(d_\text{cns1,cns2})}$$

$$\frac{d[P_{1r}]}{dt} = K_\text{diff}\frac{[P_{1l}]-[P_{1r}]}{exp(d_\text{cns1,cns2})} - k_3[E_\text{cns1}][P_{1r}] + k_{-3}[E_\text{cns1}S_2]$$

$$\frac{d[E_\text{cns1}]}{dt} = -k_{3}[E_\text{cns1}][P_{1r}] + k_{-3}[E_\text{cns1}S_2] + k_4[E_\text{cns1}S_2] - k_{-4}[P_2][E_\text{cns1}]$$

$$\frac{d[E_\text{cns1}S_2]}{dt} = k_3[E_\text{cns1}][P_{1r}] - k_{-3}[E_\text{cns1}S_2] - k_4[E_\text{cns1}S_2] + k_{-4}[P_2][E_\text{cns1}]$$

$$\frac{d[P_2]}{dt} = k_4[E_\text{cns1}S_2] - k_{-4}[p_2][E_\text{cns1}]$$

From the equation of $\frac{d[E_\text{cns2}]}{dt}$ and $\frac{d[E_\text{cns2}S_1]}{dt}$, we can find that $\frac{d[E_\text{cns2}]}{dt}+\frac{d[E_\text{cns2}S_1]}{dt} = 0$, which means that the value of $[E_\text{cns2}]+[E_\text{cns2}S_1]$ is a constant. Here, we defind this constant as $E_{ini2}$, which represents the constant of the initial concentration of cns2 enzyme. Likewise, considering to cns1 enzyme, value of $[E_\text{cns1}]+[E_\text{cns1}S_2]$ is a constant, which is defined as $E_\text{ini1}$.

Therefore, the equations convert to:

$$\frac{d[S_1]}{dt} = -k_1[E_\text{cns2}][S_1] + k_{-1}(E_\text{ini2}-[E_\text{cns2}])$$

$$\frac{d[E_\text{cns2}]}{dt} = -k_1[E_\text{cns2}][S_1] + (k_{-1}+k_2)(E_\text{ini2}-[E_\text{cns2}]) - k_{-2}[P_{1l}][E_\text{cns2}]$$

$$\frac{d[P_{1l}]}{dt} = k_2(E_\text{ini2}-[E_\text{cns2}]) - k_{-2}[P_{1l}][E_\text{cns2}] - k_\text{diff}\frac{[P_{1l}]-[P_{1r}]}{exp(d_\text{cns1,cns2})}$$

$$\frac{d[P_{1r}]}{dt} = k_\text{diff}\frac{[P_{1l}]-[P_{1r}]}{exp(d_\text{cns1,cns2})} - k_3[E_\text{cns1}][P_{1r}] + k_{-3}(E_\text{ini1}-[E_\text{cns1}])$$

$$\frac{d[E_\text{cns1}]}{dt} = -k_{3}[E_\text{cns1}][P_{1r}] + (k_{-3}+k_4)(E_\text{ini1}-[E_\text{cns1}]) - k_{-4}[P_2][E_\text{cns1}]$$

$$\frac{d[P_2]}{dt} = k_4(E_{ini1}-[E_{cns1}]) - k_{-4}[P_2][E_{cns1}]$$

MATLAB Code:

function [f] = dXdT(t, x)
k1F = 1;
k1R = 0.1;
k2F = 2;
k2R = 0.1;
k3F = 1;
k3R = 0.1;
k4F = 1;
k4R = 0.1;
E1 = 1;
E2 = 1;
s1=x(1);
e1=x(2);
pl=x(3);
pr=x(4);
e2=x(5);
p2=x(6);
kdiff = 10;
d = 1.118/((e1+e2)**(1/3));
ds1dt = -k1F*e1*s1 + k1R*(E1-e1);
de1dt = -k1F*e1*s1 + (k1R+k2F)*(E1-e1) - k2R*pl*e1;
dpldt = k2F*(E1-e1) - k2R*pl*e1 - (kdiff)*(pl-pr)/exp(d);
dprdt = (kdiff)*(pl-pr)/exp(d) - k3F*e2*pr + k3R*(E2-e2);
de2dt = -k3F*e2*pr + (k3R+k4F)*(E2-e2) - k4R*p2*e2;
dp2dt = k4F*(E2-e2) - k4R*p2*e2;
f = [ds1dt; de1dt; dpldt; dprdt; de2dt; dp2dt];
end
tspan = 0:0.001:40;
initial = [1,1,0,0,1,0];
[t,x] = ode45( @dXdT, tspan, initial);

The concentration of the substitute, intermediate products and end product is plotted below:

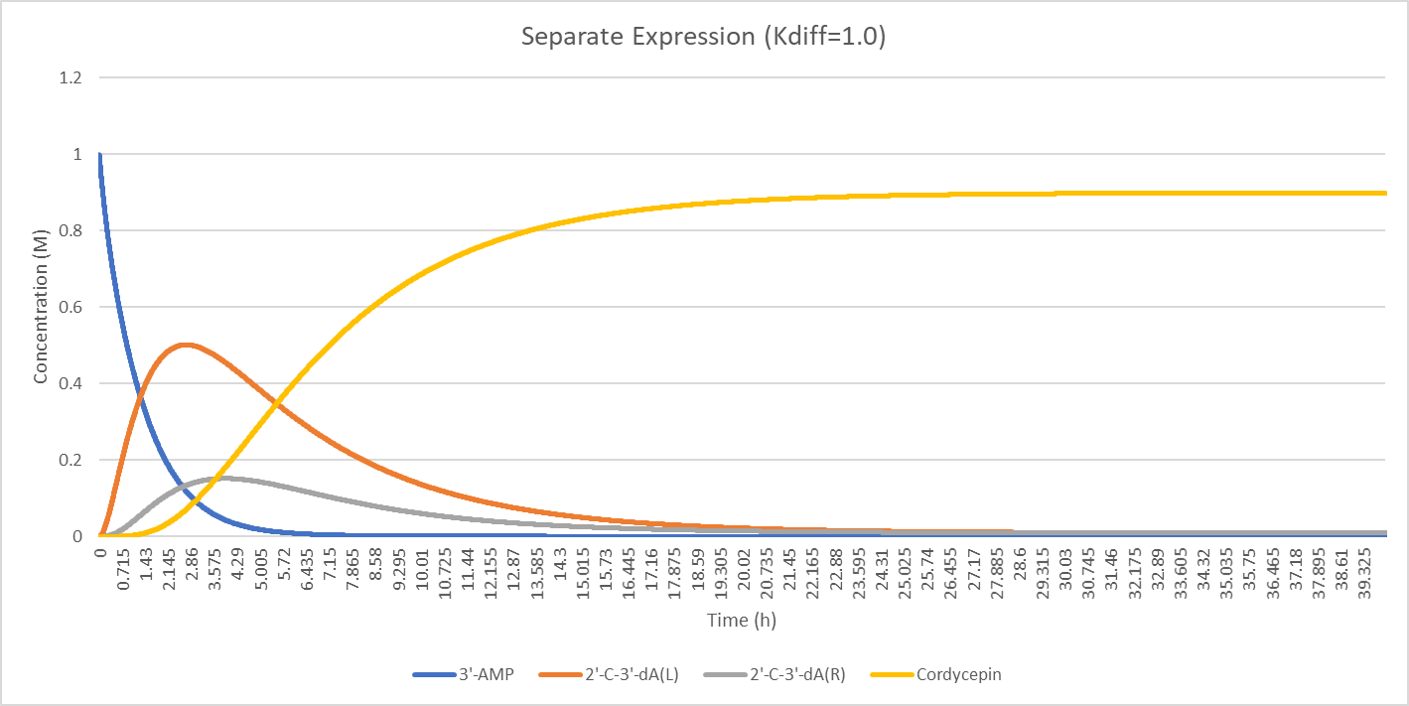
The figure above shows that the concentration of 2'-C'3'-dA is different after diffusion from that before diffusion. The peak of the orange line and grey line is also inconsistent. The peak of the grey line is slightly rightward to the peak of the orange line.

Furthermore, we would like to investigate the influence of the diffusion rate $k_\text{diff}$ on the concentration of the intermediate products and the end product.

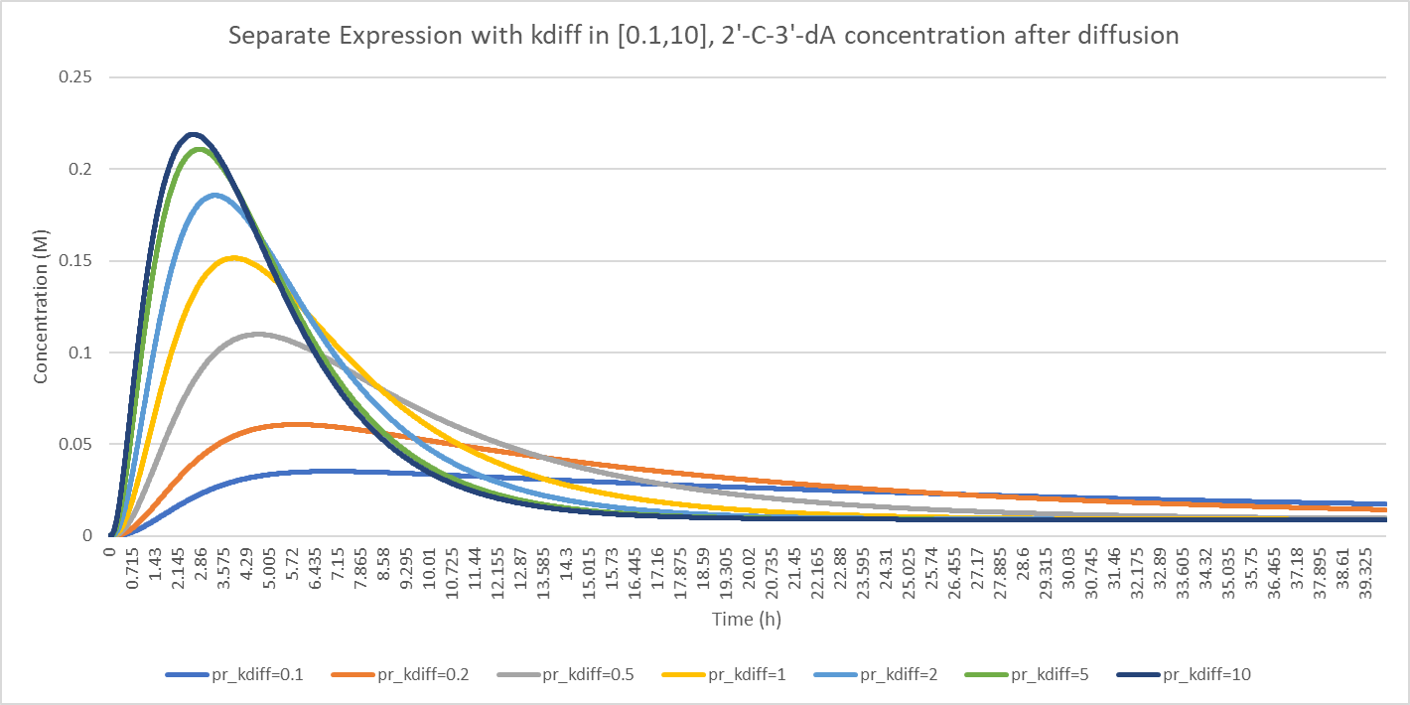
In the figure above, 2'-C'3'-dA concentration before diffusion shows a higher level when the diffusion rate is low, and it drops more quickly when the diffusion rate is high, resulting in a low concentration level. Reverse to the 2'-C'3'-dA concentration before diffusion, 2'-C'3'-dA concentration after diffusion presents increasing concentration level when the diffusion rate rises. These figures illustrate how diffusion influence the enzyme kinetics.

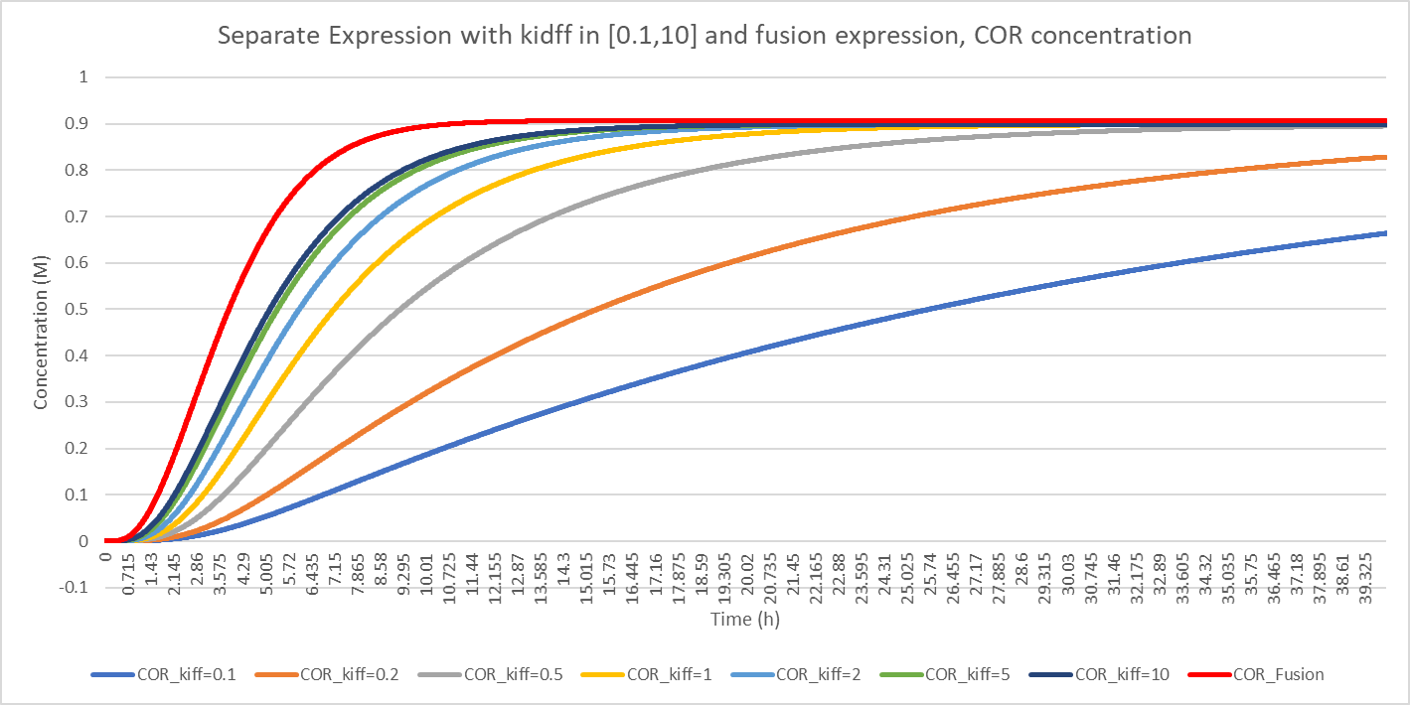
The concentration deviation of the end product cordycepin in relation to the increase of $k_\text{diff}$ suggests that the production efficiency raises when the diffusion rate increases, while the final conentration of the end product is the same value. The red line (cordycepin conentration of fusion-expression strategy) goes much more quickly than all other lines even that of the highest diffusion rate, 10. It is reasonable because fussion-expression strategy without diffusion is considered that $k_{diff} \to \infty$.

1.4.2 Separate Expression Simulation with abundant resource

Just as the manipulation of the fusion expression model, we set the concentration of the substitute $S_1$ to a constant. The result is below:

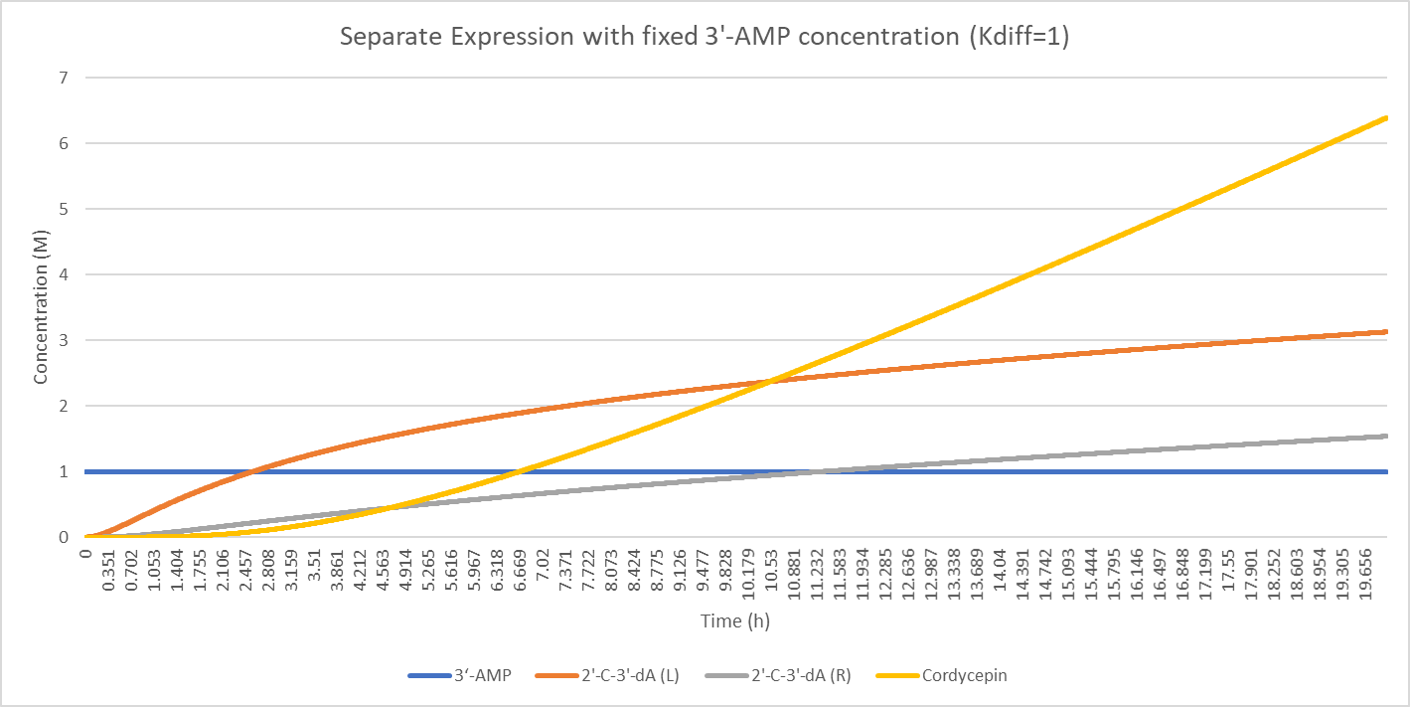
Different from the case when the resource is limited, all the products (including the intermediate products and end product) are increasing without any dropping tendency. The difference between 2'-C-3'-dA before and after diffusion becomes constantly bigger. After a while, the production of cordycepin is nearly a straight line.

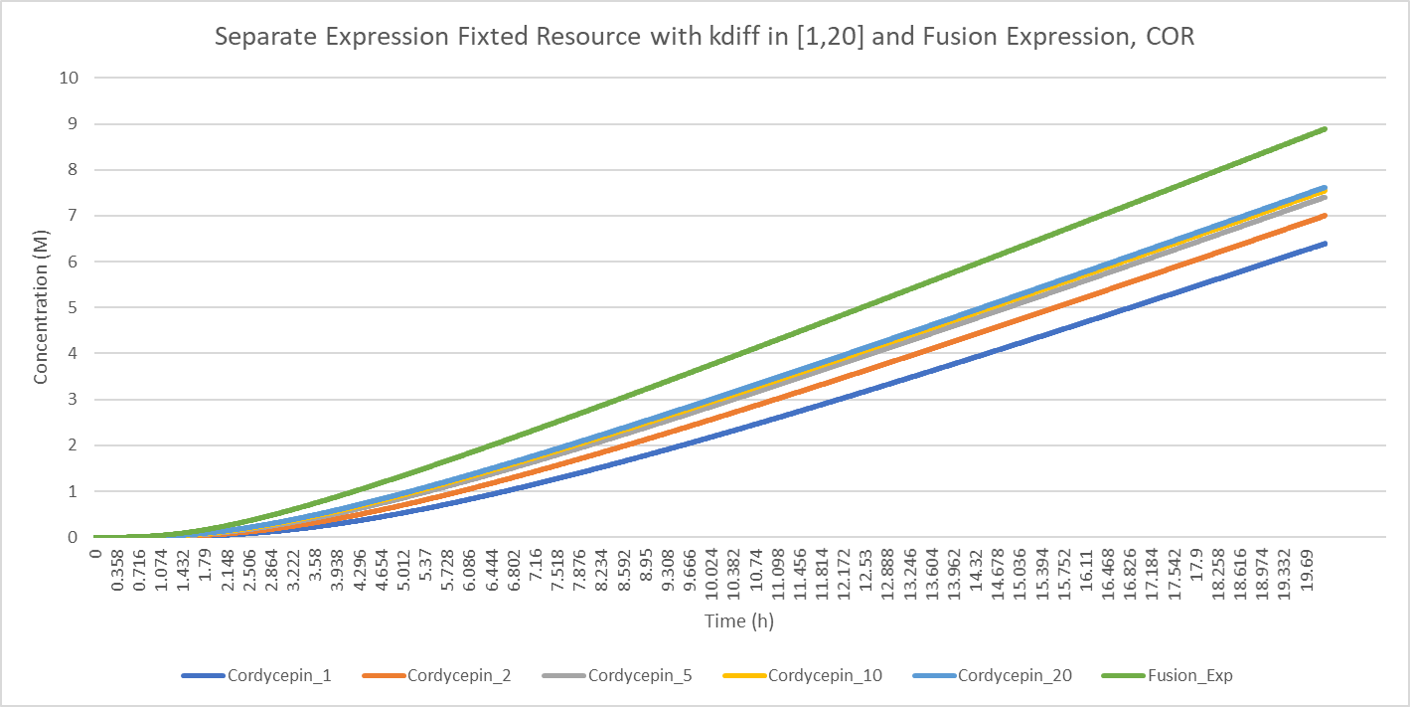
Considering the influence of $k_{diff}$ on the production of cordycepin and comparing the production of cordycepin under fusion-expression strategy and separate-expression strategy, we can derive the conclusion that the higher $k_{diff}$ is the higher production efficiency is.

1.5 Summary

The result of the separate expression model, both in limited resource and abundant resource, testifies that fusion-expression strategy, compared with separate-expression strategy, has a more efficient production of cordycepin.

Based on the model and the result, we prove the priority of fusion expression in theory by enzyme kinetic. This good result gives us strong confidence and support on the experiments of fusion expression of cns1 and cns2.

2 Systematic Enzyme Kinetics

In the fusion expression simulation, we discussed the catalytic process of cns1 and cns2, leaving alone the function of cns3 and its product pentostatin, which is an inhibitor to the adenosine deaminase (ADA). When we add the role of cns3-HisG domain and ADA, the systematic enzyme kinetics is represented by the following diagram.

In the diagram, product of cns1, $P_2$ (cordycepin), is deaminized to 3'-dI ($P_3$) by adenosine deaminase (ADA), which is the $E_{ADA}$ in the diagram. However, inhibitor (pentostatin), which is the $I$ in the diagram, can competitively inhibit the catalytic activity of ADA [Wu P et al. (2017)], [Li G et al. (2015)]. Pentostatin and ADA will from a complex, which is not functional and can not produce any substances.

2.1 Systematic Simulation with Limited Resource

As the cases in the above sections, we can derive the kinetic equations from the diagram.

$$\frac{d[S_1]}{dt} = -k_1[E_\text{cns2}][S_1] + k_{-1}[E_\text{cns2}S_1]$$

$$\frac{d[E_\text{cns2}]}{dt} = -k_1[E_\text{cns2}][S_1] + k_{-1}[E_\text{cns2}S_1] + k_2[E_\text{cns2}S_1] - k_{-2}[P_{1}][E_\text{cns2}]$$

$$\frac{d[E_\text{cns2}S_1]}{dt} = k_1[E_\text{cns2}][S_1] - k_{-1}[E_\text{cns2}S_1] - k_2[E_\text{cns2}S_1] + k_{-2}[P_{1}][E_\text{cns2}]$$

$$\frac{d[P_1]}{dt} = k_2[E_\text{cns2}S1]-k_{-2}[P_1][E_\text{cns2}]-k_3[E_\text{cns1}][P_1]+k_{-3}[E_\text{cns1}S_2]$$

$$\frac{d[E_\text{cns1}]}{dt} = -k_{3}[E_\text{cns1}][P_{1}] + k_{-3}[E_\text{cns1}S_2] + k_4[E_\text{cns1}S_2] - k_{-4}[P_2][E_\text{cns1}]$$

$$\frac{d[E_\text{cns1}S_2]}{dt} = k_3[E_\text{cns1}][P_{1}] - k_{-3}[E_\text{cns1}S_2] - k_4[E_\text{cns1}S_2] + k_{-4}[P_2][E_\text{cns1}]$$

$$\frac{d[P_2]}{dt} = k_4[E_\text{cns1}S_2] - k_{-4}[P_2][E_\text{cns1}] - k_5[E_\text{ADA}][P_2] + k_{-5}[E_\text{ADA}S_3]$$

$$\frac{d[E_\text{ADA}]}{dt} = -k_5[E_\text{ADA}][P_2] + k_{-5}[E_\text{ADA}S_3] + k_6[E_\text{ADA}S_3] - k_{-6}[P_3][E_\text{ADA}] - k_9[I][E_\text{ADA}] + k_{-9}[E_\text{ADA}I]$$

$$\frac{d[E_\text{ADA}S_3]}{dt} = K_5[E_\text{ADA}][P_2] - k_{-5}[E_\text{ADA}S_3] - k_6[E_\text{ADA}S_3] + k_{-6}[P_3][E_\text{ADA}]$$

$$\frac{d[P_3]}{dt} = k_6[E_\text{ADA}S_3] - k_{-6}[P_3][E_\text{ADA}]$$

$$\frac{d[S_4]}{dt} = -k_7[E_\text{HisG}][S_4] + k_{-7}[E_\text{HisG}S_4]$$

$$\frac{d[E_\text{HisG}]}{dt} = -k_7[E_\text{HisG}][S_4] + k_{-7}[E_\text{HisG}S_4] + k_8[E_\text{HisG}S_4] - k_{-8}[E_\text{HisG}][S_4]$$

$$\frac{d[E_\text{HisG}S_4]}{dt} = k_7[E_\text{HisG}][S_4] - k_{-7}[E_\text{HisG}S_4] - k_8[E_\text{HisG}S_4] + k_{-8}[E_\text{HisG}][I]$$

$$\frac{d[I]}{dt} = k_8[E_\text{HisG}S_4] - k_{-8}[E_\text{HisG}][S_4] - k_9[I][E_\text{ADA}] + k_{-9}[E_\text{ADA}I]$$

$$\frac{d[E_\text{ADA}I]}{dt} = k_9[I][E_\text{ADA}] - k_{-9}[E_\text{ADA}I]$$

Likewise, we can simplify this 14-equation system to 10-equation system because the initial concentrations of the enzymes are fixed. In the enzymes, $E_\text{ADA}$ is a little different, since the case that $[E_\text{ADA}] + [E_\text{ADA}S_3] + [EI] = E_\text{ini3}$, so $[E_\text{ADA}S_3]$ can be represented by $E_\text{ini3} - [E_\text{ADA}] - [EI]$.

Thus, the equations can be simplified to:

$$\frac{d[S_1]}{dt} = -k_1[E_\text{cns2}][S_1] + k_{-1}(E_\text{ini2}-[E_\text{cns2}])$$

$$\frac{d[E_\text{cns2}]}{dt} = -k_1[E_\text{cns2}][S_1] + (k_{-1}+k_2)(E_\text{ini2}-[E_\text{cns2}]) - k_{-2}[P_{1}][E_\text{cns2}]$$

$$\frac{d[P_1]}{dt} = k_2(E_\text{ini2}-[E_\text{cns2}])-k_{-2}[P_1][E_\text{cns2}]-k_3[E_\text{cns1}][P_1]+k_{-3}(E_\text{ini1}-[E_\text{cns1}])$$

$$\frac{d[E_\text{cns1}]}{dt} = -k_{3}[E_\text{cns1}][P_{1}] + (k_{-3}+k_4)(E_\text{ini1}-[E_\text{cns1}]) - k_{-4}[P_2][E_\text{cns1}]$$

$$\frac{d[P_2]}{dt} = k_4(E_\text{ini1}-[E_\text{cns1}]) - k_{-4}[P_2][E_\text{cns1}] - k_5[E_\text{ADA}][P_2] + k_{-5}(E_\text{ini3} - [E_\text{ADA}] - [EI])$$

$$\frac{d[E_\text{ADA}]}{dt} = -k_5[E_\text{ADA}][P_2] + (k_{-5}+k_6)(E_\text{ini3} - [E_\text{ADA}] - [EI]) - k_{-6}[P_3][E_\text{ADA}] - k_9[I][E_\text{ADA}] + k_{-9}[E_\text{ADA}I]$$

$$\frac{d[P_3]}{dt} = k_6(E_\text{ini3} - [E_\text{ADA}] - [EI]) - k_{-6}[P_3][E_\text{ADA}]$$

$$\frac{d[S_4]}{dt} = -k_7[E_\text{HisG}][S_4] + k_{-7}(E_\text{iniH}-[E_\text{HisG}])$$

$$\frac{d[E_\text{HisG}]}{dt} = -k_7[E_\text{HisG}][S_4] + (k_{-7}+k_8)(E_\text{iniH}-[E_\text{HisG}]) - k_{-8}[E_\text{HisG}][S_4]$$

$$\frac{d[I]}{dt} = k_8(E_\text{iniH}-[E_\text{HisG}]) - k_{-8}[E_\text{HisG}][S_4] - k_9[I][E_\text{ADA}] + k_{-9}[E_\text{ADA}I]$$

$$\frac{d[E_\text{ADA}I]}{dt} = k_9[I][E_\text{ADA}] - k_{-9}[E_\text{ADA}I]$$

MATLAB Code:

function [f] = dXdT(t, x)
k1F = 1;
k1R = 0.1;
k2F = 2;
k2R = 0.1;
k3F = 1;
k3R = 0.1;
k4F = 1;
k4R = 0.1;
k5F = 1;
k5R = 0.5;
k6F = 1;
k6R = 0.5;
k7F = 1;
k7R = 0.1;
k8F = 1;
k8R = 0.1;
k9F = 10;
k9R = 0.1;
E01 = 1;
E02 = 1;
E03 = 1;
E04 = 1;
s1=x(1);
e1=x(2);
p1=x(3);
e2=x(4);
p2=x(5);
e3=x(6);
p3=x(7);
s4=x(8);
e4=x(9);
i=x(10);
ei=x(11);
ds1dt = -k1F*e1*s1 + k1R*(E01-e1);
%dsdt = 0;
de1dt = -k1F*e1*s1 + (k1R+k2F)*(E01-e1) - k2R*p1*e1;
dp1dt = k2F*(E01-e1) - k2R*p1*e1 - k3F*e2*p1 + k3R*(E02-e2);
de2dt = -k3F*e2*p1 + (k3R+k4F)*(E02-e2) - k4R*p2*e2;
dp2dt = k4F*(E02-e2) - k4R*p2*e2 - k5F*e3*p2 + k5R*(E03-e3-ei);
de3dt = -k5F*e3*p2 + (k5R+k6F)*(E03-e3-ei) - k6R*p3*e3 - k9F*i*e3 + k9R*ei;
dp3dt = k6F*(E03-e3-ei) - k6R*p3*e3;
ds4dt = -k7F*e4*s4 + k7R*(E04-e4);
%ds4dt = 0;
de4dt = -k7F*e4*s4 + (k7R+k8F)*(E04-e4) - k8R*e4*s4;
didt  = k8F*(E04-e4) - k8R*e4*s4 - k9F*i*e3 + k9R*ei;
deidt = k9F*i*e3 - k9R*ei;
f = [ds1dt; de1dt; dp1dt; de2dt; dp2dt; de3dt; dp3dt; ds4dt; de4dt; didt; deidt];
end
tspan = 0:0.001:100;
initial = [1,1,0,1,0,1,0,2,1,0,0];
[t,x] = ode45( @dXdT, tspan, initial);

The result shows the concentration deviation of the substances involved.

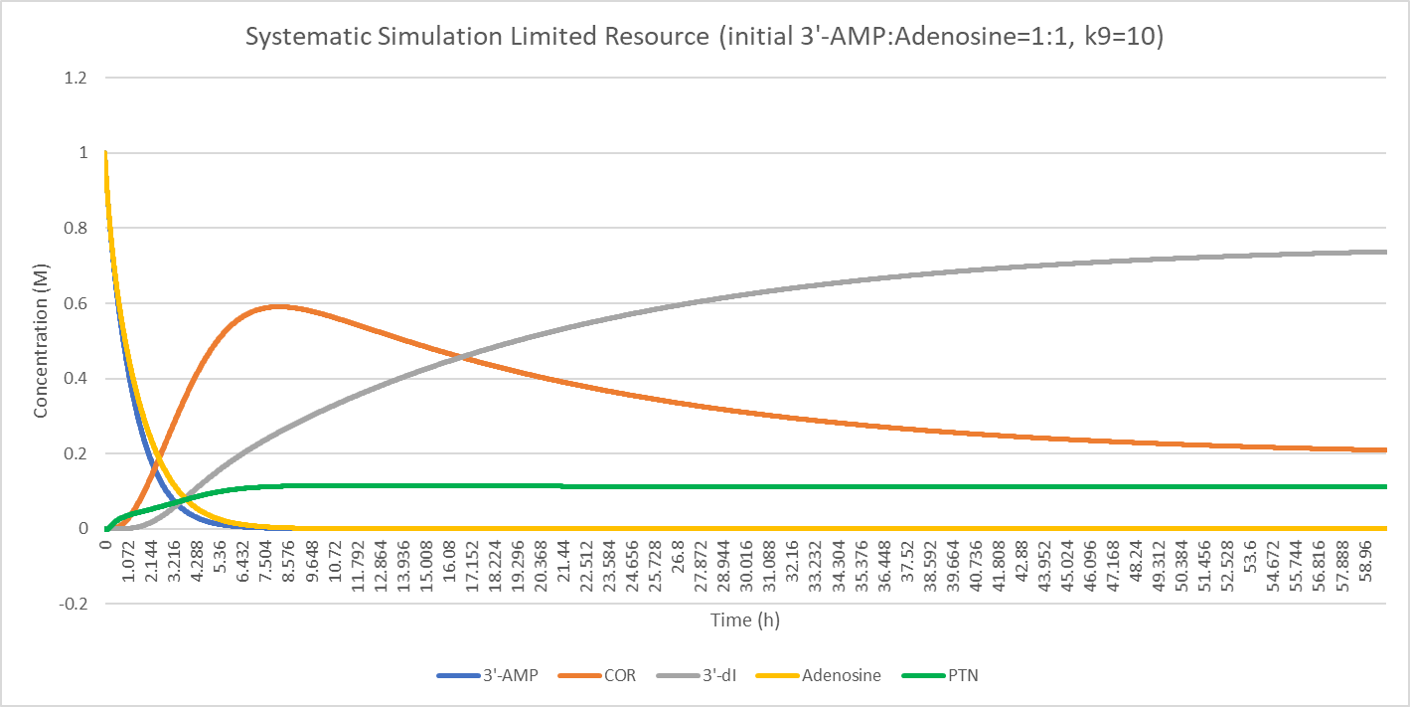
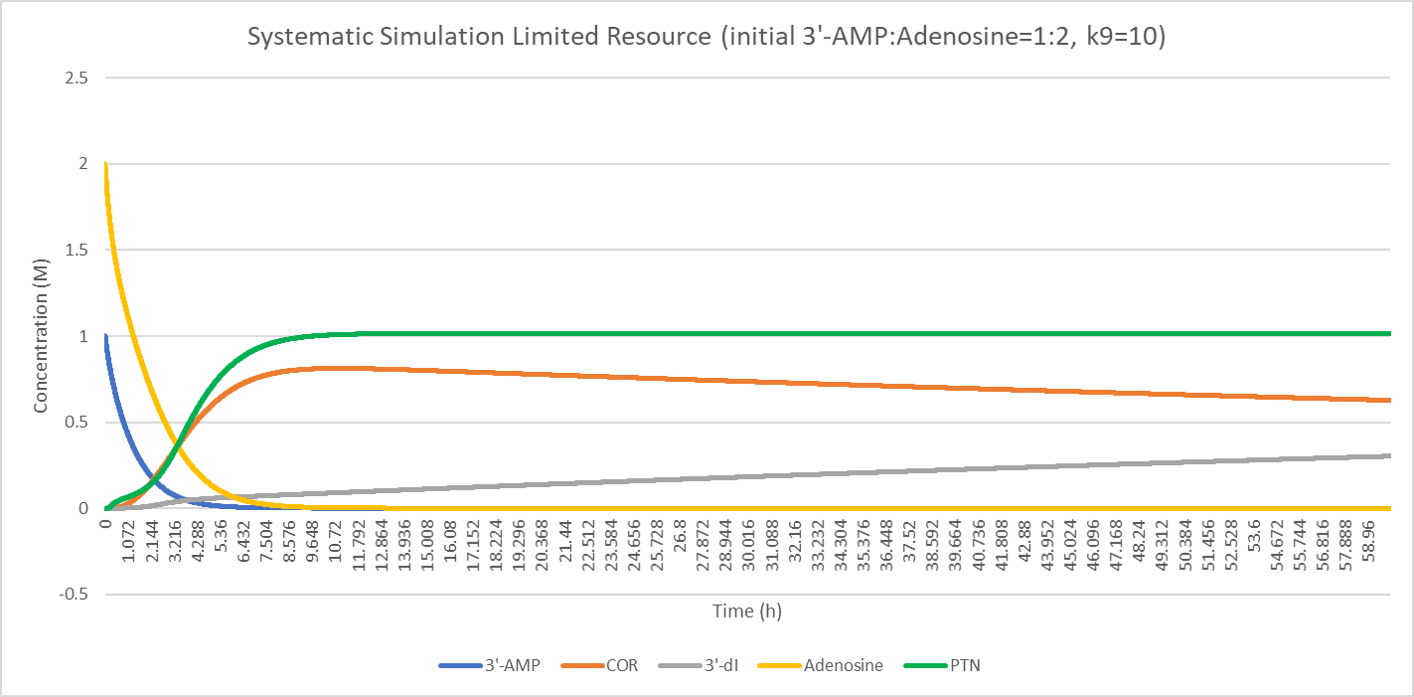
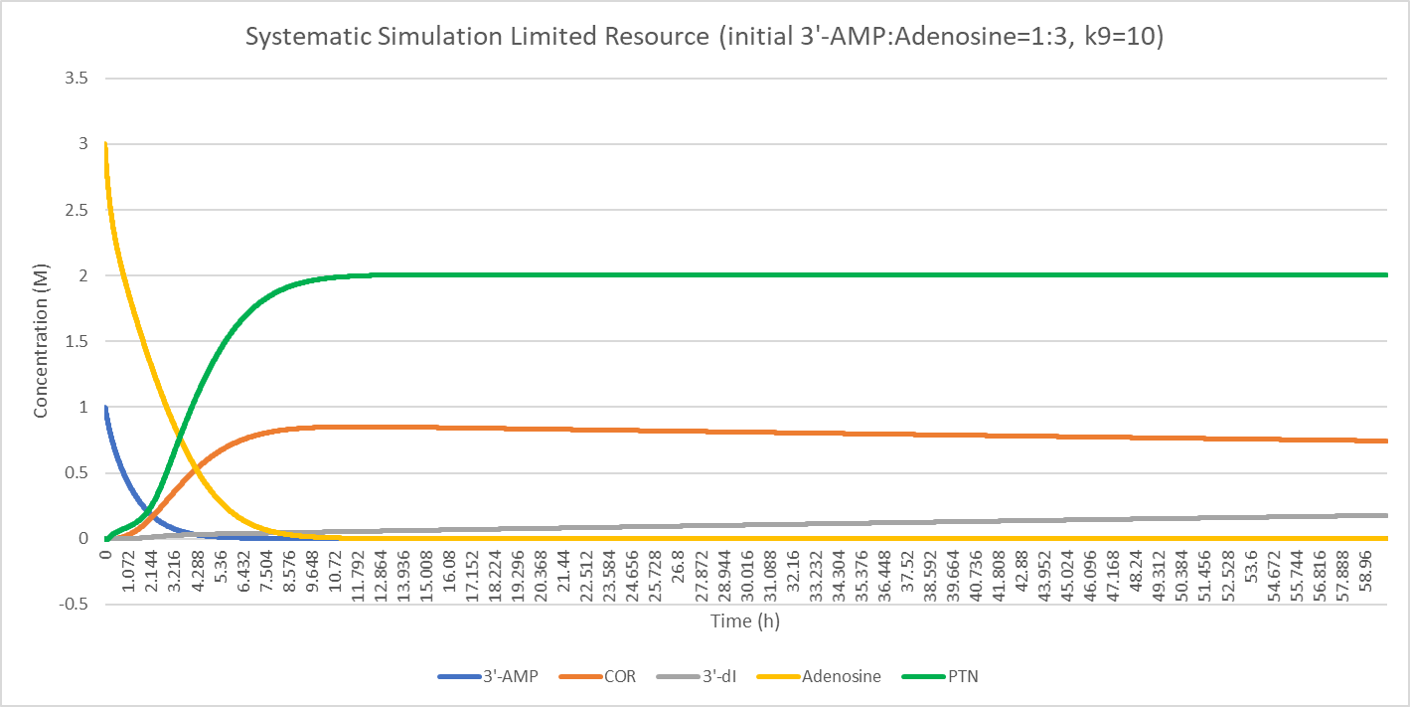
Comparison of the initial concentration of 3'-AMP (1, 2, 3 respectively) shows that when the resource is limited, equal concentration of cordycepin pentostatin will cause a fair part of cordycepin converting to nonfunctional product, 3'-dI. However, substitute ratio above 2:1 (3'-AMP: adenosine) will dramatically repress this conversion and enable more production of cordycepin.

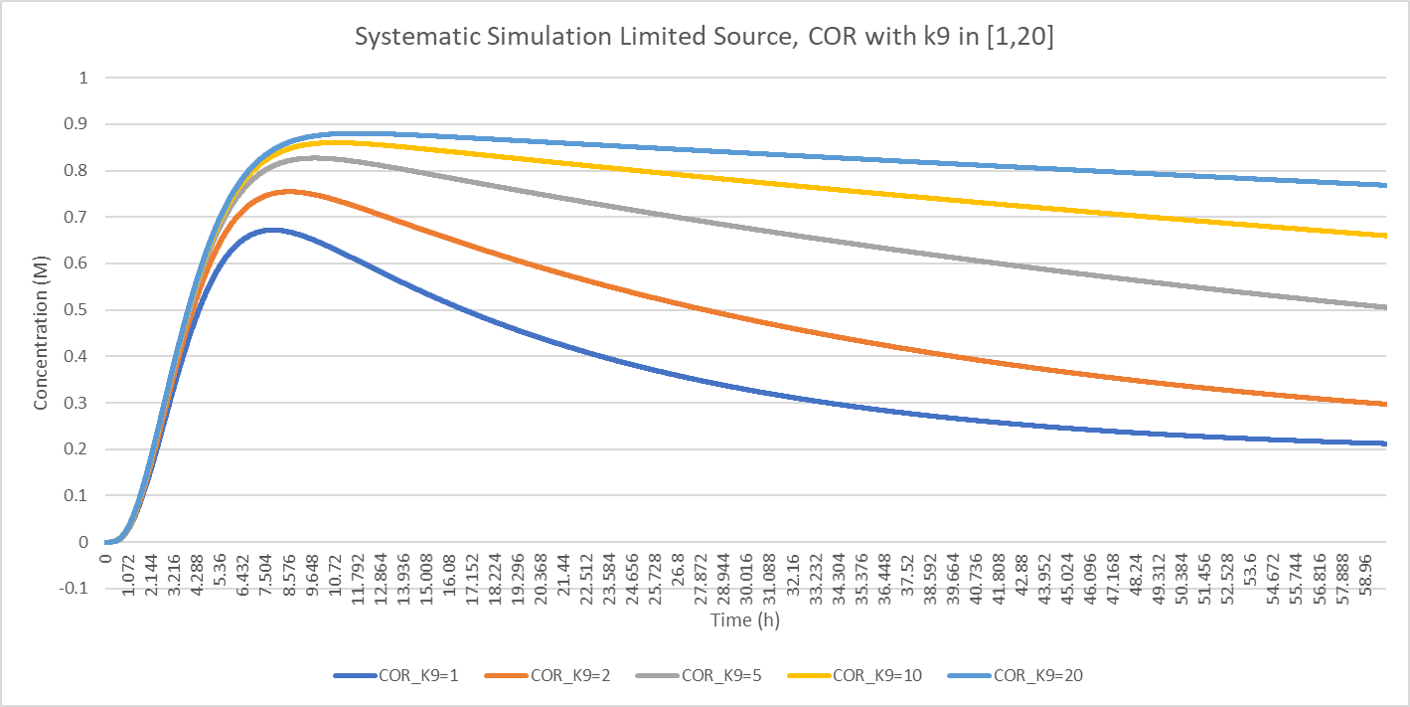
After the overall description of the model, we would like to evaluate the parameter of $k_9$, which is the reaction constant of the combination reaction of inhibitor and ADA, which is a kind of indicator for measuring the inhibition strength of pentostatin. From the figure, we can see that as the increase of $k_9$, the max COR production as peak goes up and the decrease is inhibited.

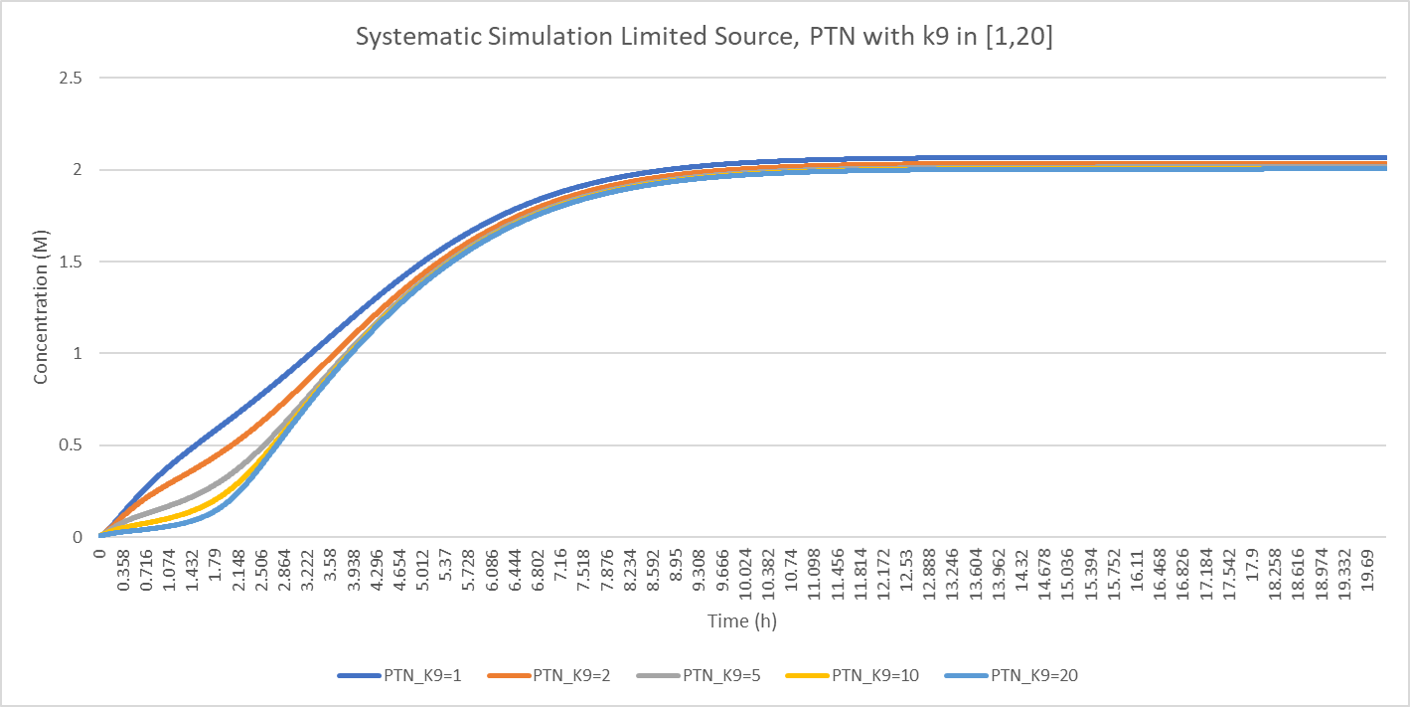
The influence of $k_9$ on PTN production is shown above, as the lines increase slower in initial stage when $k_9$ is higher. However, the producton level of PTN is nearly stationary.

The result gives us a conclusion that the best harvest time of cordycepin is slightly after the peak and the higher $k_9$ is, the slower conversion of cordycepin to nonfunctional product.

2.2 Systematic simulation with abundant resource

The substitutes in the system are $S_1$ (3'-AMP) and $S_4$ (adenosine), which would be constant with abundant resource.

$$\frac{d[S_1]}{dt} = 0$$

$$\frac{d[S_4]}{dt} = 0$$

Leaving other equations unchanged and we could get the result below.

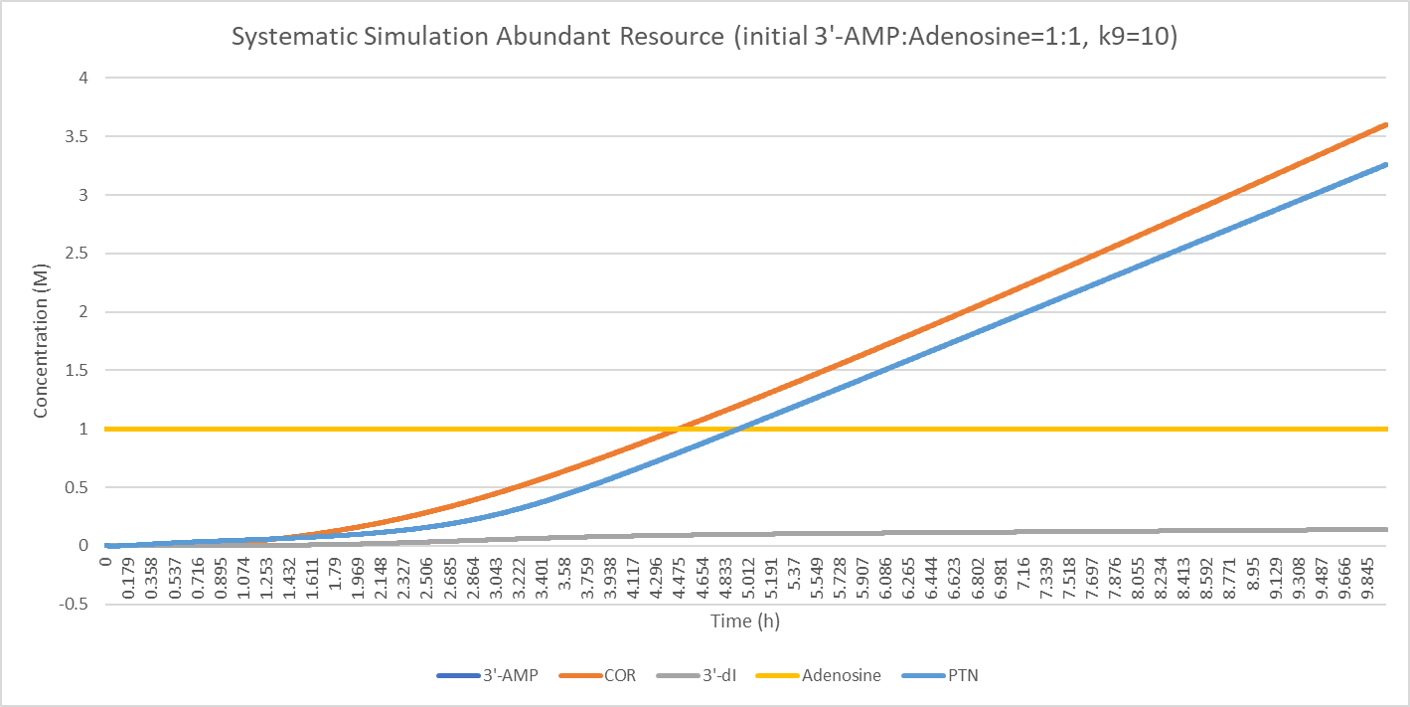
The result suggests that when the substitutes are abundant, the concentration of pentostatin will raise more quickly as time goes because the concentration of the inhibition complex ($E_\text{ADA}I$) amasses and it needs less inhibitor (pentostatin) to form the complex.

Additionally, we need to discuss the optional sustitute ratio ($\frac{[\text{3'-AMP}]}{[\text{adenosine}]}$) based on current parameters which enable the max production of cordycepin.

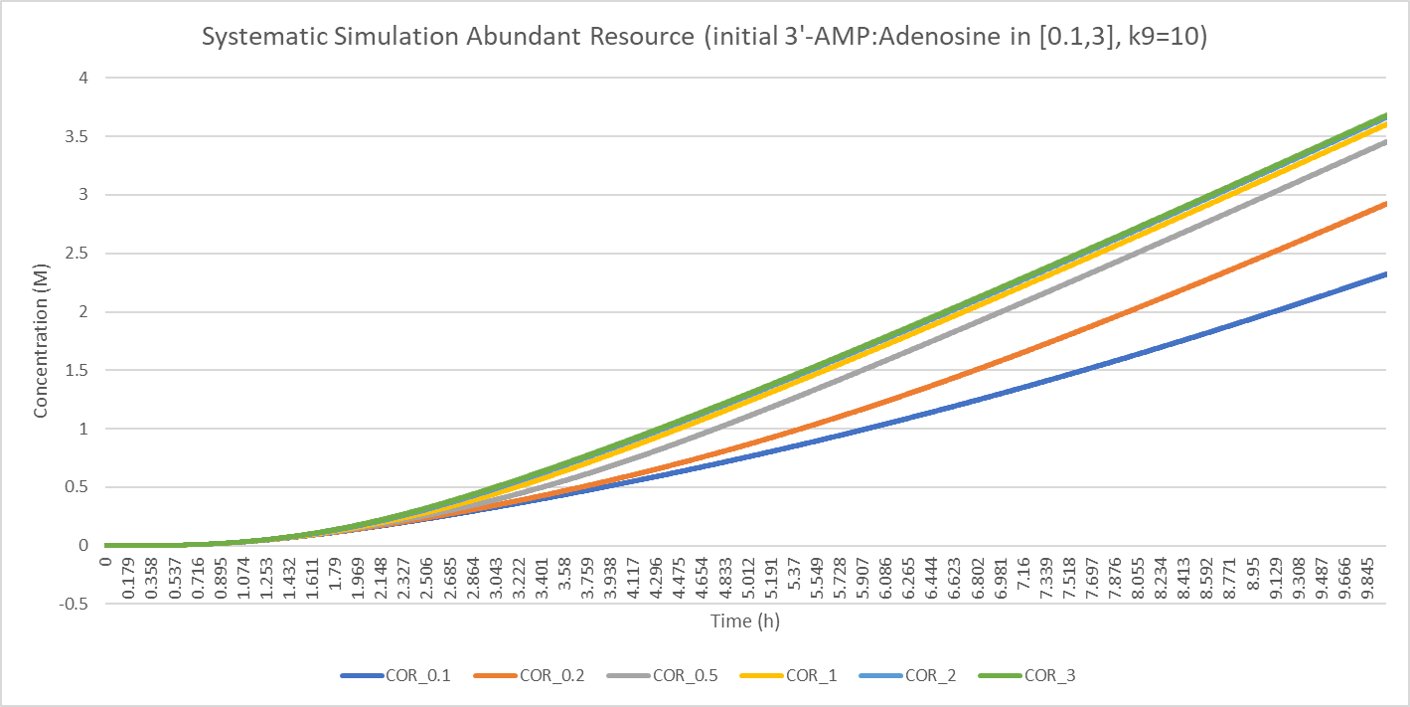
When we fixed the 3'-AMP concentration to 1M and the adenosine concentration to a set of values, 0.1, 0.2, 0.5, 1.0, 2.0 and 3.0, we plotted the figure above. In the figure, as the increase of initial adenosine concentration, the producing rate of cordycepin increases. The mechanism behind the result is that more pentostatin is produced with higher adenosine concentration and the conversion of cordycepin to 3'-dI is inhibited, resulting in more cordycepin remained.

The result above is reasonable, but meaningless, because we all know that more production of pentostatin will create more cordycepin. But what if we set a bound for total resource? In nature, the total energy of a cell at a time is limited although the energy can get supplemented by absorbing external resources. It is true that if a cell spends more energy in the production of cordycepin, it will spend less energy in pentostatin. Therefore, in the model, we set the sum of the concentration of 3'-AMP and adenosine to a fixed value and the two concentrations are stationary respectively. If we change the ratio between 3'-AMP and adenosine, the two concentrations will vary but the whole concentration is constant. Based on the manipulation above, we solve the equation system and get the following result:

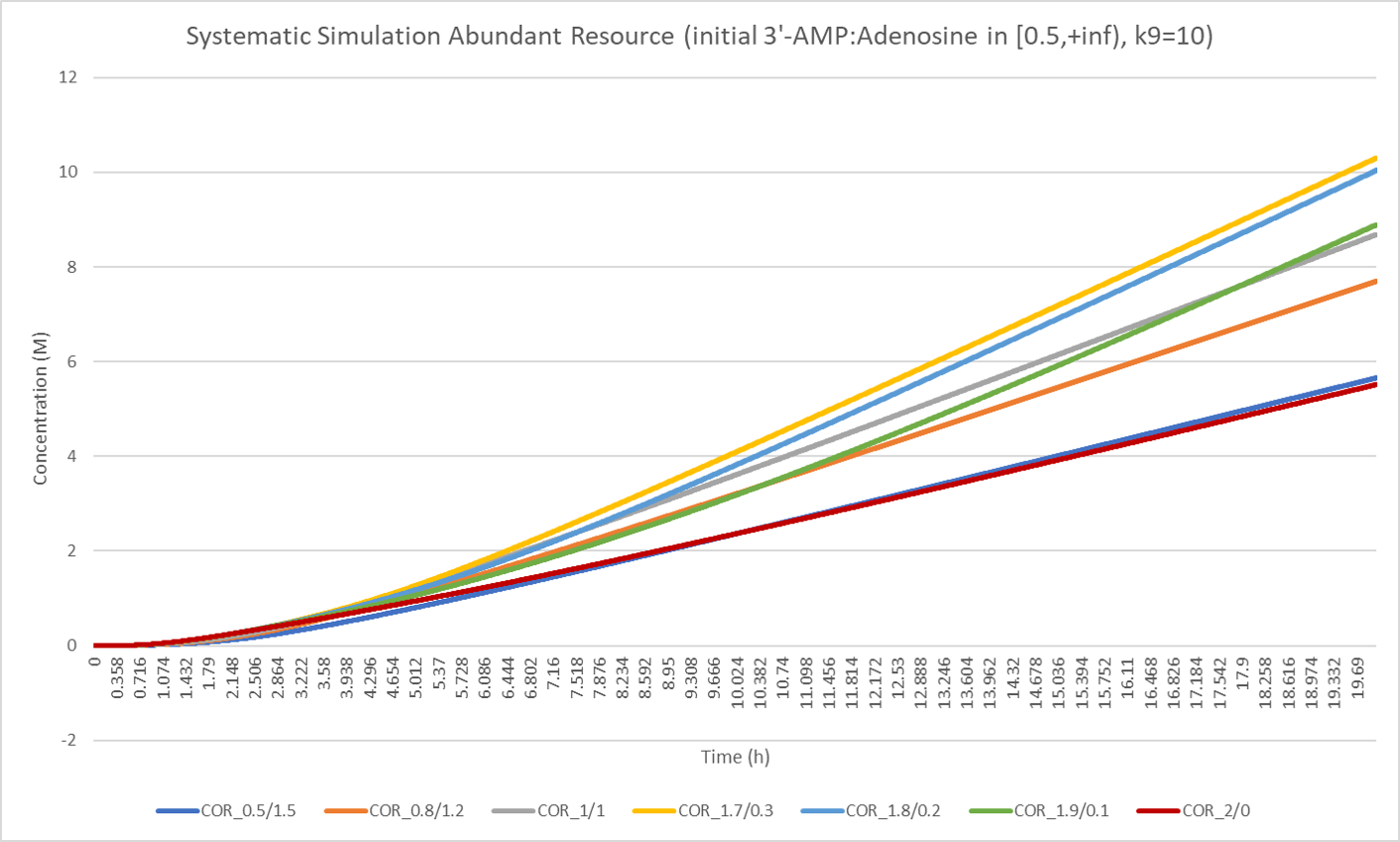
From the figure above, we can find that when the ratio between 3'-AMP and adenosine is below 1.7/0.3, high ratio will result in more cordycepin production efficiency. However, the case is inconsistent when the ratio exceeds 1.7/0.3. As the lines of the colors of light blue, green and blown, higher raio will generate lower production rate. In the extreme case, when adenosine is absent, the production of cordycepin will decrease to the level when the ratio is 0.5/1.5.

The result above gives us a clear illustration in theory that:
• Pentostatin does help promote the production of cordycepin.
• Appropriate ratio between the catalytic rate of cordycepin and pentostatin will result in the most production level of cordycepin. The raio can be adjusted by change of enzyme expression level if we have no access to changing the substitute level.

Since the goal of our project is to increase the efficiency and yield of cordycepin production, this result is helpful to the manufacturing. Although the parameters are set optional owing to lack of information, it will give a brief guideline of the optional ratio of cordycepin and pentostatin and will benefit the factories a lot when the enzymatic parameter is provided.

Appendix

Symbol list

Symbol	Description
[ ]	The concentration symbol
$S_1$	substitue adenosine
$E_{cns1}$	enzyme cns1
$E_{cns2}$	enzyme cns2
$E_{cns2}S_1$	enzyme-substitute complex of cns2 and $S_1$
$E_{cns1}S_2$	enzyme-substitute complex of cns1 and $S_2$
$P_{1Enol}$	product of enzyme cns1, which is in its enol form
$P_{1Keto-l}$	keto form of the product of cns2, at location of enzyme cns1
$P_{1Keto-r}$	keto form of the product of cns2, at location of enzyme cns2, after diffusion
$P_2$	product of enzyme cns1

Parameter list

Parameter	Description	Value	Reference
$k_1$	forward rate constant of cns2-S1 complex formation	1
$k_{-1}$	Reverse rate constant of cns2-S1 complex formation	0.1
$k_2$	forward rate constant of $P_{1Enol}$/$P_1$ product production	2
$k_{-2}$	reverse rate constant of $P_{1Enol}$/$P_1$ product production	0.1
$k_3$	forward rate constant of cns1-S2 complex formation	1
$k_{-3}$	Reverse rate constant of cns1-S2 complex formation	0.1
$k_4$	forward rate constant of $P_2$ product production	1
$k_{-4}$	reverse rate constant of $P_2$ product production	0.1
$k_5$	forward rate constant of $E_{ADA}S_3$ complex formation	1
$k_{-5}$	Reverse rate constant of $E_{ADA}S_3$ complex formation	0.5
$k_6$	forward rate constant of $P_{3}$ product production	1
$k_{-6}$	reverse rate constant of $P_{3}$ product production	0.5
$k_7$	forward rate constant of HisG-S4 complex formation	3
$k_{-7}$	Reverse rate constant of HisG-S4 complex formation	0.1
$k_8$	forward rate constant of $I$ product production	3
$k_{-8}$	reverse rate constant of $I$ product production	0.1
$k_9$	forward rate constant of $E_{ADA}I$ product production	10
$k_{-9}$	reverse rate constant of $E_{ADA}I$ product production	0.1

Reference

[Xia Y et al. (2017)]
Xia, Y. , Luo, F. , Shang, Y. , Chen, P. , Lu, Y. , & Wang, C. . (2017). Fungal cordycepin biosynthesis is coupled with the production of the safeguard molecule pentostatin. Cell Chemical Biology, S2451945617303276.

[Kozanecki M et al. (2016)]
Kozanecki, M. , Halagan, K. , Saramak, J. , & Matyjaszewski, K. . (2016). Diffusive properties of solvent molecules in neighborhood of polymer chain as seen by monte-carlo simulations. Soft Matter, 12(25), 5519.

[Huang L et al. (2007)]
Huang, L. , Huang, Y. , Chi, Y. , Lin, J. , Yu, L. , & Xu, L. , et al. (2007). Study on the kinetics of keto-enol tautomerism of p-hydroxyphenylpyruvic acid using capillary electrophoresis. Journal of Chromatography A, 1175(2), 283-288.

[Eun C et al. (2014)]
Eun, C. , Kekenes-Huskey, P. M. , Metzger, V. T. , & Mccammon, J. A. . (2014). A model study of sequential enzyme reactions and electrostatic channeling. The Journal of Chemical Physics, 140(10), 105101.

[Rice S et al. (1985)]
Rice, S. A. . (1985). Diffusion-limited reactions. Comprehensive Chemical Kinetics.

[Macheras P et al. (2006)]
Macheras, P. , & Iliadis, A. . (2006). Diffusion and Kinetics. Modeling in Biopharmaceutics, Pharmacokinetics, and Pharmacodynamics. Springer New York.

[M.H. Jacobs. (1935)]
M.H. Jacobs, Diffusion Processes, in: M.H. Jacobs (Ed.), Diffusion Processes, Springer Berlin Heidelberg, Berlin, Heidelberg, 1935, pp. 1-145.

[Wu P et al. (2017)]
Wu, P., Wan, D., Xu, G., Wang, G., Ma, H., Wang, T., ... & Li, Y. Q. (2017). An unusual protector-protégé strategy for the biosynthesis of purine nucleoside antibiotics. Cell chemical biology, 24(2), 171-181.

[Li G et al. (2015)]
Li, G., Nakagome, I., Hirono, S., Itoh, T., & Fujiwara, R. (2015). Inhibition of adenosine deaminase (ADA)‐mediated metabolism of cordycepin by natural substances. Pharmacology research & perspectives, 3(2), e00121.