统计学习方法 —— 感知机

机器学习

---

Elon Lin

---

定义

假设输入空间（特征空间）是 $\chi \subset R^{\ n}$，输出空间是 $\gamma = \{+1, -1\}$。输入 $x \in \chi$ 表示实例的特征向量，对应输入空间（特征空间）的点；输出 $y \in \gamma$ 表示实例的类别。由输入空间到输出空间的如下函数 :

$$f(x) = sign(w \cdot x + b)$$
称为感知机(perceptron)。

其中， $w$ 和 $b$ 为感知机模型参数，$w \in R^{\ n}$ 叫做权值（weight）或权值向量（weight vector），$b \in R^n$ 叫做 偏置(bias)， $w \cdot x$ 表示 $w$ 和 $x$ 的内积。$sign$ 是符号函数，即

$$sign(x)= \left\{ \begin{array}{ll}+1,& x \geq 0\\ -1,& x < 0 \end{array} \right.$$

假设空间 : 定义在特征空间中的所有线性分类模型(linear classification model) 或 线性分类器(linear classifier)，即函数集合$\{f \ | \ f(x) = w \cdot x + b\}$

感知机学习 : 由训练数据集（实例的特征向量与类别）

$$T = \{(x_1, y_1), (x_1, y_2), ..., (x_n, y_N)\}$$
求得感知机模型$f(x)$ 中的模型参数 $w, b$。

感知机预测 : 通过学习得到的感知机模型，对于新的输入实力给出其对应的输出类别。

感知机学习策略

数据集的线性可分性

给定一个数据集

$$T = \{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\},$$ 其中， $x_i \in \chi = R^{\ n}, \ y_i \in \gamma = {+1, -1}, \ i = 1, 2, ..., N$，如果存在某个超平面 $S$ :
$$w \cdot x + b = 0$$ 能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧，则称数据集 $T$ 为线性可分数据集(linear separable data set)

损失函数

假设训练数据线性可分，为了找到这个平面需要确定一个学习策略，即定义（经验）损失函数并将损失函数极小化

给定一个数据集

$$T = \{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\},$$ 其中， $x_i \in \chi = R^{\ n}, \ y_i \in \gamma = {+1, -1}, \ i = 1, 2, ..., N$。感知机 $sign(w \cdot x + b)$ 学习的 损失函数 定义为 :
$$L(w, b) = -\sum_{x_i \in M}y_i(w \cdot x_i + b)$$ 其中 $M$ 是误分类点的集合。

感知机学习的策略是在假设空间中选取是损失函数最小的模型参数$w, b$，即感知机模型。

感知机学习算法

感知机学习算法是对以下最优化问题的算法。给定一个数据集

$$T = \{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\},$$ 其中， $x_i \in \chi = R^{\ n}, \ y_i \in \gamma = \{+1, -1\}, \ i = 1, 2, ..., N$。求参数 $w, b$ 使其为以下损失函数 极小化 问题的解 $$minL(w, b) = -\sum_{x_i \in M}y_i(w \cdot x_i + b)$$ 其中 $M$ 为误分类点的集合。

感知机学习算法是误分类驱动的，具体采用随机梯度下降法(stochastic gradient descent)。首先任意选取一个超平面 $w_0, b_0$，然后用梯度下降法不断地极小化目标函数。

假设误分类点结合 $M$ 是固定的，那么损失函数 $L(w, b)$ 的梯度由

$$\nabla_wL(w, b) = -\sum_{x_i \in M}y_ix_i \\ \nabla_bL(w, b) = -\sum_{x_i \in M}y_i$$ 给出。

原始形式

极小化过程不是使 $M$ 中所有误分类点的梯度下降，而是一次随机选取一个误分类点使其梯度下降。假设随机选取误分类点 $(x_i, y_i)$，对 $w, b$ 进行更新 ：

$$w \leftarrow w + \eta y_ix_i \\ b \leftarrow b + \eta y_i$$ 式中 $\eta (0 < \eta \leq 1)$ 是步长，在统计学习中又称学习率(learning rate)。这样，通过迭代可以期待损失函数 $L(w, b)$ 不断减小，直到为了0.

感知机学习算法的原始形式

输入：训练数据集 $T = \{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\}$， 其中， $x_i \in \chi = R^{\ n}, \ y_i \in \gamma = \{+1, -1\}, \ i = 1, 2, ..., N$；学习率 $\eta(0 < \eta \leq 1)$

输出：$w, b$；感知机模型 $f(x) = sign(w \cdot x + b)$

1. 选取初值 $w_0, b_0$；
2. 在训练集中选取数据 $(w_i, y_i)$；
3. 如果 $y_i(w \cdot x_i + b) \leq 0$ $$w \leftarrow w + \eta y_ix_i \\ b \leftarrow b + \eta y_i$$
4. 转至 （2），直到训练集中没有误分类点。

算法收敛性

为方便描述将偏置 $b$ 加入权重向量 $w$，记作 $\hat{w} = (w^{\ T}, b)^{\ T}$，同样将输入向量加以扩充，加进常数 $1$，记作 $\hat{x} = (x^T , 1)^T$。这样， $\hat{x} \in R^{\ n+1}, \hat{w} \in R^{\ n+ 1}$。显然， $\hat{w} \cdot \hat{x} = w \cdot x + b$

Novlkoff 定理

设训练集

$$T = \{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\},$$ 其中， $x_i \in \chi = R^{\ n}, \ y_i \in \gamma = \{+1, -1\}, \ i = 1, 2, ..., N$， 则
1. 存在满足条件 $\|\hat{w}_{opt}\| = 1$ 的超平面 $\hat{w}_{opt} \cdot \hat{x} = w_{opt} \cdot x + b_{opt} = 0$ 将训练数据集完全正确分开：且存在 $\gamma > 0$，对所有 $i = 1, 2, ..., N$ $$y_i(\hat{w}_{opt} \cdot \hat{x}_i) = y_i(w_opt \cdot x_i + b_{opt}) \geq \gamma$$
2. 令 $R = \max \limits_{1 \leq i \leq N}\|\hat{x}_i\|$，则感知机算法原始形式在训练数据集上的误分类次数k满足不等式 $$k \leq (\frac R \gamma)^2$$

定理表明，误分类次数是有上界的，经过有限次搜索可以找到将训练数据完全正确分开的分离超平面。即数据可分时，感知机学习算法原始形式迭代收敛，但训练集线性不可分时，干主机学习算法不收敛，迭代结果会发生震荡。

对偶形式

对偶形式的想法是，将 $w 和 b$ 表示为实例 $x_i$ 和标记 $y_i$ 的线性组合的形式，通过求解其系数而求得 $w 和 b$。不失一般性，可假设原始形式中初始值 $w_0, b_0$ 均为 $0$。对误分类点 $(x_i, y_i)$ 通过

$$w \leftarrow w + \eta y_ix_i \\ b \leftarrow b + \eta y_i$$ 逐步修改 $w, b$，设修改 $n$ 次，则 $w, b$ 关于 $(x_i, y_i)$ 的增量分别是 $\alpha_iy_ix_i 和 \alpha_iy_i$，这里 $\alpha_i = n_i\eta$。最后得到的 $w, b$ 可以分别表示为 $$w = \sum_{i = 1}^N\alpha_iy_ix_i \\ b = \sum_{i = 1}^N\alpha_iy_i$$
这里， $\alpha_i \geq 0, i = 1, 2, ..., N$

感知机学习算法的对偶形式

输入：线性可分的数据集 $T = \{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\}$，其中 $x_i \in \textbf{R}^N， y_i \in {-1, +1}, i = 1, 2, ..., N$；学习率 $\eta(0 < \eta \leq 1)$

输出：$\alpha, b$；感知机模型 $f(x) = sign(\sum_{j = 1}^N\alpha_jy_jx_j \cdot x + b)$
其中 $\alpha = (\alpha_1, \alpha_2, ..., \alpha_N)^T$

1. $\alpha \leftarrow 0, b \leftarrow 0$
2. 在训练集中选取数据 $x_i, y_i$
3. 如果 $y_i(\sum_{j = 1}^N\alpha_jy_jx_j \cdot x_i + b) \leq 0$ $$\alpha_j \leftarrow \alpha_j + \eta \\ b \leftarrow b + \eta y_i$$
4. 转至 2 直到没有误分类数据

对偶形式中，可以预处理训练集中实例间的内积并以矩阵存储，该矩阵即 Gram 矩阵(Gram matrix)

$$G = [x_i \cdot x_j]_{N \times N}$$

习题

1. Minsky 和 Papert 指出：感知机因为是线性模型，所以不能表示复杂的函数，如异或(XOR)。验证感知机为什么不能表示异或

   已知异或表示对于同一集合的两个元素(a, b)，a和b相同则为0， 相异则为1，由此可以得到其运算关系:

   • (0, 0) = (1, 1) = 0
   • (0, 1) = (1, 0) = 1
     可得图像 :
     
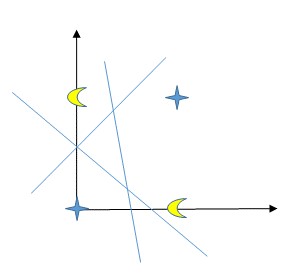
     由图像可以看出，XOR的训练集线性不可分，而感知机模型并不能学习线性不可分函数(linear insparable function)

2. 证明以下定理：样本集线性可分的充分必要条件是正实例点集所构成的凸壳与负实例点所构成的凸壳互不相交。

   必要性： 假设样本集T线性可分，则存在一个超平面 $w_{opt}$ 将数据集的正实例点和负实例点完全正确地划分到 $w_{opt}$ 的两侧。显然两侧的点分别构成的凸壳不相交；
   充分性： 假设存在两个凸壳A、B相交，且存在超平面 $w$ 将A和B线性分割。令A在B的凸壳内部的点为a，因为线性可分，则A中不存在两点之间的连线与超平面 $w$ 相交，而凸壳B中任意一点与A中的点的连线均与超平面 $w$ 相交，则B内部的点a也与A中任一点之间的连线不与 $w$ 相交，与A中不存在两点之间的连线与超平面小脚矛盾。故只有正负实例点所构成的两个凸壳不相交时样本集才线性可分。