卷积神经网络入门

原文 : A Beginner's Guide To Understanding Convolutional Neural Networks

翻译 : Elon Lin

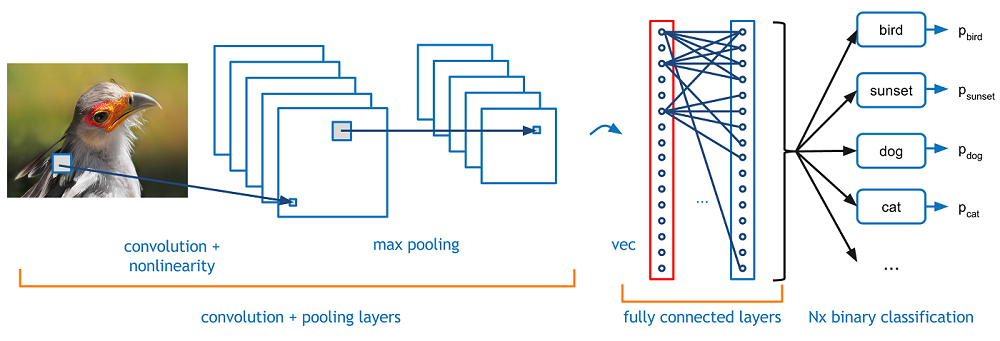
引入

卷积神经网络(Convolutional neural networks)。听起来就像是生物加数学在再计算机科学为佐料做成的一个狂野的组合，但这些网络却是计算机视觉领域极富有影响力的一部分创新。2012年是神经网络大放异彩的第一年，因为Alex Krizhevsky在2010年的ImageNet竞赛（计算机视觉领域每年一度的奥利匹克）利用它将分类错误率从26%降到了15%，这在当时是一个很大的提升。从那以后，许多公司都开始将深度学习应用在他们服务的核心部分。Facebook使用神经网络来做自动标记的算法，Google则将它应用到了他们的图片搜索，Amazon的产品推荐，Pinterest的主页反馈个性定制(home feed personalization)，Instagram的基础搜索功能等。

然而，这些网络最经典，最广泛应用的方面还是图像处理。在图像处理方面，我们可以看看CNN是如何应用到图像分类中的。

问题概述

图像分类是指这样一种工作，它将输入一个图片然后输出一个类别（猫，或者狗等等的）或者是一个可以描述这个图片的大致的类别。对于人类来说，这种识别技能是我们从出生以来学习的第一个技能之一，并且成年之后变得更加轻而易举。甚至不需要思考第二次， 我们也可以迅速并且完美地识别出我们周围的环境和周围的物体。当我们在看一张图片或者环顾四周的时候，很多时候我们都可以立即对场景做出描述并给每一个物体一个对应的标签，升值不需要刻意去观察。这种快速识别模式，开拓已知的知识，以及适应不同视觉环境的技巧是我们无法与我们造出的机器分享的东西。

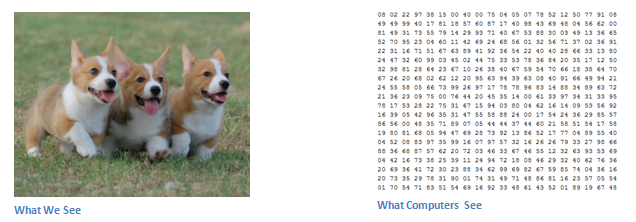
输入输出

当计算机在看一张图片时(用一张图片作为输入)，它看到的是一个像素值的阵列。它可能会看到一张 $32 \times 32 \times 3$ （3表示RGB的值）的数字阵列，这依赖于图片的分辨率和大小。简单地说，假设我们我们有一个大小为 $480 \times 480$ 的JPG格式有色图片，那么这个数字阵列的大小就是 $480 \times 480 \times 3$。这个阵列中的每一个数字都用0到255来代表当前像素强度。这些数字在我们做分类的时候是无意义的，但这是计算机唯一可行的输入方式。这个过程就是你给计算机输入这个数字阵列，然后它会输出一个数字用于描述这个图片对应特定类别的概率(例如 猫0.80，狗0.15，鸟0.05，等)

我们希望计算机做什么?

我们知道了问题和输入输出，现在我们来想想如何解决这个问题。我们需要计算机做的就是区分所有给出的图片，并且计算出独特的特征以便让一张狗的图片识别为狗，猫的图片识别为猫。这也是我们潜意识中进行的过程。当我们在看一张狗的图片时，如果这个照片有像爪子和四条腿这样的非常容易识别的信息，那么我们就可以很容易地分辨出来。也就是说，电脑有能力通过寻找低级的特征例如边界和曲线等，然后通过一些列的卷积层建立起更加抽象的概念。这就是CNN的一个大概的描述。近些来让我们来研究它的细节。

生物连接

首先是一点小的背景知识。当你第一次面对卷积神经网络的概念时，你也许会联想到生物学上的神经科学，某种程度上你猜对了。CNN确实从大脑的视觉皮层挑取了一些灵感。视觉皮层有一块细胞区域对看到的场景中的特定区域非常敏感。这个想法在1962年被Hubel和Wiesel通过一场有趣的实验进一步拓展，他们展示了一些大脑里的一些视觉神经细胞只会对场景中特定方向的边有反应。Hubel和Wiesel发现所有这些神经元都被集成在一个柱状的结构中，他们一起产生了视觉。一个系统中特定组成部分拥有特定的任务（视觉皮质中的神经元细胞寻找视觉场景中特定的特征）这种想法也是应用到机器应用的想法之一，当然也是CNN的基础。

结构特点

回到图像识别的特例上来。一个关于CNN更加详细的概括就是，你拿到一幅图像，把它扔到一系列构成卷积的、非线性的、池化的（降采样的）并且完全连接起来的层次中，得到一个输出。就像我们之前说的，这个输出结果可以是最符合这个图像的单个类别或者一堆类别的概率表示。现在，最难以理解的部分就是这些层次中的每一层都做了什么。那么我们进入最重要的一部分。

第一层 ： 数学部分

一个CNN网络的第一层一般是卷积层(Convolutional Layer， conv层)。你应该知道的第一件事是conv层的输入是什么。我们之前提到过，输入是一个 $32 \times 32 \times 3$ 的像素值数组（阵列）。现在，解释conv层最好的方法就是想象有一道闪光在这个图像的左上方闪过。这个闪光覆盖了一个 $5 \times 5$ 的区域。然后，想象这道闪光开始在这个输入的图象上滑动。在机器学习的术语中，这个闪光叫做过滤器(filter)（有时也叫一个神经元(neuron)或者一个核(kernel)），闪光着凉的区域叫做可接受区域(receptive field)。这个过滤器也是一个数字组成的数组（里面的数字叫做权重(weight)或参数(parameters)）。一个非常重要的点就是过滤器的深度(第三个维度的大小，译者注)和输入的深度相同（这保证数学计算正常），所以过滤器的大小就是 $5 \times 5 \times 3$。现在我们以过滤器所处的第一个位置为例，即左上角。当过滤器开始在图象上滑动，或者说卷积(convolving)时，它用过滤器矩阵去乘以图像上的像素点矩阵（对应位置相乘），然后相加(数学上讲，总共有75次乘法)，得到一个数字。记住，这个结果只代表图像左上角的那一部分。接下来，我们对输入矩阵的每一个位置都重复这个过程，即每一次将过滤器向右移动一个单位。这个输入矩阵的每一个位置都会得到一个结果值。过滤器在走完所有位置后得到一个 $28 \times 28 \times 1$ 的数字矩阵，被称为active map或feature map。之所以得到的是一个 $28 \times 28$ 的矩阵是因为一个 $5 \times 5$的方块在一个 $32 \times 32$的图上只有784个可能的位置，这784个数映射为一个 $28 \times 28$的矩阵。

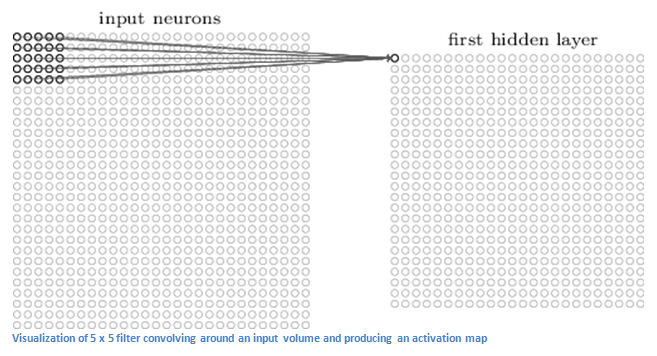
（PS：包括上面这幅图的一些图像都来源于 Michael Nielsen写的这本书籍 : Neural Networks and Deep Learning）

如果我们使用两个 $5 \times 5 \times 3$ 的过滤器而不是一个，那么我们得到输出就是一个 $28 \times 28 \times 2$ 的矩阵。通过使用更多的过滤器，我们可以更好地保护空间维度。从数学上讲， 这就是一个卷积层所做的事情。

第一层 ： 高级部分

不管怎样，让我们从更高层次上来说一下卷积到底做了什么。每一个过滤器都可以被认为是特征识别器。当我说到特征时，我说的是东西是指直线、单色、和曲线等。想一想每一个图像都具有的最简单的特征是什么。我们现在要用的是一个 $7 \times 7 \times 3$ 的过滤器，也是一个曲线探测器。（为了方便说明，这个部分我们忽略这个过滤器有3个单位的深度而只考虑过滤器和图像最上面的那一片）。作为一个曲线探测器，这个过滤器有一个由较高数字值构成的像素点的结构，它在整个过滤器的区域中形成一个曲线的形状（记住，我们说的过滤器只是一堆数字）。

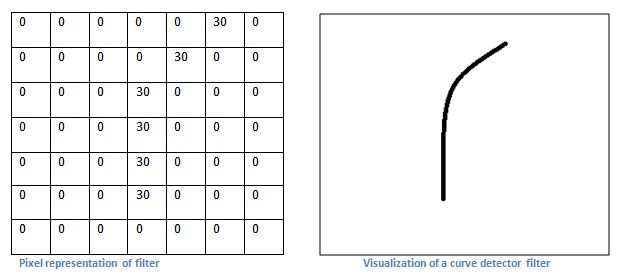
现在我们退回去看，当我们把过滤器放在图片的左上角时，便开始计算过滤去和这个区域像素值之间对应的乘积。现在我们拿一章我们想要匹配的图片，并且把过滤器放在左上角。

我们所要做的就是将过滤器和对应区域的数值对应相乘。

从以上结果我们可以看出，如果有一部分形状和过滤器所表示的曲线大体相同，那么所有相乘的结果之和将会得到一个很大的值。现在我们移动过滤器看看。

这个结果变得非常小。这是因为图像的这个部分没有任何一点和过滤器相吻合。记住，conv层的输出是一个活动图(activation map)。所以，在一个单过滤器卷积（并且这个过滤器是一个曲线探测器）的情况下，这个活动图展示了在图片中哪些区域最有可能有对应的曲线。在这个例子中，这个 $28 \times 28 \ times 1$ 的活动图的左上角的数值达到了6600。如此高的数值意味着这个区域存在某种曲线可以引起过滤器的“兴奋”，而活动图右上角的数值为0说明输入体的这个区域并引起过滤器的“兴奋”（更简单地说，原始图像中的这个区域并没有对应曲线）。记住，这只是对应一个过滤器。这只是一个发现一条向外凸起并向右延伸的曲线的一个过滤器。我们也可以有其他的向左延伸的或者探测直线的过滤器。过滤器越多，活动图的深度（第三维）越深，也就能得到更多的有关输入体的信息。

免责声明：我在这个部分所描述的过滤器是为了更简单地说明数学是如何应用在卷积过程中的。在下面这张图片中，你看到的是一个经过训练的网络的第一个conv层中的过滤器的可视化图像。尽管变成了这个样子，但它的主要参数仍然相同。第一层的过滤器卷积整个图片并且在匹配到特定特征时表现出“兴奋”（或者说计算的高一个较大值）

（PS ： 上图来源于斯坦福Andrej Karpathy 和 Justin Johnson 教授的课程 CS 231N course。推荐给想要进一步学习CNN的人们）

深入了解网络

在一个传统的卷积神经网络结构中，在这些conv层之间还散步这其他的一些层。我强烈建议有兴趣的人可以进一步阅读了解他们的作用和影响，但是为了简单说明，它们通过提供非线性因素和保存维度特征来提高网络
的鲁棒性以及防止过拟合。一个典型的CNN的结构和下面类似。

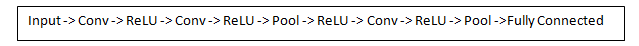
最后一层是我们之后要讲的很重要的一部分。现在我们回顾一下我们已经了解了多少。我们说到了第一个conv层中的过滤器是如何被设计用来探测的。它们可以发现低层次中边和曲线之类的特征。可以明了的是，为了预测一幅图片是是否是某一类对象，我们需要这个网络发现像爪子或者耳朵一类的高层次特征。现在我们来处理经过第一个conv层后的输出结果。那是一个 $28 \times 28 \times 3$ 的矩阵（假定过滤器是 $5 \times 5 \times 3$ 的话）。当第一层所有计算结束得到输出后进入第二个conv层，第一层的输出是第二层的输入。这个有点难想。对于第一层，它的输入就是原始图像。对于第二层来说，它的输入就是第一层生成的活动图。也就是说，每一个层的输入都是用来描述确定的低级特征在原本图像中出现的位置的。当经过一系列过滤器的应用之后，它的输出就是就是高一级的特征。典型的例子比如半圆(由一条曲线和直线构成)或者矩形(多条直线构成)。当你在穿越网络也就是穿过更多的conv层的时候，你就能得到代表着更加复杂特征的活动图。在网络的最后，你可能得到的是一些不同的过滤器，一些可以识别图片中的手写文字，或者是识别粉色物体等等的。如果你想了解更多卷积网络中可视化过滤器的，Matt Zeiler 和 Rob Fergus 有一篇 research paper 是讨论这个主题的。Jason Yosinski 在Youtube上也有一个视频展示了更好的可视化的内容。更加有趣的是，当越来越深入网络时，过滤器也拥有了越来越大的可处理范围，也就是说它们逐渐可以处理从原本输入中很大的一块区域中获得的信息（换句话说就是后期的网络对大范围的像素点会更有反应）

全连接层

现在我们来探索高层次的网络的作用，其中一个个就是接近网络末端的全连接层。这一藏当然也需要输入数据（就是在它之前的conv层或者ReLU层或者poor层的输出）并且输出一个N维的向量，其中N是程序选择让的分类的数量。例如，如果你做的是一个数字识别的程序，那么N就是10因为只有10个数字。在这个N维向量中的每一个数字代表的是一个确定类别的概率。例如，一个数字分类程序的返回结果可能是 [0, 0.1, 0.1, 0.75, 0, 0, 0, 0, 0, 0.05]，这表示当前图片有10%的概率是1， 10%的概率是2，75%的概率是3， 5%的概率是9（PS：当然有很多方法表示结果，我只是用了最简单的方式）。全连接层工作的方式就是查看前一层的输出结果（高级特征的活动图）然后判断哪一个特征与特定的类别联系最多。例如，如果一个程序用于预测出一些图片是小狗，那么在代表类似于爪子和四条腿等高级特征的活动图中又有较大值。同样，如果如果程序预测一些图片是鸟，那么它应该在代表这翅膀或者鸟喙等高级特征的活动图中拥有较高的数值。由上可得，一个FC层寻找符合的特定类别的高层特征值和拥有的特定权重值，当你计算出权重和相应特征值的积时，你就得到了不同类别的判别概率。

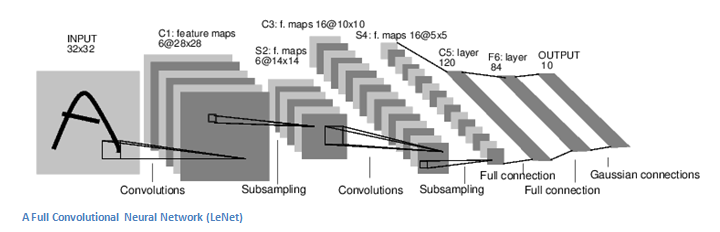
训练 （让特定网络工作的基础）

接下来就是我之前没有提到的也是最重要的一部分。阅读的过程中一定有很多问题吧。第一个conv层的过滤器怎么寻找直线和曲线呢？完全连接层又怎么知道要察看哪一张活动图呢？每一层的过滤器怎么知道应该选取哪一个值？计算机敲定过滤器的值的方法是一个叫做前馈反传(backpropagation)的训练过程。

在我们了解前馈反传之前，我们首先需要做的是了解一下如果要神经网络需要些什么才能起作用。我们出生的那一刻，我们的大脑还很纯净。我们并不知道什么是猫什么是狗哪个又是鸟。同样的，在CNN启动之前，权重或者是过滤器的值是随机的，过滤器并不知道要寻找直线和曲线，高层次的过滤器也不知道要寻找爪子和鸟喙。当我们逐渐长大，我们的父母和老师向我们展示不同的图片并告诉我们图片中的是什么。这个给出图片和相应标签的过程就是CNN的训练过程。在深入了解之前，我们假装现在有一个训练集，里面是上千张的包含了狗，猫和鸟的图片，并且每一张图片也有对应标签标明图片中的是哪种动物。

前馈反传分为四个部分。前馈(forward pass)，损失函数(loss function)，反馈(backward function)和权重更新(weight update)。在前馈部分，你要把训练集里的一个图片（就是那个 $32 \times 32 \times 3$ 的数组）扔进网络中。对于第一个被扔进去的例子，由于一开始的权重是随机的，输出有可能会是像[0.1, 0.1, 0.1, 0.1, 0.1, 0.1 ,0.1 ,0.1, 0.1, 0.1]这样的——不偏向任何一个特定的数字。拥有当亲权重的这个网络，并不能找到低层次的特征同时也不能对分类给出一个有用的结论。然后就到了前馈反传的损失函数部分。我们现在使用的是训练数据。这个数据不但有图片还有标签。我们假设第一个被扔进去的例子的标签是3，那对应这幅图片的标签就是[0, 0, 1, 0, 0, 0, 0, 0, 0, 0]。损失函数有许多定义的方法其中最常用的是MSE(平均平方误差, mean squared error)，是指（实际值 - 预测值）平方的一半。

我们假设变量L代表这个值。如你所想，对于前两组训练图片来说损失函数的值会非常大。而我们的目的是为了让预测值（网络的输出结果）和训练数据本身的标签值相同（也就是说网络的预测结果是正确的）。为了获得那个效果，我们要做的是降低损失函数的和值。这个问题可以被具象化为微积分的优化问题。我们要找出哪一个输入（权重）引起了网络的损失（或者错误）。

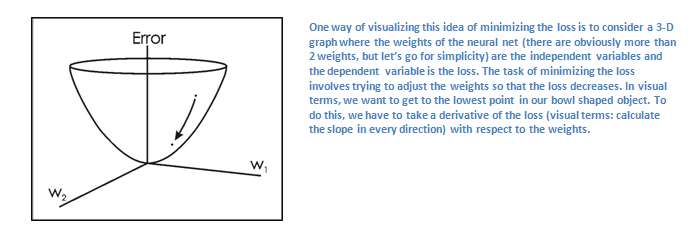
下面是一个关于dL/dW的数学等式，其中W表示特定层的权重。现在我们要做的是在网络中执行一次反馈(backward pass)，即判断出那一部分权重对造成的损失最多并且找到一些方法调整使得损失降低。如果我们计算出导数，我们就可以进行最后一个部分权重更新了。这才是我们要处理并更新过滤器权重的部分以使得它们可以向梯度的反方向变化。

学习度(learning rate)是程序选择的一个参数。较高的学习度意味着在权重更新时可以大幅度改变它们的值，从而可以在更少的时间里让模型跑到最佳的权重集合上。另一方方面，高学习度也会导致结果跳跃的幅度过大从而不能精确地达到最有解。

前馈，损失函数计算，反馈和参数更新算一次训练迭代。对于每一个训练集的图片（通常都称为一批）这个程序都会重复这个过程以进行固定次数的迭代。当你完成最后一个训练集的参数更新部分时，这个网络也许已经足够训练得非常好了即所有层的参数都变得正确了。

测试

最后，为了检验我们的CNN是否真的可以工作，我们有一个不同的图像和标签的集合（和测试集完全不同的）然后将这些图片扔进CNN网络。我们可以通过对比输出和真实值判断我们的网络是否真的起作用了。

CNN是怎样运用到工作中的

数据！数据！数据!哪些拥有大量这两个字会在接下来的竞争中拥有绝对优势。你给网络的训练数据越多，你能进行的迭代此时就越多，也就能进行更多次数的权重更新，然后就能在生产创造中就能得到更好的产出汇报。Facebook(和 Instagram)可以使用它现在拥有的数十亿的用户图片，Pinterest 也可以用它站点上的500亿的图片信息，Google可以用搜索数据，Amazon可以使用从每天购买的数百万商品中获取的数据。那么现在你知道它们如何使用这个魔法了。

最后的PS

也许这篇文章对于理解CNN是一个很好的开始，但并不是一个全面的概述。这篇文章没有提及到的包括非线性和池化层(nonlinear and pooling layer)和网络的超参数(hyperparameters)，例如过滤器的大小，步进和填充。像网络结构(network architecture)、批处理标准化(batch normalization)、梯度消失(vanishing gradients)，dropout，初始化方法(initialization techniques)，非凸优化(non-convex optimization)、偏差(biases)、损失函数的选择(choices of loss functions)、数据展开(data argumentation)、标准化方法(regularization methods)、计算方法(computational considerations)、反向传播的修改(modifications of backpropagation)等话题以及其他很多很多的东西都没有讨论到（至少暂时没有）。