模型评估

信用评分

---

这里介绍对模型进行评估的方法和指标。
通过，一个logisitc回归只有达到三项基本要求才可以被看作建立评分卡的好的备选。

1. 精确性。在预测状态变量时，模型必须具有一定的精确性。
2. 稳健性。模型必须对从目标总体中抽取的所有样本都有效。
3. 有意义。模型表现出来的趋势对于预测到的行为必须具有意义。
   除了上述模型的要求，模型开发人员更倾向于开发所谓的简约模型。
   这里先介绍模型验证和验证数据集的使用；其次将探索并介绍几个准确性指标的SAS实施；最后将讨论总体模型的验证。

验证和混淆矩阵

用检验数据集运行模型被称为交叉验证。验证结果就是计算已知违约结果的预测概率。
选择检验数据集的方法很简答。通常，用随机抽样从违约状态已知的总体中抽取检验数据集。
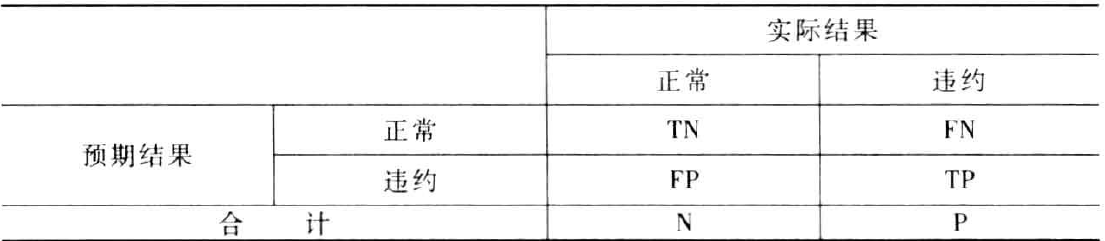
接下来，将假设为建立评分卡而开发的logistic回归模型将对违约的概率进行预测，如果预测概率大于0.5，则将被认定为违约，将这些数值整理放入一个矩阵，如下表：

其中，

• TN: True Negative，分类准确的正常记录数
• TP: True Positive，分类准确的违约记录数
• FN: False Negative，分类错误的违约记录数
• FP: False Positive，分类错误的正常记录数

下图显示的是开发数据集分段的估计概率的频率分布。

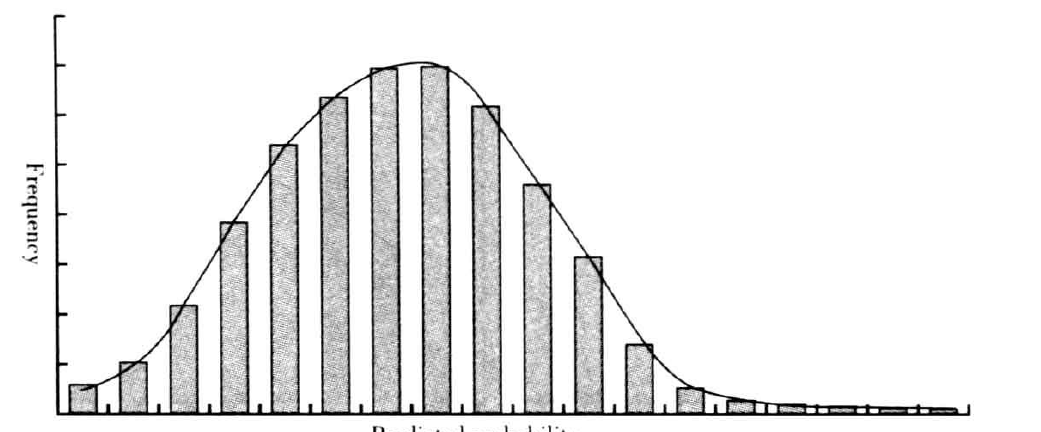
下图显示正常和违约样本以及整个开发数据集的预测概率的频率分布。

垂直的虚线代表当前的临界值。上图表明，混淆矩阵中的要素就是正常和违约记录的频率分布之下的区域。

宏%ConfMat用包含估计概率的数据集Pred_Probs来计算混淆矩阵，其中临界值设定为0.50。宏的参数如下：

下列程序用来计算混淆矩阵：

%let VarList=CustAge_WOE   TmAtAddress_WOE CustIncome_WOE 
             TmWBank_WOE   AmBalance_WOE   UtilRate_WOE    
             ResStatus_WOE EmpStatus_WOE   OtherCC_WOE;
proc logistic data=cc.CC_WOE OUTEST=cc.Model_Params;
model Status (event='1')=&VarList / selection =stepwise  sls=0.05 sle=0.05;
OUTPUT OUT=cc.Pred_Probs    P=Pred_Status;
run;
%let DSin=cc.Pred_Probs; /* predicted probabilities*/
%let DVVar=status;
%let ProbVar=Pred_Status;
%let Cutoff=0.5;
%let DSCM=ConfusionMatrix;
%ConfMat(&DSin, &ProbVar, &DVVar, &Cutoff, &DSCM);

计算出的混淆矩阵的条目：

得到混淆矩阵：

提升图和洛沦兹曲线

提升图主要通过随机选择比较模型表现。例如，如果已知特定总体的预期违约率，有理由由预期占总体10%的随机样本，即客户总体的十分之一将包含违约总量的10%。然而，如果选择的十分之一根据模型计算的预期违约率最高，则可以预期其中违约的样本量超过总体违约量的10%。按照总体的十分之一画出这两个值就是提升图，也被称为洛沦兹曲线或收益曲线。

例如，用一个总量为10000，违约率为7%，即违约记录为700个的样本对模型进行拟合。建立logistic回归模型后，对10000个记录进行评分并计算估计的违约概率。将这些记录按照概率的降序排列并分为10等分，如下表所示：

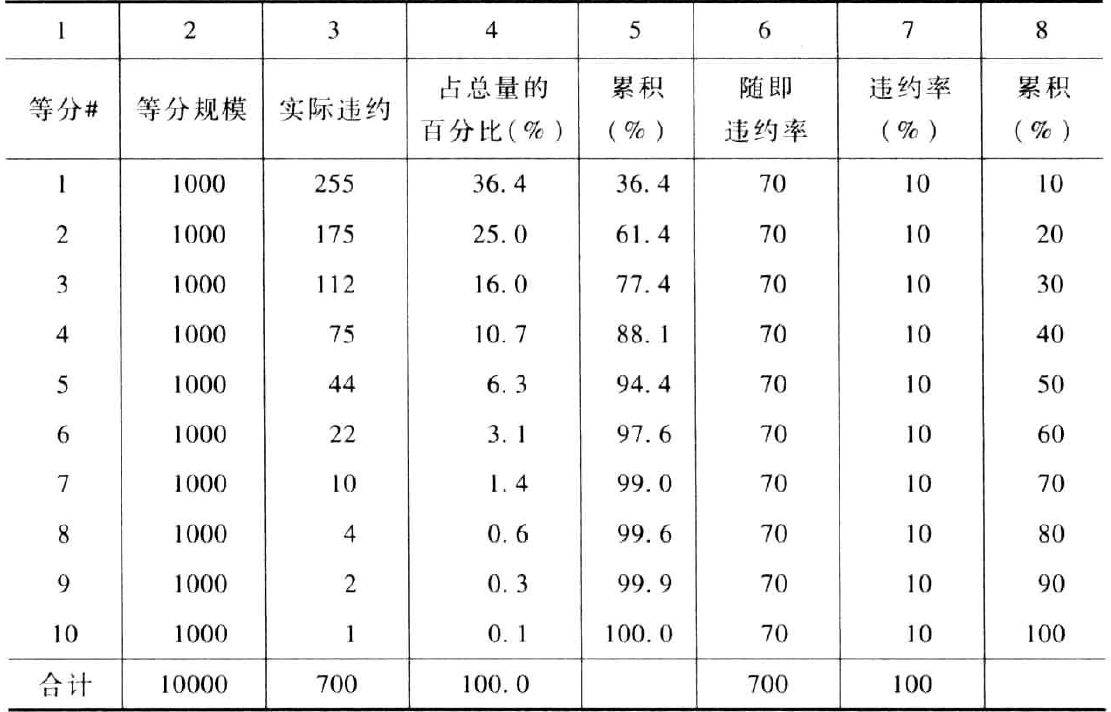
第三列表示按照违约概率降序排列的每个10等份中的实际违约数。
第四列表示这些违约数占违约总量的比例。
第五列是违约数占违约总量百分比的累积值，即洛沦兹曲线。

但是，对第1到10等分的记录是随机选择的情况，第6、7、8列的计算方法与第3、4、5列相同。这种情况下，预期每一等分有相同数量的违约数量，即违约总量的10%。下图表示该数据的提升图和洛沦兹曲线：

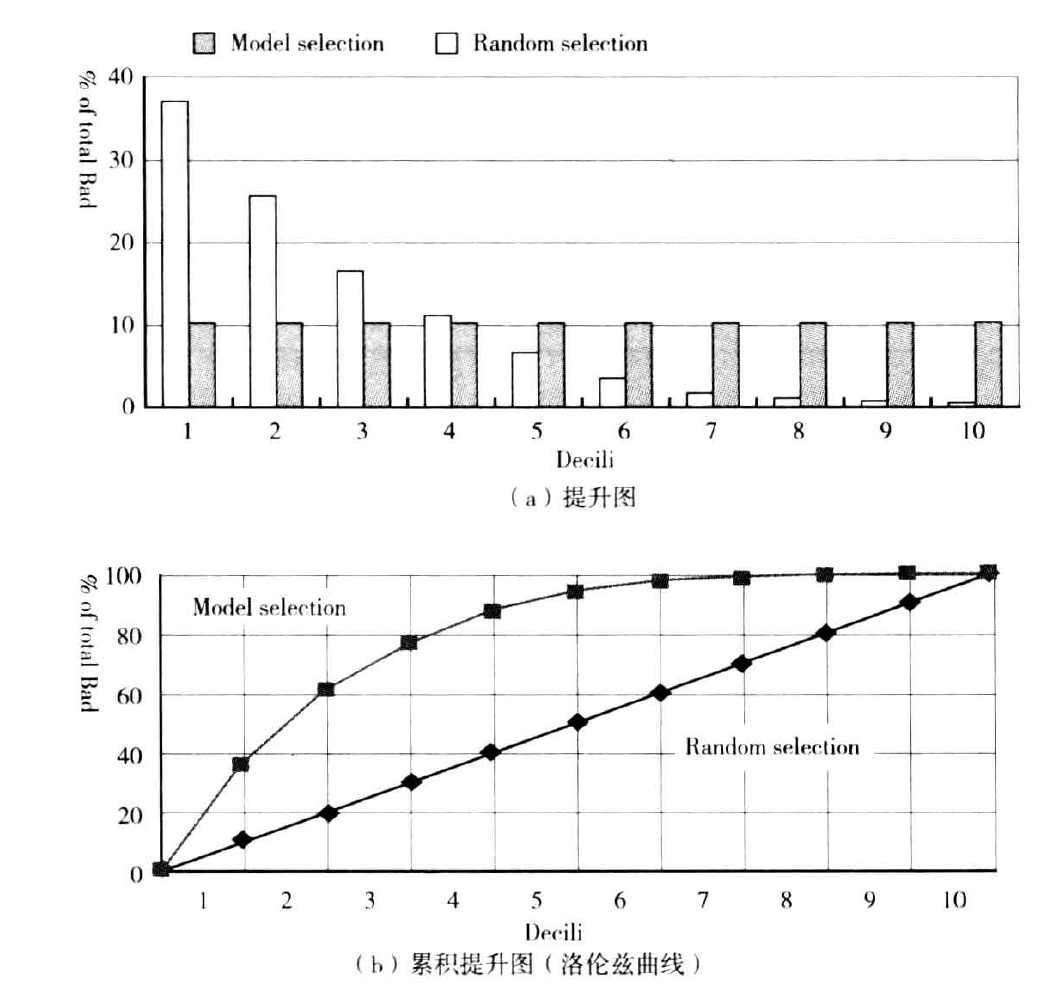
在申请评分卡的情况下，累计提升图可以解释为横轴是被拒绝申请的百分比。如果组织目标是一个特定的审批通过率，则可以用该特定值的洛沦兹曲线对模型进行比较。
下图表示预期审批通过率为60%的两个模型，这意味着拒绝率为40%，如图中虚线所示。模型A预计将识别94%的违约账户，而模型B只能识别79的违约账户。

除了比较模型表现与随机选择的差别，提升图还可以识别任何隐藏的模型问题。例如下图。

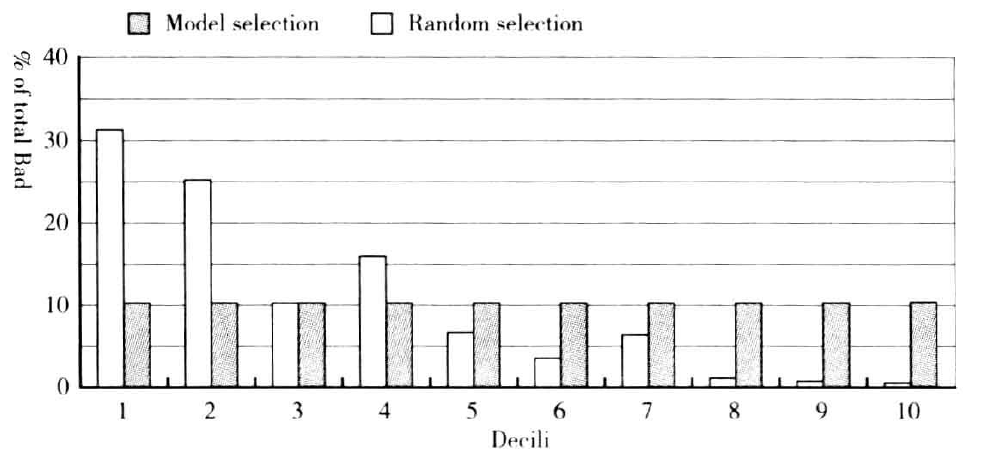
该图表明，每一等分长的违约模式并不是单调递减。第三等份中的违约数下降，而第四等份中的违约数又再次上升，第七等份也表现出同样的行为。一旦发生这种概率不一致，该模型就被认为是不可用的，需要开发新的模型。

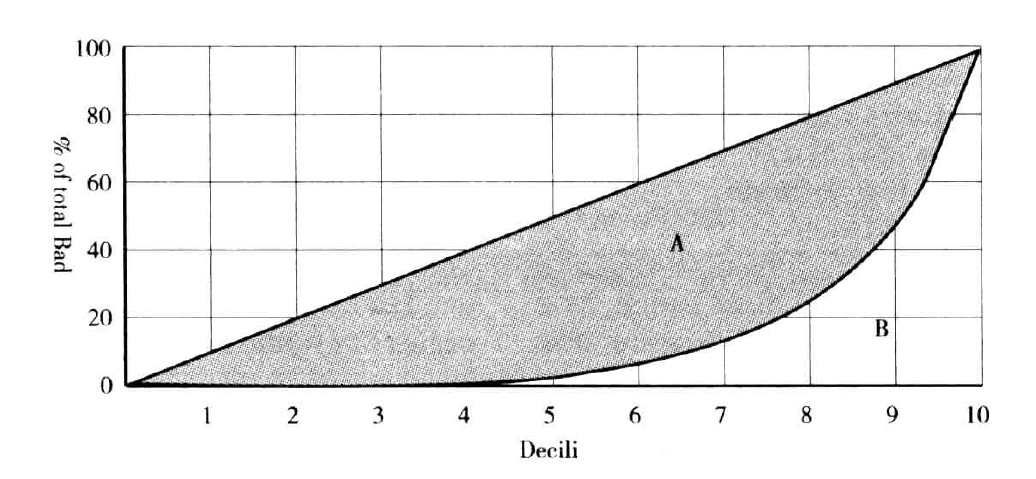
基尼系数

考虑之前的洛沦兹曲线。这里的洛沦兹曲线是总体的10等分按照违约概率的升序排列而绘制的。这种情况下，基尼系数，或基尼统计量，定义为：

$$G = \frac{A}{A+B} = 24$$
其中，A和B分布代表下图中的相应区域。G的值在0到1之间。在随机选择的情况下，G取0；最优分类模型情况下，G取1。

根据洛沦兹曲线的数据计算基尼统计量的一种简单的方法是使用梯形逼近法则。在这种情况下，用一系列的直线逼近曲线，而曲线下的区域可以通过简单的求和计算。可用宏%GiniStat实现这以策略，其参数如下：

示例如下：

%let VarList=CustAge_WOE   TmAtAddress_WOE CustIncome_WOE 
             TmWBank_WOE   AmBalance_WOE   UtilRate_WOE    
             ResStatus_WOE EmpStatus_WOE   OtherCC_WOE;
proc logistic data=cc.CC_WOE OUTEST=cc.Model_Params;
model Status (event='1')=&VarList / selection =stepwise  sls=0.05 sle=0.05;
OUTPUT OUT=cc.Pred_Probs    P=Pred_Status;
run;
/* Calculate the Gini statistic */
%let DSin=cc.Pred_Probs;
%let ProbVar=Pred_Status;
%let DVVar=Status;
%let DSLorenz=LorenzDS;
%let Gini=;
%GiniStat(&DSin, &ProbVar, &DVVar, &DSLorenz, Gini);
%put>>>>>>>>>>>>>>>   Gini=&Gini  <<<<<<<<<<<<<<<<<<<  ;

输出：

K-S曲线和统计量

与洛沦兹曲线密切相关的是柯尔莫戈洛夫-斯米尔诺曲线，简称K-S曲线。将总体进行10等分并按照违约概率的降序排序，计算每一等份中违约与正常百分比的累积分布，绘制出两者之间的差异，就得到K-S曲线。如下图：

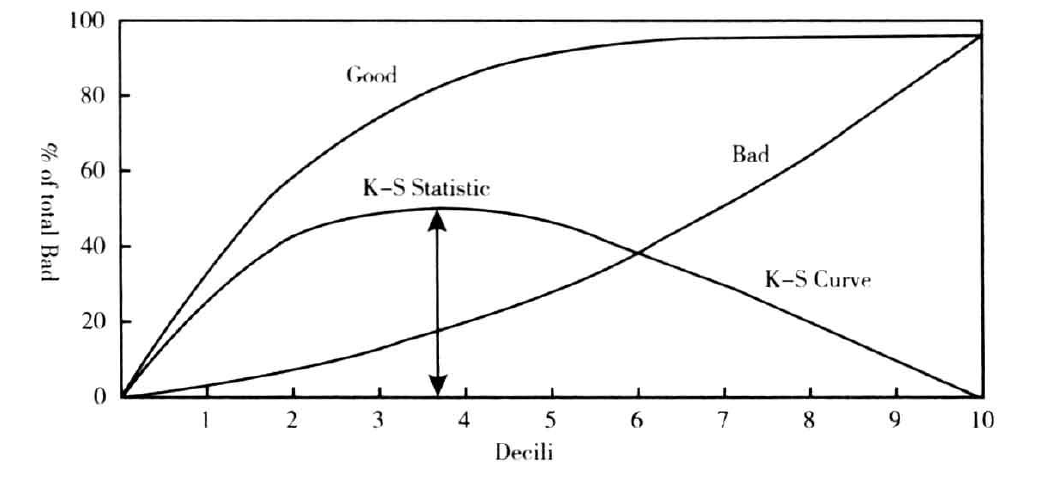
K-S曲线中的最大值被称为K-S统计量，其取值在0到1之间。采用随机抽样时，K-S统计量的值为0；当最优分类时，K-S统计量的值为1。宏%KSStat的可以计算K-S值，其参数如下表：

ROC曲线和c-统计量

给出下列混淆矩阵的定义：

• 灵敏度（sensitivity）是真实的正值与总的正值的比例。 $$sensitivit\frac{TP}{P}=\frac{TP}{TP+FN}$$
• 特异度（specificity）是真实负值与总的负值的比例。 $$specificity = \frac{TN}{N}=\frac{TN}{TN+FP}$$
• 分类错误的正常记录比例（false positive rate, FPR）是： $$FPR=\frac{FP}{N}=\frac{FP}{TN+FP}=1-specificity$$
  受试者工作特征曲线（ROC）是通过在0到1之间改变用于创建混淆矩阵的临界值，绘制分类灵敏度与1-特异度而得到的，如下图所示：
  
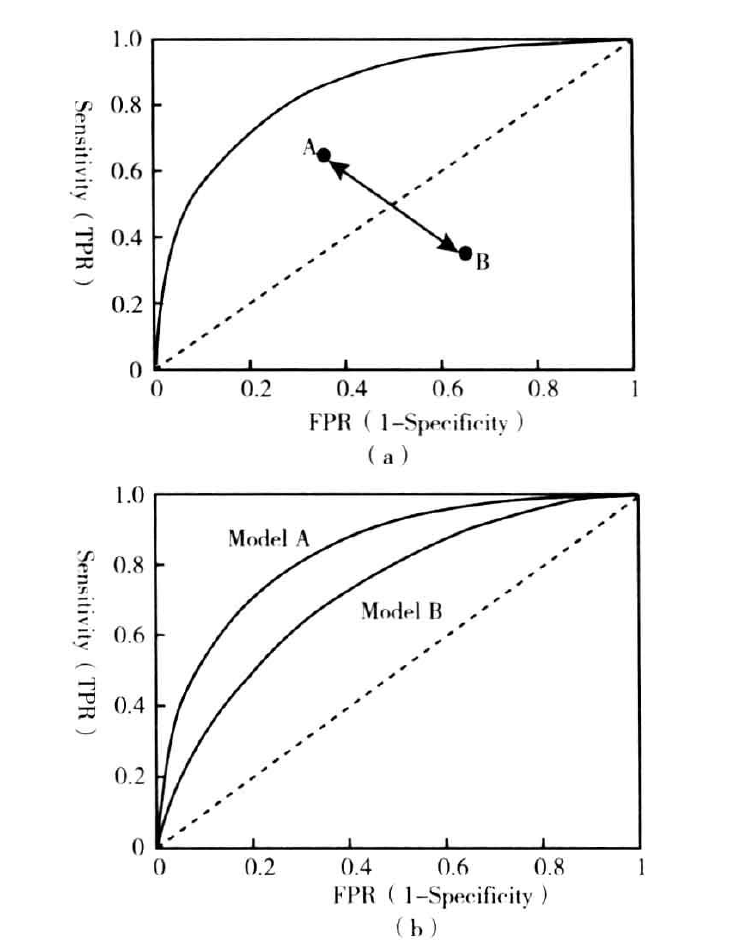
  鉴于ROC曲线的定义，对角线以上的图形越高，模型就越好。上图中，模型A的表现优于模型B。
  ROC曲线之下的面积被称为AUC或C-统计量。当前，信用评分行业的最优实践建议C-统计量大于或等于0.75时，建立的行为评分卡是可靠的。C-统计量和基尼统计量之间存在一下的简单关系：
  $$c = \frac{1}{2}(G+1)$$
  因此，0.75的C-统计量等价于0.50的基尼统计量。
  proc logistic的标题为Association of Predicted Probabilities and Observed Response的结果部分输出c统计量的值。而且，ROC曲线的数据也可以在model语句中用选项outroc=dataset生成。该选择创建一个包含ROC曲线坐标的数据集，用该数据集也可以计算出C-统计量。
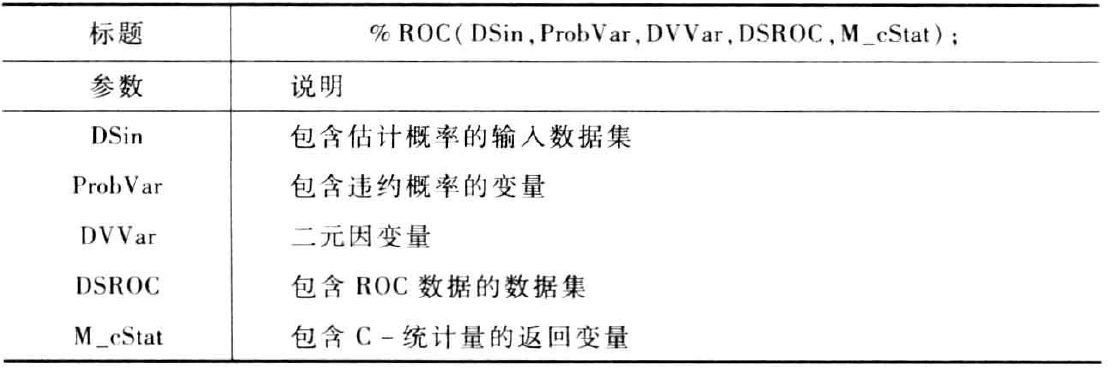
  宏%ROC可以计算ROC图的数据及相关的C-统计量。它允许计算其他数据集的C-统计量，而不仅仅是logistic生成的建模数据。其参数如下：
  

整体模型评估

一个好的模型一般应具有以下特征：

1. 在进行数据描述时变量应该有意义。通常，某些变量在特定申请人的不同风险模型中重复出现。
2. 变量的预测力，用概率比衡量，应该在模型中使用的变量之间的分布。没有一个变量能够主导模型。如果发生这种情况，会生成一个较弱的评分卡和实施阶段的高误差率。
3. 模型中不应该包含太多变量。通常，模型中包含不超过10-12个变量。使用太多变量开发的模型通常是由这些变量中一个很小的子集主导，而包含太少变量的模型往往不够稳健。
4. 用于最终模型的变量应该能够确保包含稳健和一致的数据，并在实施阶段能够准确获得。一些变量尽管表现出很强的预测力，但却无法获得。
5. 需要根据实施阶段获取征信机构评分的预期成本判断外部征信机构数据对最终模型的贡献度。而且，模型不应该完全或几乎完全依赖征信机构评分。