学习机器学习之如何根据需求选择一种算法

随着机器学习的进一步火热，越来越多的算法已经可以用在许多任务的执行上，并且表现出色。

但是动手之前到底哪个算法可以解决我们特定的实际问题并且运行效果良好，这个答案很多新手是不知道的。如果你处理问题时间可以很长，你可以逐个调研并且尝试它们，反之则要在最短的时间内解决技术调研任务。

Michael Beyeler的一篇文章告诉我们整个技术选型过程，一步接着一步，依靠已知的技术，从模型选择到超参数调整。

在Michael的文章里，他将技术选型分为6步，从第0步到第5步，事实上只有5步，第0步属于技术选型预积累步骤。

第0步：了解基本知识

在我们深入之前，我们要明确我们了解了基础知识。具体来说，我们应该知道有三个主要的机器学习分类：监督学习（supervised learning）、无监督学习（unsupervised learning），以及强化学习（reinforcement learning）。

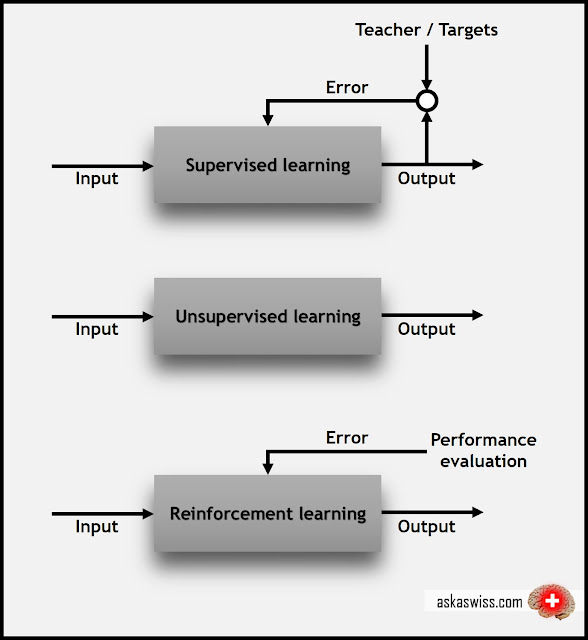
• 监督学习：每个数据点被标记或者与一个类别或者感兴趣值相关联。分类标签的一个例子是将图像指定为“猫”或者“狗”。价值标签的一个例子是销售价格与二手车相关联。监督学习的目标是研究许多这样的标记示例，进而能够堆未来的数据点进行预测，例如，确定新的照片与正确的动物（分类（classification））或者指定其他二手车的准确销售价格（回归（regression））。

• 无监督学习：数据点没有标签对应。相反，一个无监督学习算法的目标是以一些方式组织数据或者表述它的结构。这意味着将其分组到集群内部，或者寻找不同的方式查看复杂数据，使其看起来更简单。

• 强化学习：对应于每一个数据点，算法需要去选择一个动作。这是一种常见的机器人方法，在一个时间点的传感器读数集合是一个数据点，算法必须选择机器人的下一个动作。这也是很普通的物联网应用模式，学习算法接收一个回报信号后不久，反馈这个决定到底好不好。基于此，算法修改其策略为了达到更高的回报。

第1步：对问题进行分类

下一步，我们要对手头上的问题进行分类。这是一个两步步骤：

• 通过输入分类：如果我们有标签数据，这是一个监督学习问题。如果我们有无标签数据并且想要去发现结构，这是一个无监督学习问题。如果我们想要通过与环境交互优化目标函数，这是一个强化学习问题。

• 通过输出分类：如果一个模型的输出是一个数字，这是一个回归问题。如果模型的输出是一个类（或者分类），这是一个分类问题。如果模型的输出是输入组的集合，这是一个分类问题。

就是那么简单。总而言之，我们可以通过问自己算法需要解决什么问题，进而发现算法的正确分类。

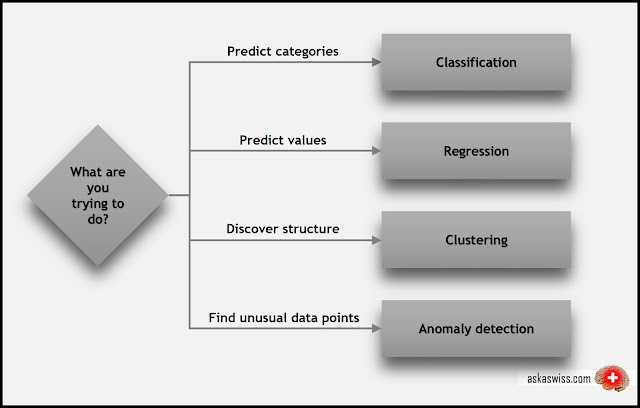
上面这张图包含了一些我们还没有讨论的技术术语：

• 分类（Classification）：当数据被用来预测一个分类，监督学习也被称为分类。这是一个例子当指定一张相作为“猫”或“狗”的图片。当只有两种选择时，称为二类（two-class）或二项式分类（binomial
  classification）。当有更多类别的时候，当我们预测下一个诺贝尔物理学奖得住，这个问题被称为多项式分类（multi-class
  classification）。

• 回归（Regression）：当一个值被预测时，与股票价格一样，监督学习也被称为回归。

• 聚类（Clustering）：非监督学习最常用的方法是聚类分析或者聚类。聚类是一组对象组的任务，在这样的一种方式下，在同一组中的对象（称为集群）是更加相似的（在某一种意义上），相比其他组（集群）里的对象。

• 异常检测（Anomaly
  detection）：需要在目标里找到不寻常的数据点。在欺诈检测里，例如，任何非常不寻常的信用卡消费模式都是可以的。可能的变化很多，而训练示例很少，这看起来不是一种可行方式了解欺诈活动。异常检测需要的方法是简单地了解什么是正常的活动（使用非欺诈交易历史记录），并且确定明显不同的内容。

第2步：找到可用的算法

现在我们有分类问题，我们可以使用工具去调研和验证算法是可行的和可实践的。

Microsoft Azure已经创建了一个方便的算法表格，这个表格显示算法可以被用于哪些问题分类。虽然这个表格是针对Azure软件，它一般适用于：

一些值得关注的算法是：

分类（Classification）：

• 支持向量机（SVM）：通过尽可能宽的边缘方式发现分离类的边界。当二分式不能清晰的切分时，算法找到最好的边界。这个算法真正的亮点是强烈的数据特征，好像文本或者染色体组（>100特性）。在这些情况下，SVMs比其许多其他算法更快递切分二项，也更少地过度拟合，除了需要少量的内存。

• 人工神经网络（Artificial neural networks）：是大脑启发学习算法，覆盖多项式分类、二项式分类，以及回归问题。它们带来了无限的多样性，包括感知和深度学习。它们花费很长时间进行训练，但是带来各种应用领域的先进性能。

• 逻辑回归（Logistic regression）：虽然包含‘回归’这个词看上去有点令人费解，逻辑回归事实上是一个对于二项式和多项式分类来说强大的功能。它很快和简单。事实是它使用了‘S’形曲线代替直线让它对于切分数据进入组变得很自然。逻辑回归给出线性分类边界（linear class boundaries），所以当你使用它来确保一个线性近似的时候，类似于你生活中可以使用的一些东西。

• 决策树和随机树（Decision trees、random forests）：决策森林（回归、二项式，以及多项式），决策丛林（二项式、多项式），以及提高决策树（回归和二项式）所有被称为决策树，一种机器学习的基本概念。决策树的变种有很多，但是它们都做了相同的事情，使用相同的标签细分特征空间到各个区域。这些可以是一致类别或者恒定值的区域，依赖于是否你正在做分类或者回归。

回归（Regression）：

• 线性回归（Linear
  regression）：线性回归拟合直接（或者平台，或者超平面）数据集。这是一个工具，简单而快速，但是对于一些问题可能过于简单。

• 贝叶斯线性回归（Bayesian linear
  regression）：它有非常可取的品质，避免了过度拟合。贝叶斯方式实现它通过对可能分布的答案作出一些假设。这种方式的其他副产品是它们有很少的参数。

• 提高决策树回归：如上所述，提高决策树（回归或二项式）是基于决策树的，并通过细分大多数相同标签的特征空间到区域完成。提高决策树通过限制它们可以细分的次数和每一个区域的最小数据点数量避免过度拟合。算法构造一颗序列树，每一颗树学习补偿树前留下的错误。结果是非常准确的学习者，该算法倾向于使用大量内存。

聚合（Clustering）：

• 层次聚类（Hierarchical
  clustering）：层次聚类的试图简历一个层次结构的聚类，它有两种格式。聚集聚类（Agglomerative
  clustering）是一个“自下而上”的过程，其中每个观察从自己的聚类开始，随着其在层次中向上移动，成对的聚类会进行融合。分裂聚类（Divisive
  clustering）则是一种“自顶向下”的方式，所有的观察开始于一个聚类，并且会随着向下的层次移动而递归式地分裂。整体而言，这里进行的融合和分裂是以一种激进的方式确定。层次聚类的结果通常表示成树状图（dendrogram）形式。

• k-均值聚类（k-means
  clustering）的目标是将n组观测值分为k个聚类，其中每个观测值都属于其接近的那个均值的聚类，这些均值被用作这些聚类的原型。这会将数据空间分割成Voronoidan单元。

异常检测（Anomaly detection）：

• K最近邻（k-nearest
  neighbors/k-NN）是用于分类和回归的非参数方法。在这两种情况下，输入都是由特征空间中与k最接近的训练样本组成的。在k-NN分类中，输出是一个类成员。对象通过其k最近邻的多数投票来分类，其中对象被分配给k最近邻并且最常见的类（k是一个正整数，通常较小）。在k-NN回归中，输出为对象的属性值。该值为其k最近邻值的平均值。

• 单类支持向量机（One-class
  SVM）：使用了非线性支持向量机的一个巧妙的扩展，单类支持向量机可以描绘一个严格概述整个数据集的边界。远在边界之外的任何新数据点都是足够非正常的，也是值得特别关注的。

第3步：实现所有适用的算法

对于给定的问题，通常会有一些候选算法可以适用。所以我们如何知道哪一个可以挑选？通常，这个问题的答案不是那么直截了当的，所以我们必须反复试验。

原型开发最好分两步完成。第一步，我们希望通过最小化特征工程快速而简单地完成几种算法的实现。在这个阶段，我们主要兴趣在粗略来看那个算法表现更好。这个步骤有点类似招聘：我们会尽可能地寻找可以缩短我们候选算法列表的理由。

一旦我们将列表缩减为几个候选算法，真正的原型开发开始了。理想地，我们想建立一个机器学习流程，使用一组经过精心挑选的评估标准比较每个算法在数据集上的表现。在这个阶段，我们只处理一小部分的算法，所以我们可以把注意力转到真正神奇的地方：特征工程。

第4步：特征工程

或许比选择算法更重要的是正确选择表示数据的特征。从上面的列表中选择合适的算法是相对简单直接的，然而特征工程却更像是一门艺术。

主要问题在于我们试图分类的数据在特征空间的描述极少。利如，用像素的灰度值来预测图片通常是不佳的选择；相反，我们需要找到能提高信噪比的数据变换。如果没有这些数据转换，我们的任务可能无法解决。利如，在方向梯度直方图（HOG）出现之前，复杂的视觉任务（像行人检测或面部检测）都是很难做到的。

虽然大多数特征的有效性需要靠实验来评估，但是了解常见的选取数据特征的方法是很有帮助的。这里有几个较好的方法：

• 主成分分析（Principal component
  analysis，PCA）：一种线性降维方法，可以找出包含信息量较高的特征主成分，可以解释数据中的大多数方差。

• 尺度不变特征变换（Scale-invariant feature
  transform，SIFT）：计算机视觉领域中的算法，用以检测和描述图片的局部特征。它有一个开源的替代方法
  ORB（Oriented FAST and rotated BRIEF）。

• 加速稳健特征（Speeded up robust features，SURF）：SIFT 的更稳健版本。

• 方向梯度直方图（Histogram of oriented
  gradients，HOG）：一种特征描述方法，在计算机视觉中用于计数一张图像中局部部分的梯度方向的发生。

• 更多算法请参考：https://en.wikipedia.org/wiki/Visual_deor

当然，你也可以想出你自己的特征描述方法。如果你有几个候选方法，你可以使用封装好的方法进行智能的特征选择。
前向搜索：

• 最开始不选取任何特征。

• 然后选择最相关的特征，将这个特征加入到已有特征；计算模型的交叉验证误差，重复选取其它所有候选特征；最后，选取能使你交叉验证误差最小特征，并放入已选择的特征之中。

• 重复，直到达到期望数量的特征为止！

反向搜索：

• 从所有特征开始。
• 先移除最不相关的特征，然后计算模型的交叉验证误差；对其它所有候选特征，重复这一过程；最后，移除使交叉验证误差最大的候选特征。
• 重复，直到达到期望数量的特征为止！

使用交叉验证的准则来移除和增加特征！

第5步：超参数优化（可选）

最后，你可能想优化算法的超参数。例如，主成分分析中的主成分个数，k 近邻算法的参数 k，或者是神经网络中的层数和学习速率。最好的方法是使用交叉验证来选择。

一旦你运用了上述所有方法，你将有很好的机会创造出强大的机器学习系统。但是，你可能也猜到了，成败在于细节，你可能不得不反复实验，最后才能走向成功。

相关知识

二项式分类（binomial classification）：

适用环境：　

1．各观察单位只能具有相互对立的一种结果，如阳性或阴性，生存或死亡等，属于两分类资料。
2．已知发生某一结果（阳性）的概率为p，其对立结果的概率为1−p，实际工作中要求p是从大量观察中获得比较稳定的数值。
3．n次试验在相同条件下进行，且各个观察单位的观察结果相互独立，即每个观察单位的观察结果不会影响到其他观察单位的结果。如要求疾病无传染性、无家族性等。

符号：b(x,n,p)
概率函数*：Cxnpxqn−x，其中x=0,1,⋯,n为正整数即发生的次数，Cxn=n!x!(n−x)!

例题：
掷硬币试验。有10个硬币掷一次，或1个硬币掷十次。问五次正面向上的概率是多少?

解：根据题意n＝10，p＝q＝12，x＝5
　　b(5,l0,12)=C510p5q10=10!(5!(10−5)!)×(12)5×(12)5=252×(132)×(132)=0.2469
所以五次正面向上的概率为0．24609

Support vector machines

是一种监督式学习的方法，可广泛地应用于统计分类以及回归分析。支持向量机属于一般化线性分类器，也可以被认为是提克洛夫规范化（Tikhonov Regularization）方法的一个特例。这族分类器的特点是他们能够同时最小化经验误差与最大化几何边缘区，因此支持向量机也被称为最大边缘区分类器。

全文总结

所有的技术选型原理都是类似的，首先需要你的自身知识积累，然后是明确需要解决的问题，即明确需求。接下来确定一个较大的调研范围，进而进一步调研后缩小范围，最后通过实际应用场景的测试挑选出合适的技术方案或者方法。机器学习算法选择，也不例外。

参考文献主要作者介绍

Michael Beyeler：Moore/­Sloan/­WRF创新公司联合创始人、华盛顿大学生物信息学研究员，主攻仿生视觉计算理论模型，研究目标是提高视网膜假体植入患者的知觉体验。著有《OpenCV with Python Blueprints》一书，该书使用OpenCV和Python开发高级计算机视觉项目。