Ising Model

　物基一班　张志城　2013301110121

Contents

Abstract

　　In this passage,I calculate some thermodynamics quantities such as mean energy $E$, specific heat capacity $C$,and correlation function $G(r)$ of one-dimensional Ising model,and I compare them with analytical results acquired by Ernst Ising.Besides,I calculate mean energy $E$,magnetization $M$,specific heat capacity $C$ of two-dimensional Ising model and I verify that there exist pahse transitions in two-dimensional model.
　　

Background

Introduction of Ising Model

　　Magnetic systems such as the magnets are familiar to us in everyday life.The magnet likely consists of iron ions localized on sites of a lattice with conduction electrons that are free to move throughout the crystal.The iron ions each have a magnetic moment and they tend to line up with each other.Materials that retain a nonzero magnetization are called ferromagnetic.At high temperatures there is enough energy to the magnetization,and the iron is said to be in paramagnetic phase.
　　The absence of interactions between spins means that the system can only be paramagnetic.The most important and simplest system that exhibts transition from ferromagnetic phase to paramagnetic phase is Ising model.
　　Ising model was first proposed by Wilhelm Lenz in 1920 and solved exactly for one dimension by his student Ernst Ising in 1925.Lars Onsager solved the Ising model exactly in 1944 for two dimensions in the absence of external magnetic field and showed that there was a phase transition in two dimensions.
　　In the Ising model the spin at every site is either up or down. The interaction is between nearest neighbors only and is given by $-J$ if the spins are parallel and $+J$ if the spins are antiparallel. And the total energy can be expressed in the form
　　　　$E=-J\sum_{i,j=nn(i)}^{N}s_{i}s_{j}-H\sum_{i=1}^{N}s_{i}$　　(1)

One-dimensional Ising Model:The Ising Chain

　　In the absence of an external magnetic field it is more convenient to choose free boundary conditions when calculating the partition function $Z$ directly.The energy of the Ising chain in the absence of external magnetic field with free boundary conditions is given explicitly by
　　　　$E=-J\sum_{i=1}^{N-1}s_{i}s_{i+1}$　(2)
　　Then we can derive the partition function:
　　　　$Z_{N}=\sum_{s_{1}=\pm1 }\sum_{s_{2}=\pm1}\cdots \sum_{s_{N}=\pm1}e^{\beta Js_{1}\sum_{i=1}^{N-1}s_{i}s_{i +1}}$　(3)
Next we can calculate the thermodynamics quantities:
　　　　$F=-kTlnZ_{N}=-NkTln(2cosh\beta J)$　(4)
　　　　$E=-NJtanh\beta J$　(5)
　　　　$C=Nk(\beta J)^{2}(sech\beta J)^{2}$　(6)
　　We can get further insight into the properties of the Ising model by calculating the spin-spin correlation function $G(r)$ defined as
　　　　$G(r)=< s_{k}s_{k+r}> -<s_{k} > < s_{k+r}>$　(7)
And $G(r)$ can be calculated exactly for the Ising chain and is given by:
　　　　$G(r)=(tanh\beta J)^{r}$　(8)
　　

Two-dimensional Ising Model

　　The key difference between one and two dimensions is that in the former the existence of one domain wall allows the system to have regions of up and down spins whose size can be changed without any cost of energy.So on average the number of up and down spins is the same. In two dimensions the existence of one domain does not make the magnetization zero.The regions of down spins cannot grow at low temperature because their growth requires longer boundaries and hence more energy.
　　Onsager derived the exact solution of two-dimensional Ising model.The critical temperature is given by$^{[1]}$
　　　　$\frac{kT_{c}}{J}=\frac{2}{ln(1+\sqrt{2})}\approx2.269$　(9)
　　　　$E=-2NJtanh2\beta J-NJ\frac{sinh^{2}2\beta J-1}{sinh2\beta Jcosh2\beta J}[\frac{\pi}{2}K_{1}(\kappa)-1]$　(10)
　　　　$C\approx-Nk\frac{2}{\pi} (\frac{2J}{kT_{C}})^{2}ln\left | 1-kT_{C} \right |+constant$　(11)
　　And C.N. Yang in 1952$^{[2]}$ calculated the magnetization for magnetization is
　　　　$m(T)=(1-[sinh2\beta J]^{-4})^{1/8},T<T_{C}$
　　　　$m=0,T>T_{C}$　(12)

The Metropolis Monte Carlo Algorithm

　　The Monte Carlo method is a powerful and quantitatively accurate picture of phase transition.It uses a stochastic approach to simulate the exhange of energy between the spin system and the heat bath. Following are the procedures of the algorithm$^{[3]}$.
　　A spin is chosen and the energy required to make it flip,$E_{flip}$,is calculated.If $E_{flip}$ is negative,then the spin is flipped and the system moves into a different microstate.If $E_{flip}$ is positive,a decision must be made.A random number that is uniformly distributed between 0 and 1 is generated,and compared to the Boltzmann factor $exp(\frac{-E_{flip}}{k_{B}T})$.If the Boltzmann factor is larger than the random number,the spin is flipped,otherwise the spin is left undisturbed.Then another spin is flipped,$E_{flip}$ is calculated,and the spin is determined to flip or not flip.This is called Metropolis algorithm.This procedure is repeated a large number of times so that every spin is given enough chances to flip.
　　

Source Codes

• 1D Ising model energy-temperature relation
• 1D Ising model specific heat capacity-temperature relation
• 1D Ising model correlation function-r relation
• 2D Ising model energy-temperature relation
• 2D Ising model specific heat capacity-temperature relation (differential method)
• 2D Ising model specific heat capacity-temperature relation (fluctuation-dissipation method)
• 2D Ising model magnetization-time relation
• 2D Ising model magnetization-temperature relation

Results

One-dimensional Ising Model

1、1D Ising model energy-temperature relation
　　　　
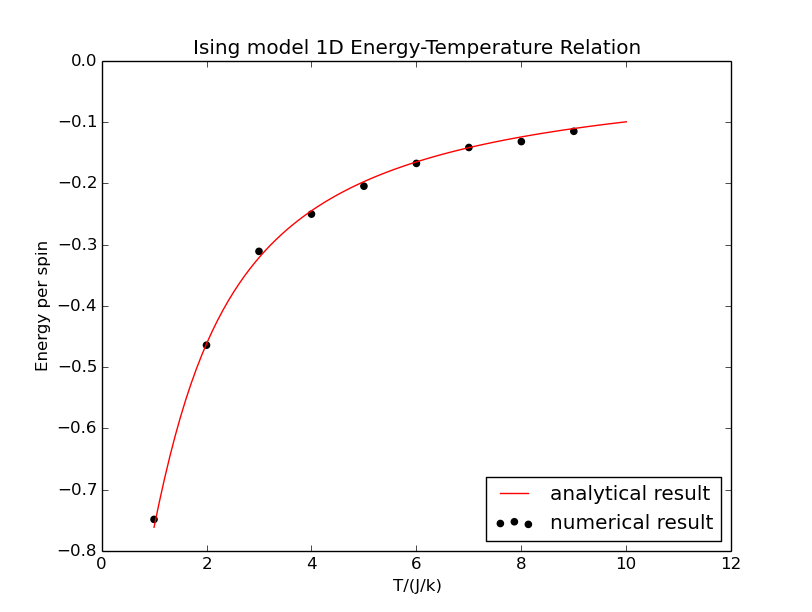
　　We can find that the result of Metropolis approach corresponds to the analytical result very well.It means that Metropolis approach is effective and powerful in solving Ising model.
2、1D Ising model specific heat capacity-temperature relation
　　　　
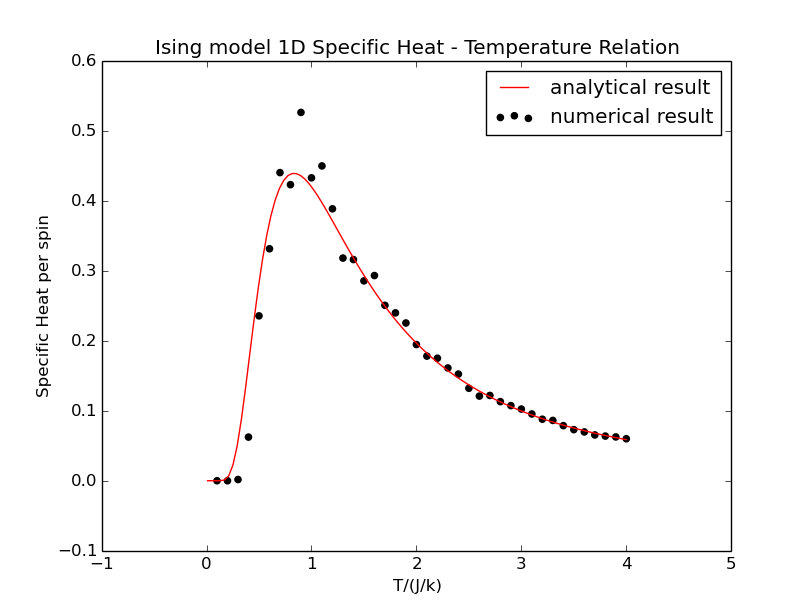
　　We can find that the result of Metropolis approach corresponds to the analytical result at most temperatures.For the temperatures near $T_{C}$ the fluctuation of energy and thus specific heat capacity is very significant,so the variance is a little great.
3、1D Ising model correlation function-r relation
　　　　
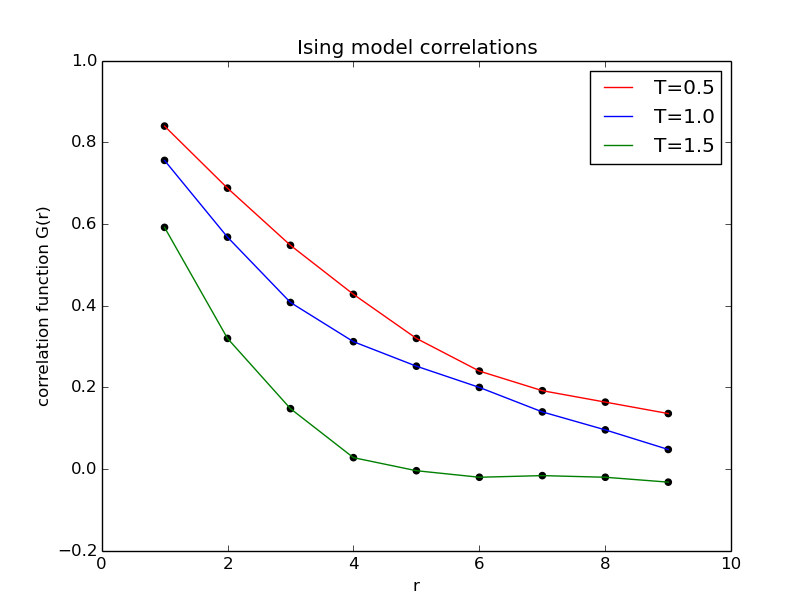
　　The result of Metropolis approach is reasonable.Because when $T$ is very small,all spins tend to point upward,$G(r)$ approaches to 1. Besides,with the increase of $r$,the interaction between two spins approaches to 0.

Two-dimensional Ising Model

4、2D Ising model energy-temperature relation
　　　　
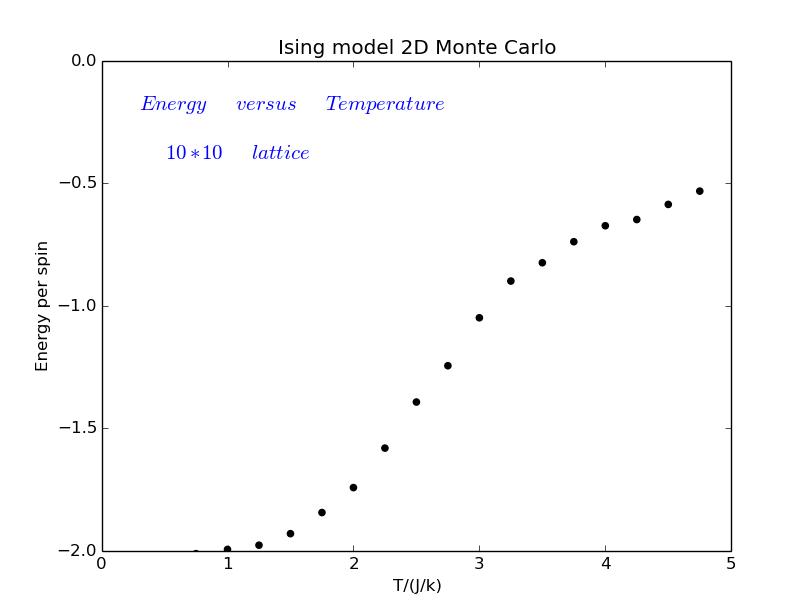
　　The figure shows that the energy per spin increases as temperature increases,and around critical temperture $T_{C}\approx2.27$ the energy per spin increases drastically, which corresponds to a phase transition from ferromagnetic phase to paramagnetic phase.
　　
5、Comparison of Two Methods to calculating 2D Ising model specific heat capacity-temperature relation
　　differential method
　　　　
　　The result shows that around critical temperture $T_{C}\approx2.27$ the mean energy increases drastically.
　　fluctuation-dissipation method$^{[4]}$
　　　　
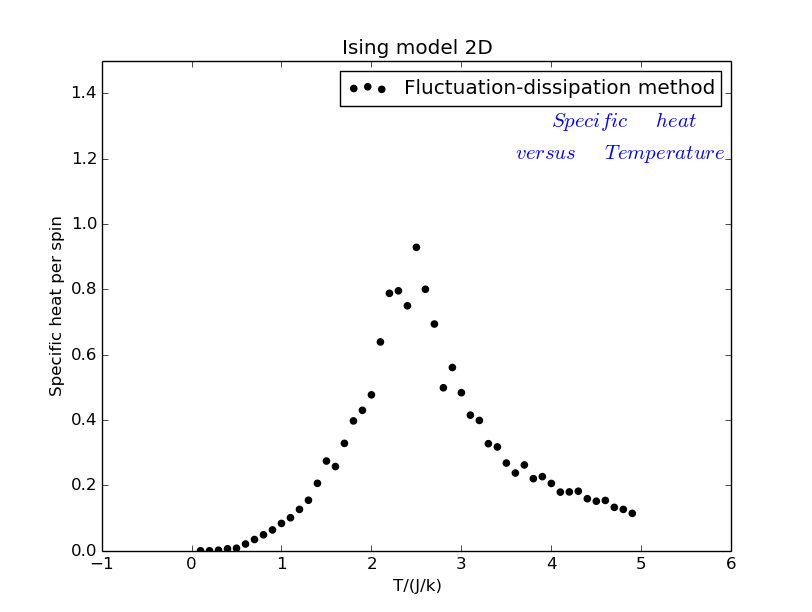
　　We can find that in general the two methods give the same result of specific heat capacity.However,for such noisy data the differential method leads to large uncertainties.
　　Besides,around critical temperture $T_{C}\approx2.27$ the specific heat capacity approaches a peak,which corresponds to a phase transition.
　　　
6、2D Ising model magnetization-time relation
　　　　
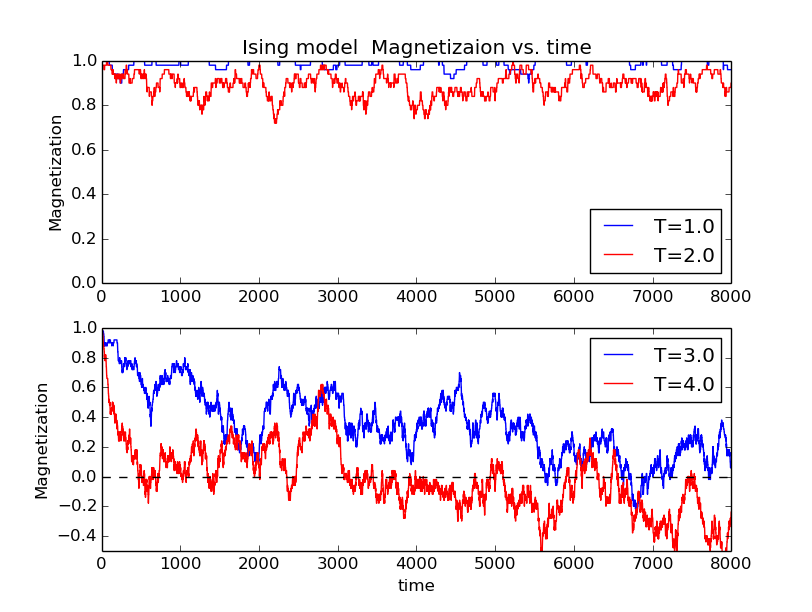
　We can find that as the temperature increases the magnetization decreases,and the fluctuation amplitude of magnetization also increases.
7、2D Ising model magnetization-temperature relation

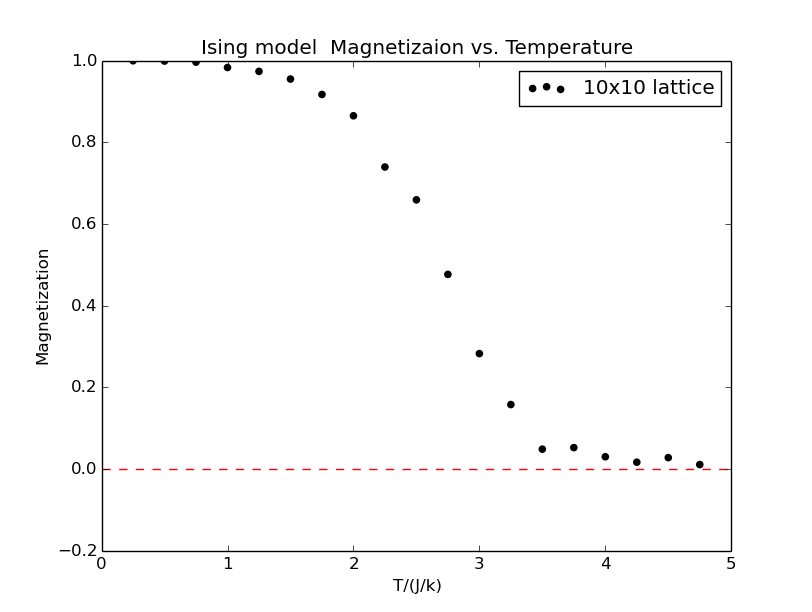
　　The figure shows that the magnetization per spin decreases as temperature increases,and around critical temperture $T_{C}\approx2.27$ the magnetization per spin decreases drastically, which corresponds to a phase transition from ferromagnetic phase to paramagnetic phase.

Conclusion

　　1、The results of one-dimensional Ising model shows that Metropolis algorithm is a powerful method sovling Ising model,whose result corresponds to the analytical result very well.And the result of calculating correlation function is also reasonable.
　　　　The thermodynamics quantities of one-diemensional Ising model are continuous,and there is no phase transition in one-dimensional Ising model.
　　2、The drastical change of mean energy,mean magnetization and the maximum of specific heat capacity around critical temperture $T_{C}\approx2.27$ shows that there is phase transition from ferromagnetic phase to paramagnetic phase.
　　　The two methods to calculate the specific heat capacity give the same result,however, we had better choose the fluctuation-dissipation method which is more accurate.

References

[1] Harvy Gould and Jan Tobochnik. Statistical and Thermal Physics.　New Jersey:Princeton University Press,2010.
[2] C.N. Yang,"The spontaneous magnetization of a two-dimensional Ising model",Phys. Rev. 85,808-816 (1952)
[3] Nicholas J.Giordano. Computational Physics. Beijing：Tsinghua University Press,2007.
[4] Wikipedia. "Ising model". https://en.wikipedia.org/wiki/Ising_model