Chaos in Lorenz Model And Elliptical Billiard Table

     物基一班　 张志城　2013301110121

• 作业L1 3.26
• 作业L2 3.29 3.31
• 作业L3 将以上题目使用vpython进行一个3D展示

Content

Abstract

　　In this passage I solve the Lorenz equations using Euler method,and research how this system reaches chaotic state and the phase space of it .Then I simulate the behavior of a ball bouncing in an elliptical billiard table.I use Vpython to demonstate the 3D visual of both systems.

Background

The Lorenz Model

　　The atmospheric scientist E.N. Lorenz was studying the basic equaitons of fluid mechanics,which are konwn as the Navier-Stokes equations.Because the equations were difficult to solve at that time,Lorenz considered a greatly simplified version of the Navier-Stokes equations as applied to particular problems.He grossly oversimplified the problem as he reduced it to only three equations$^{[1]}$:
　　　　　　　　　$\frac{\mathrm{d} x}{\mathrm{d} t}=\sigma(y-x)$
　　　　　　　　　$\frac{\mathrm{d} y}{\mathrm{d} t}=-xz+rx-y$
　　　　　　　　　$\frac{\mathrm{d} z}{\mathrm{d} t}=xy-bz$
　　Lorenz used $\sigma=10$ and $b=\frac8 3$.In this problem r plays a role analogous to the drive amplitude,$F_{D}$,in the pendulum problem.There are not many exact results for the Lorentz model,but it id known that the transition from steady convection to chaotic behavior takes place at$^{[2]}$:
　　　　$r=\sigma\frac{\sigma+b+3}{\sigma-b-1}=10\times \frac{10+\frac{8}{3}+3}{10-\frac{8}{3}-1}=\frac{470}{19}\approx 24.74$
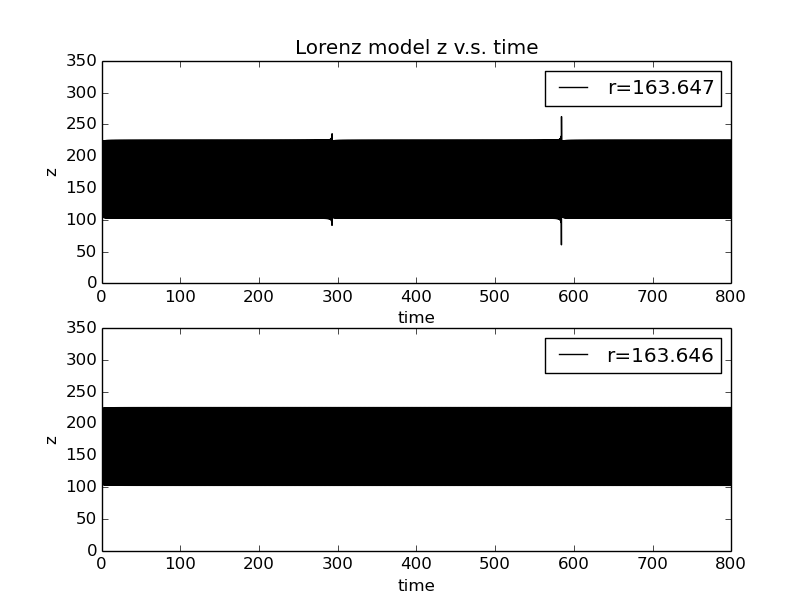
The Lorenz model exhibits period-doubling route to chaos as the pendulum does.At $r=160$ we see periodic oscillations.This corresponds to period-1 behavior.If we choose $r=163.8$,however,the system is transisted to chaos.Here is a threshold value $r_{c}$.When we approach $r_{c}$,but still stay in the chaotic regime,there will be fewer and fewer interludes spaced farther and farther apart.

The Elliptical Billiard Table

　　Except for the collisions with the walls, the motion of the billiard is quite simple.Between collsions the velocity is constant so we have:
　　 　　　　　　$\frac{\mathrm{d} x}{\mathrm{d} t}=v_{x}$
　　 　　　　　　$\frac{\mathrm{d} y}{\mathrm{d} t}=v_{y}$
　　llAnd in the collision,the velocity changes in this way:
　　　　　　　　$\underset{v_{f,\perp }}{\rightarrow}=-v_{i,\perp }$
　　　　　　　　$\underset{v_{f,\parallel }}{\rightarrow}=v_{i,\parallel }$
　　When the table is a circle,the trajectory of the billiard is predictable.However,when the table is not with very high symmertry the system exhibits chaotic behavior.For example,when the table is of a stadium shape or a elliptical shape,the motion becomes sensitive to the initial conditions.

Codes

• the codes for Lorenz model
• the codes for elliptical billiard table

Results

Lorenz Modell

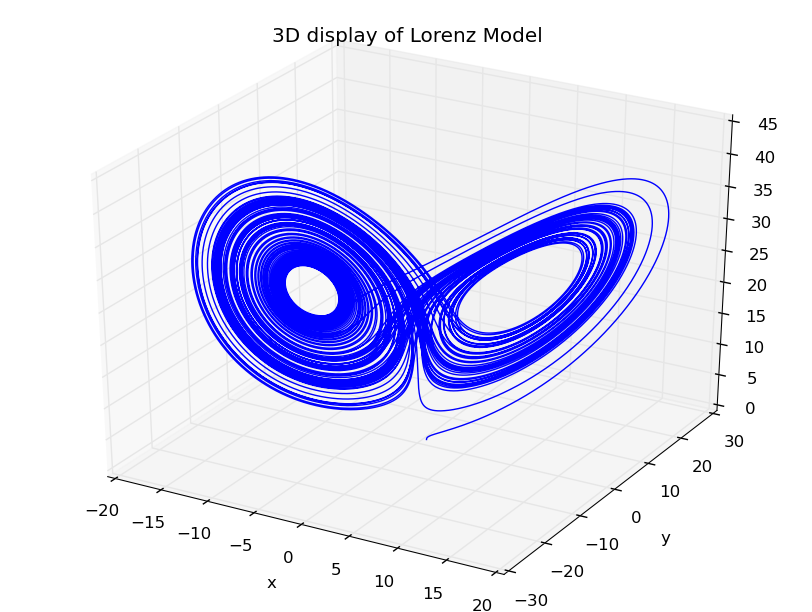
the 3D display of the solution of Lorenz equations

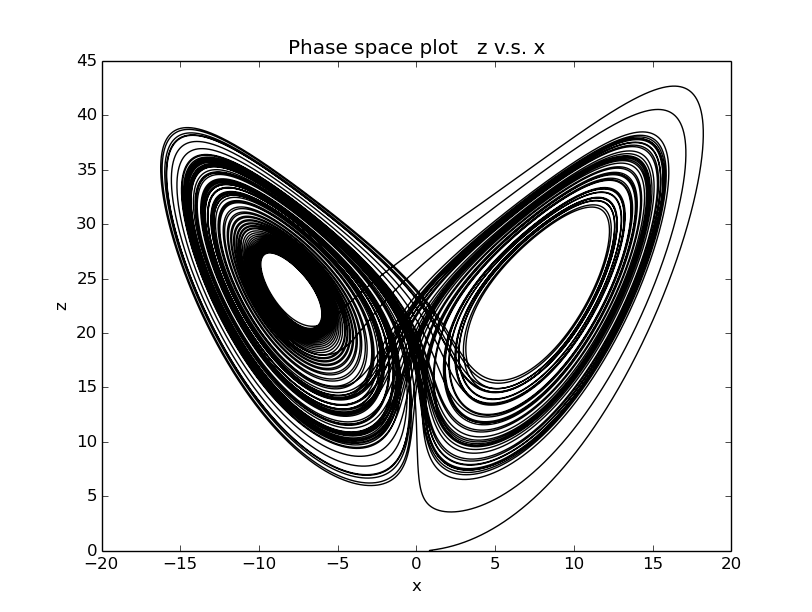
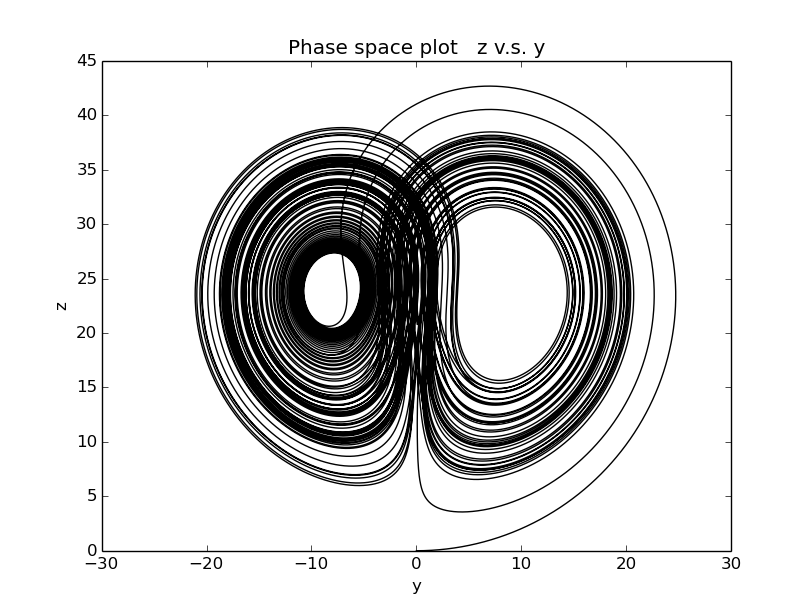
the phase space

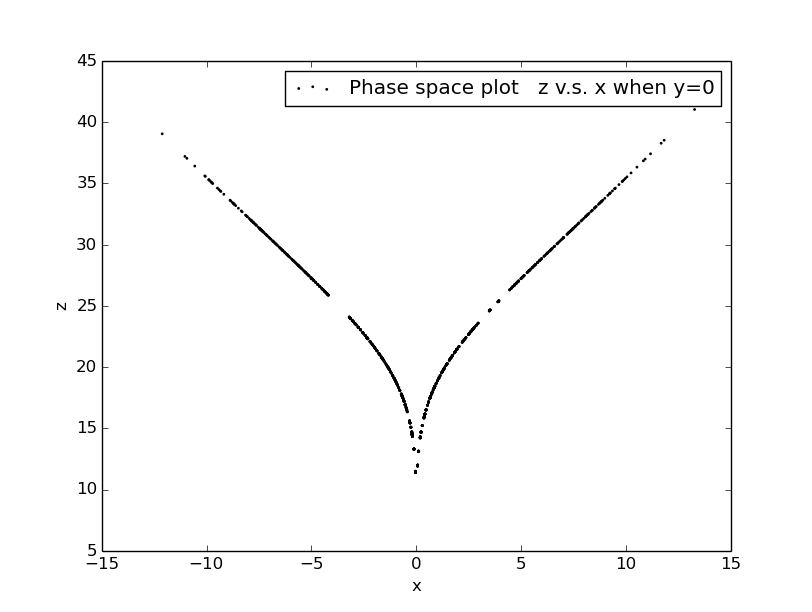
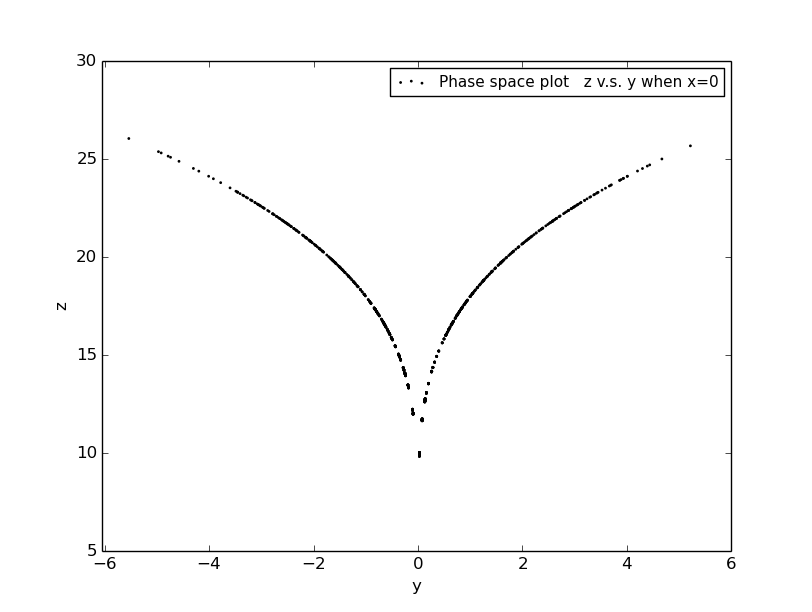
the phase space when one component is fixed

the 3D simulation of Lorenz model

　　If we make (x(t),y(t),z(t)) the coordinate of a ball, the dependence of x,y,z on t will be presented vividly.

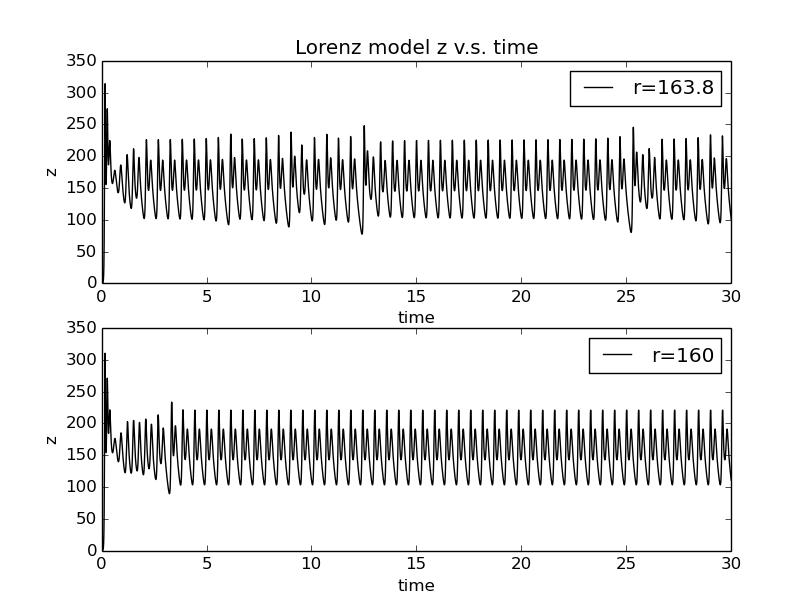
the period behavior of Lorenz model

　　From the picture we can find that when $r=163.647$,there are interludes,but when $r=163.646$there is no interlude in the range $t<=800$.

the Elliptical Billiard Table

　　The elliptical billiard table's parameters:
　　　　$a=20,b=10,center(0,0)$

shoot from origin

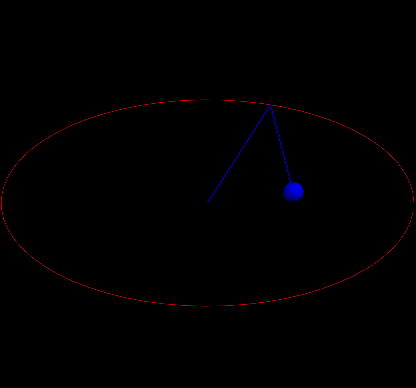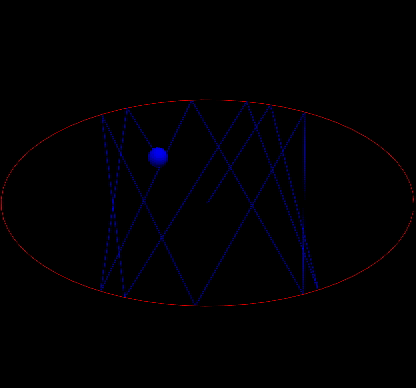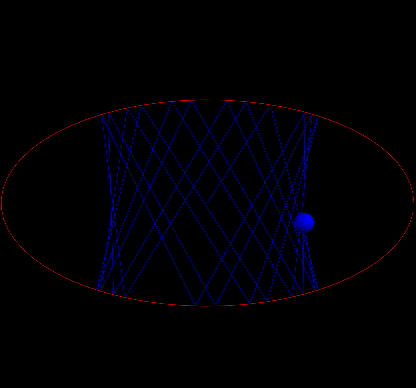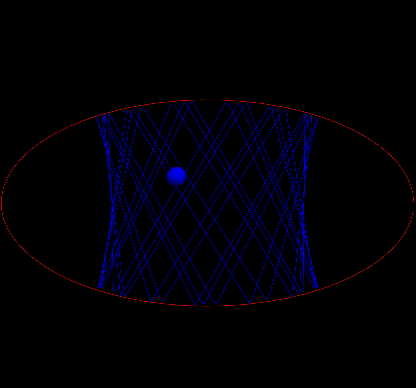
shoot from the focal point

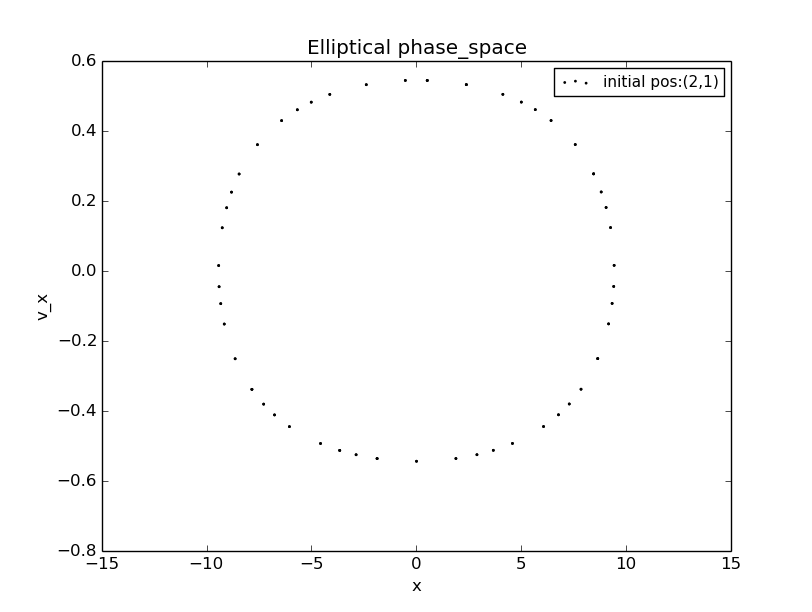
the phase space shooting point(2,1)

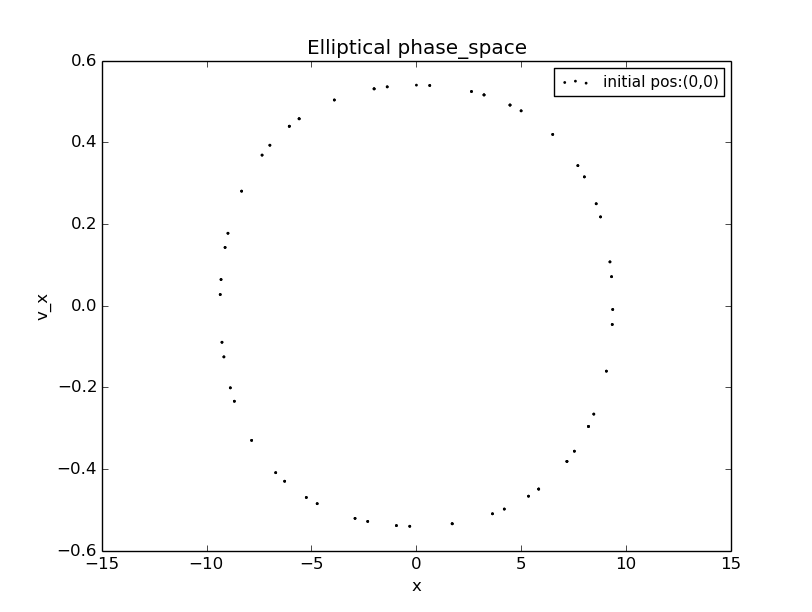
the phase space shooting point(origin)

the phase space shooting point(focal point)

Conclusion

Lorenz Model

　　We can find that when $r=25>24.74$,the system exhibits chaotibehavior.Even though the behavior is strongly chaotic,there is a very high degree of regularity in the phase-space trajectory.Thus we can predict with certainty that the system will be found somewhere on the attractor surface in the phase space.
　　Lorenz model's period behavior is known as the intermittency route to chaos.As the value of $r$decreases,the interludes spaces farther and farther apart.At the transition the spacing between the interludes becomes infinitely long;that is,they no longer occur,and we are left with periodic motion.

Elliptical Billiard

　　From both the animation and the phase-space diagram we can find that the elliptical billiard is a chaotic system.The phase-space plot is reminiscent of the chaotic attractor we find for the pendulum problem.

References

[1] Nicholas J.Giordano. 计算物理. 北京：清华大学出版社,2007.
[2] Wikipedia. https://en.wikipedia.org/wiki/Lorenz_system