Chaotic Tumbling of Hyperion

　　　　　物基一班　张志城　2013301110121

• Exercise 4.20

Contents

Abstract

　　In this passage,I use Euler-Cromer method to simulate a highly simplified model of the smaller moon of Saturn,which does exhibit chaotic behavior.I make use of Vpython to present its motion vividly and verify that its motion is extremely sensitive to initial conditions.

Background

　　Hyperion is one of Saturn's smaller moons,which is extremely small in comparision to other moons.Although due to the interaction between moon's spin and its orbit motion the moon's spin and orbital motion is synchronized,there is an exception in the solar system that doesn't exhibit such synchronism,and the exception is Hyperion.
　　The reason for Hyperion's different behavior is its very unusual shape,together with its highly elliptical orbit.While other moons are approximately spherical,Hyperion is shaped more like an egg with dimensions of about$205\times 130\times110\quad km^{3}$. So it is kind of like an orbiting dumbbell.
　　To simulate the behavior of Hyperion,we had better make a few assumptions first.We consider Hyperion consists of two particles $m_{1},m_{2}$,connected by a massless rod in orbit around a massive object located at the origin.We let $\theta$ be the angle that the rod makes with the x axis and define the associated angular velocity $\omega=\frac{\mathrm{d\theta} }{\mathrm{d} t}$.And after some analysis and calculation,we can get following relation$^{[1]}$:
　　　$\frac{\mathrm{d\omega} }{\mathrm{d} t}\approx-\frac{3GM_{Sat}}{r^{5}_{c}}(x_{c}sin\theta-y_{c}cos\theta)(x_{c}cos\theta+y_{c}sin\theta)$

Codes

• the behavior of Hyperion
• the animation of $\theta-t$ relation
• gravitational spring

Results

the Comparision between Circular And Elliptical Orbit

　　The following gif presents the motion of Hyperion in circular orbit.
　　
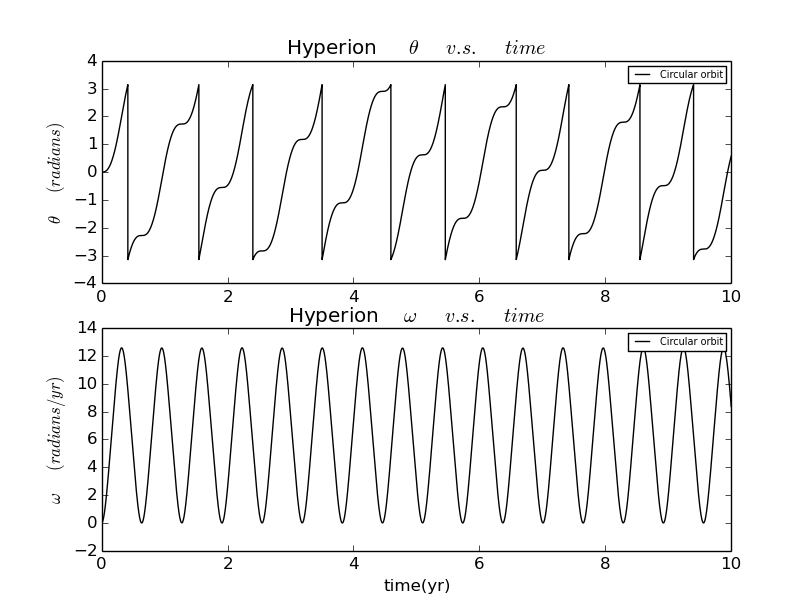
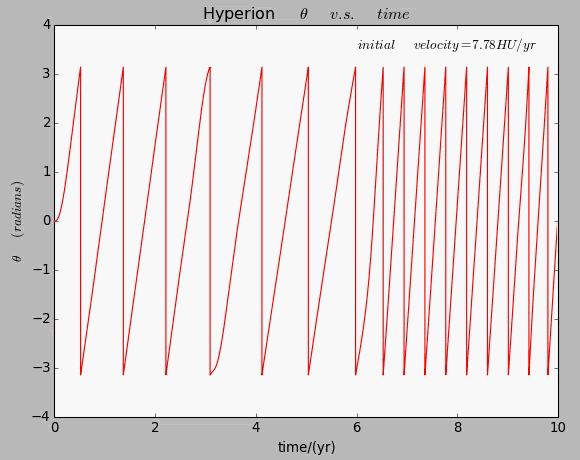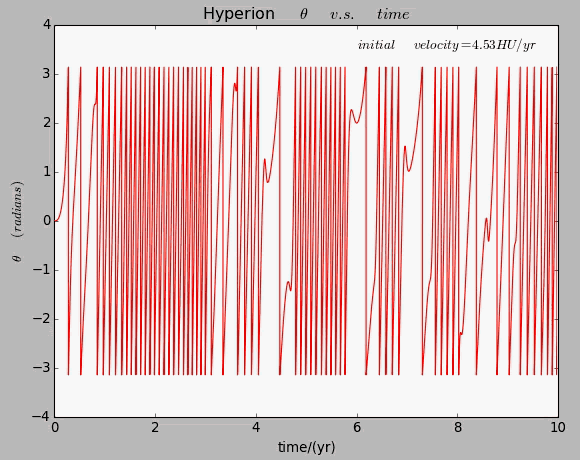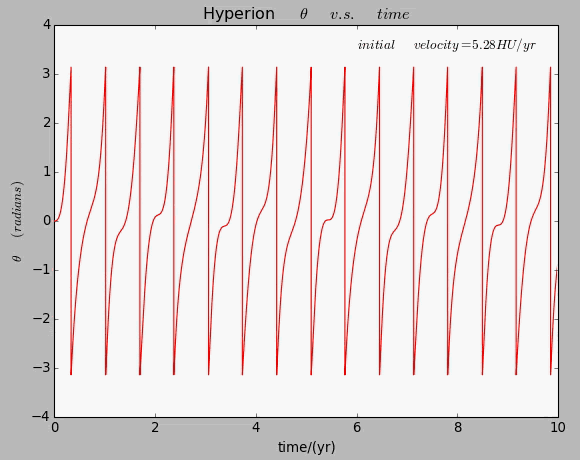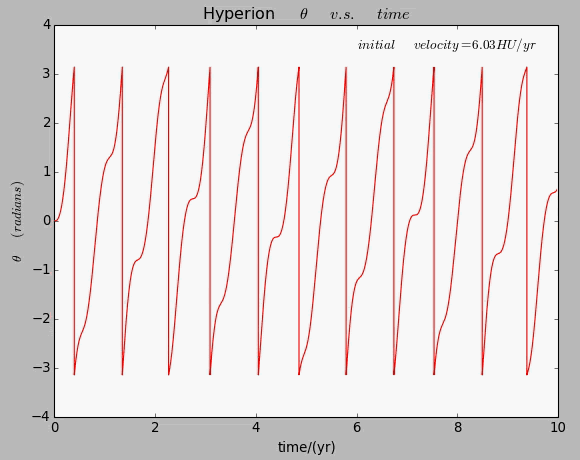
　　And the figure below describes the $\theta-t$ relation and $\omega-t$ relation of Hyperion in a circular orbit,where the initial speed is $2\pi　m/s$.
　　
　　The following gif presents the motion of Hyperion in an elliptical orbit,where the initial speed is $5　m/s$

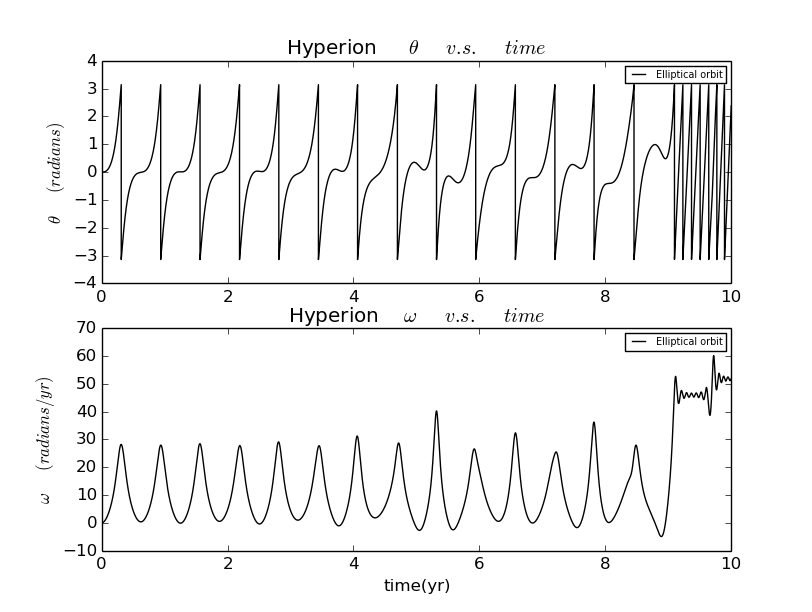
　　And the figure below describes the $\theta-t$ relation and $\omega-t$ relation of Hyperion in an elliptical orbit.
　　
　 Next figure describes the difference of divergence of two nearby trajecories between a circular orbit and an elliptical orbit.I use $\theta_{0}=0$　for one trajectory and $\theta_{0}=0.01$ for another trajectory.
　　
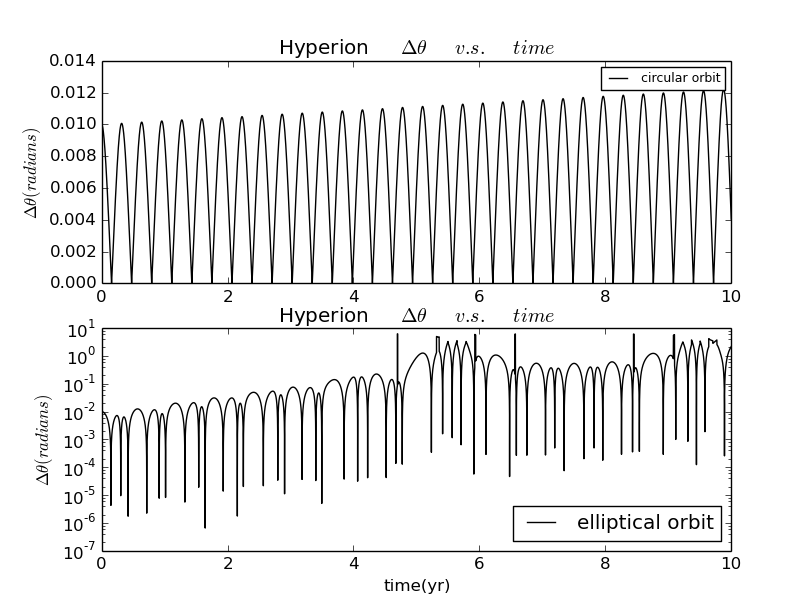
　　The divergence of the elliptical orbit approximately increases with time exponentially.We can find that the circular-orbit motion doesn't exhibit chaotic behavior,while the elliptical-orbit motion exhibits chaotic behavior,which is highly sensitive to initial conditions.
　　Here is an animation$^{[2]}$ shows us how the $\theta-t$ relation will become when the initial velocity of the dumbbell,and thus the eccentricity of the elliptical orbit,changes.
　　

the Reason for Small Dips

　　If we remove the restriction of $\theta$,and repeat the calculation,we can get the following figure:
　　
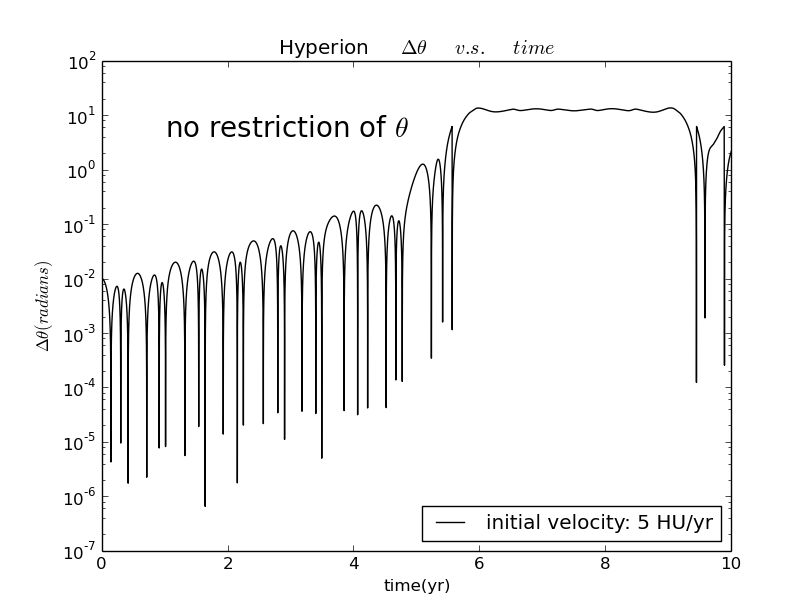
　　Comparing this figure with the figure calculated with restriction of $\theta$,we can find that the jumps about $2\pi$ disappear,but smaller and more frequent dips remain.
　　This situation reminds me of the behavior of a pendulum near one of its turning point.When the dumbbell approaches its turning point,its $theta$ will become small and then large,or first become large and then small.And in both cases,the discrepency between two trajectories will first become small and then large,resulting these frequent dips.

Funny Gravitational Spring

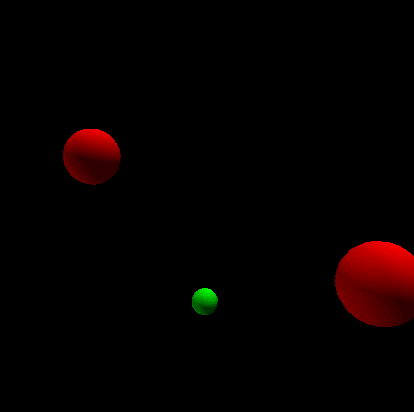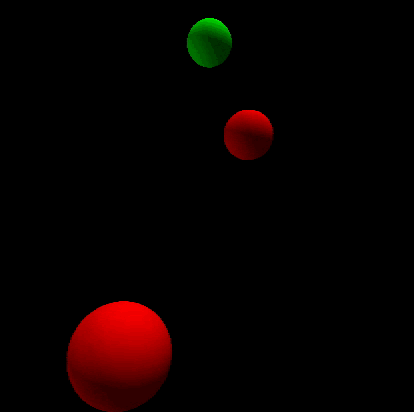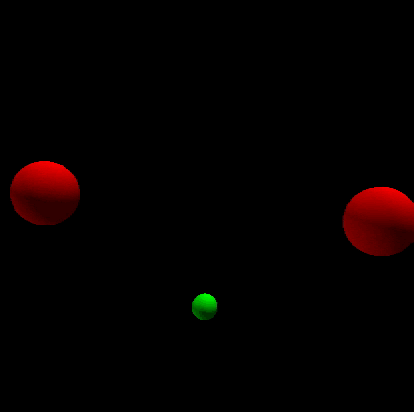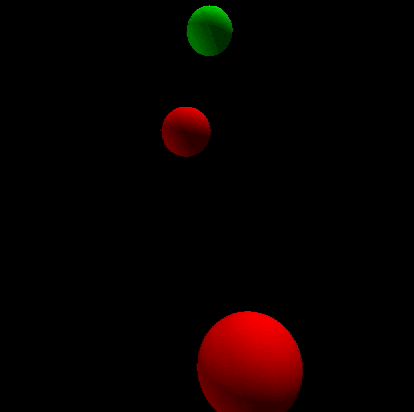
　　The following gif presents the situation:Two massive bodies which have equal mass orbit around the origin.And there is a much smaller body is attracted by the gravitation of the two massive body.So the two massive bodies move in the horizontal plane,and the smaller body move with the line perpendicular to the plane.Here I ignore the effect of the smaller body's gravitation on the two massive bodies.
　　And the behavior of the smaller body is just like that there is an invisible spring which connects it to the origin.
　　

Conclusion

　　Through research above,we can claim that the motion of such an irregularly shaped moon,Hyperion,can be chaotic when its orbit is elliptical.
　　And it is because the dumbbell approaches its turning point and change its rotaion direction that cuases these frequent dips.

References & Acknowledgements

[1] Nicholas J.Giordano. 计算物理. 北京：清华大学出版社,2007.
[2] To accomplish this animation,I refer to the code of Shaosheng Yue (岳绍圣) from his homework