Kepler's Laws & the Precession of the Perihelion of Mercury

　　　　　　　　物基一班　张志城　2013301110121

• Chapter4_problem4.11

Contents

Abstract

　　In this passage,I use Euler-Cromer method to simulate the motion of planets in the solar system which observes the Newton's law of gravity.Specifically,I simulate the motion of the earth and verify that the Kepler's laws applies to it considering the approximations. Besides,I apply general relativity to investigate the precession of the perihelion of Mercury finding that the orbit orientation of Mercury changes linearly with time and the precession rate of a planet increases nonlinearly as its eccentricity increases.
　　

Background

Kepler's Laws

　　Johannes Kepler was a 17th century astronomer who performed a very careful study of the planetary data acquired earlier by Tycho Brahe.Kepler showed that Brahe's observations were consistent with the following three statements:

• All planets move in elliptical orbits,with the Sun at one focus.
• The line joining a planet to the Sun sweeps out equal areas in equal times.
• If $T$ is the period and $a$ the semimajor axis of the orbit,then $\frac{T^{2}}{a^{3}}$ is a constant.

　　Now we know that all these laws can be derived form Newton's law of universal gravitation:
　　　　　　　　$F_{G}=\frac{GM_{S}M_{P}}{r^{2}}$　　(4.1.1)

Planetary Motion in Central Field

　　Let's then discuss some features of planetary motion in central field.

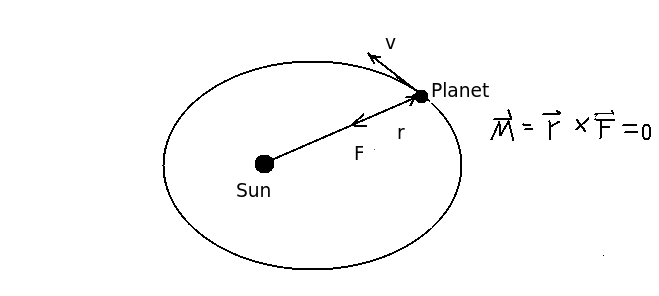
　　1. As is shown in the figure,there is no momentum in the central field.Thus we have
　　　　　　　　　$\frac{\mathrm{d\mathbf{J}} }{\mathrm{d} t}=\mathbf{M}=0$　　 (4.1.2)
It means that in the central field the angular momentum is conserved.
　　In a polar coordinates,the angular momentum is
　　　　　　　　　$J=mr^{2}\dot{\theta}=J_{0}$　　(4.1.3)
And the angular momentum per unit mass is
　　　　　　　　$r^{2}\dot{\theta}=h\, \,(constant)$　　(4.1.4)
　　2.Since work done by gravity is path-independent,the gravitation field is conservative field$^{[1]}$. So the mechanical energy of the system is conserved. Namely,
　　　　　　$\frac{1}{2}m(\dot{r}^{2}+r^{2}\dot{\theta}^{2})+V(r)=E_{0}$　　(4.1.5)
　　4.From Newton's law of universal gravity,we can get the motion eqaution of the planet:
　　　　　　　　$m(\ddot{r}-r\dot{\theta}^{2})=F(r)$　　(4.1.6)
　　5.We can get from equation (4.1.3) and (4.1.6) that the orbit of the planet is$^{[2]}$
　　　　　　　　$r=(\frac{L^{2}}{\mu GM_{S}M_{P}})\frac{1}{1-ecos\theta}$　　(4.1.7)
When $0<e<1$, the orbit is an ellipse,which is what Kepler's first law describes.
　　6.The area the planet sweeps during a time interval $dt$
is
　　　　　　$\frac{\mathrm{dA} }{\mathrm{d} t}=\frac{1}{2}r^{2}d\theta=\frac{1}{2}h\,\,(constant)$　　(4.1.8)
This is the content of Kepler's second law.
　　7.If we integrate both sides of equation (4.1.8),we will get that$^{[3]}$
　　　　　　　　$\int dA=\frac{1}{2}h\int dt$　　(4.1.9)
　　　　　　　　　$T=\frac{2\pi a^{\frac{3}{2}}}{k}$　　(4.1.10)
This is the Kepler's third law.

the Precession of Mercury's Perihelion

　　Although Kepler's laws describe the planetary motion well, there are deviations from these laws. For Mercury it was known by the early part of the 19th century that the orientation of the axes of the ellipse that describes its orbit rotate with time.The magnitude of precession is approximately 566 arcseconds per century.Despite 523 arcseconds of them can be expalined by the effect of other planets,there are still 43 arcseconds remained as a mystery.It was not until 1917 that Einstein developed the theory of general relativity and sloved the problem.And the force law predicted by general relativity is
　　　　　　　$F_{G}\approx\frac{GM_{S}M_{M}}{r^{2}}(1+\frac{\alpha}{r^{2}})$　　(4.1.11)

Codes

• codes of 'Kepler's Law'
• codes of 'Precession of Mercury's perihelion'

Results

Verify Kepler's Law

　　I take these initial values:　 $GM_{S}=4\pi\,\,AU^{3}/yr^{2},r_{min}=1AU,v_{max}=2.3\pi AU/yr$　　(4.1.12)

1.　We can calculate that
　　　　　$E_{0}=-\frac{GM_{S}}{2a}=-1.355\pi$
　　　　　$e=\sqrt{1+\frac{2E_{0}h^{2}}{mG^{2}M_{S}^{2}}}=0.3225$　　(4.1.13)
Thus
　　　　　$r_{max}/r_{min}=\frac{1+e}{1-e}\approx1.9520$　　(4.1.14)
　　And the result of the simulation gives the value $1.9521,$which differs from theoretical result only at an extent of $0.0051\%$. It verifies the Kepler's first law.

2.　Using the initial parameters,we can calculate the angular momentum per unit mass 　
　　　　　　　　$h=r_{min}v_{max}=7.225663AU^{2}/yr.\,$
　　And the simulation result is shown below,which gives the same result.From the gif we can find that $h$ remains as a constant,which verifies the Kepler's second law.

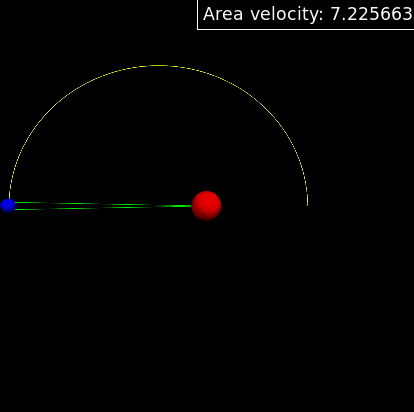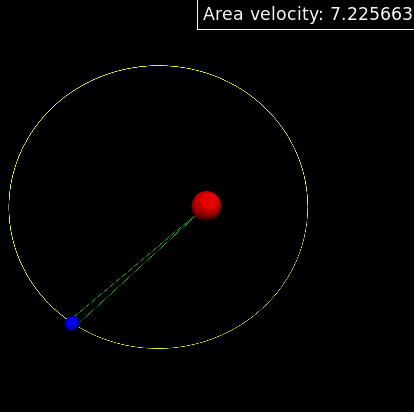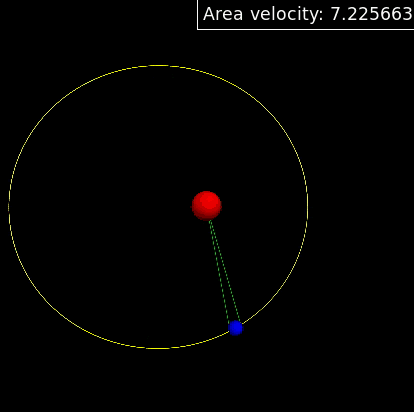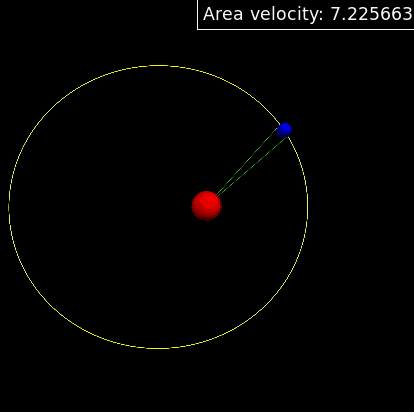
3.　From equation (4.10) we can get that the period of the system is $1.793$, and the simulation gives the same value,which verifies the Kepler's third law.

the Precession of Mercury's Perihelion

　　If we use equation (4.1.11) to simulation Mercury's motion, we will get following result.To simulate the real motion of Mercury, the parameters are 　$r_{max}=0.47034AU,v_{min}=2.59857\pi AU/yr,\,\alpha=0.0008$
　　
　　　　

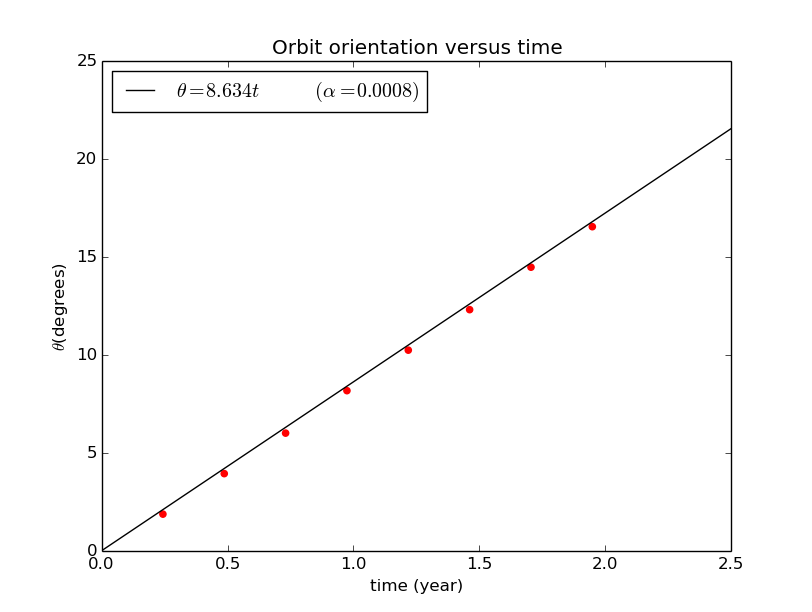
　　And we can find that the orbit orientation of Mercury varies with time in following way.The figure shows that the precession of the perihelion is almost linearly dependent on time,which is consistent with observations.
　　　　

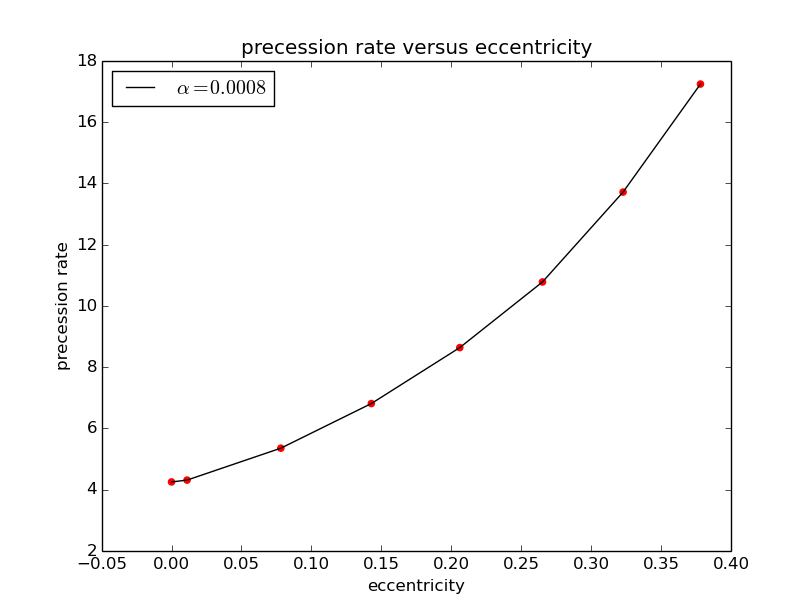
　　If we change the initial velocity $v_{min}$ ,we therefore change the eccentrity and manage to keep the aphelion unchanged. Then we can study the relation between eccentricity and the precession rate.And I get following result.We can find that precession rate increases nonlinearly with eccentricity:the greater the eccentricity is,the faster precession rate gets.
　　
　　　　

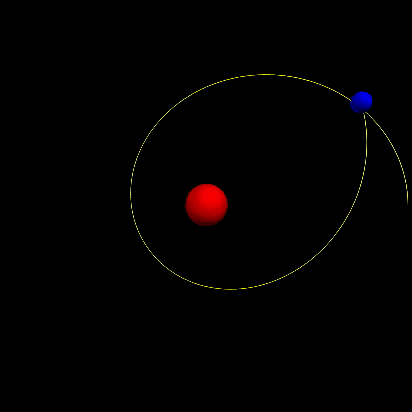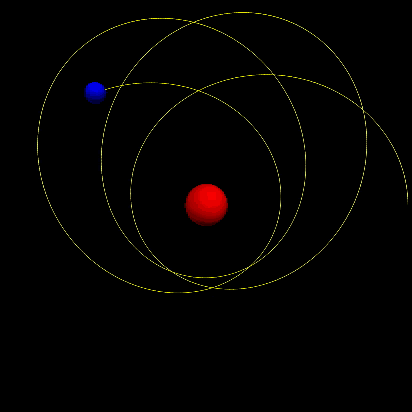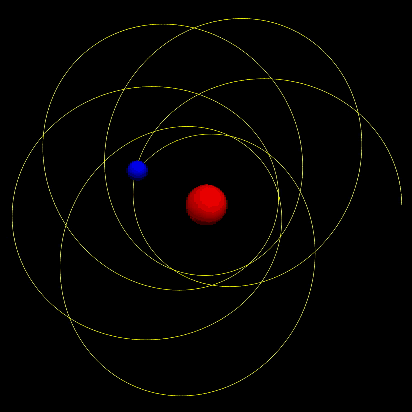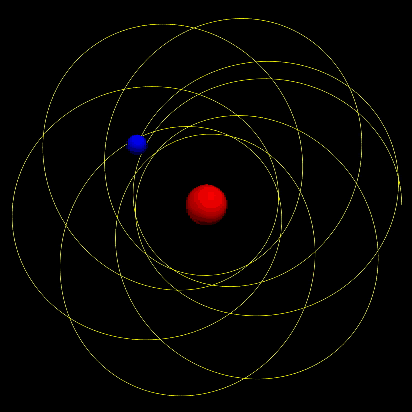
　　For $\alpha=0.01,v_{min}=2.3\pi AU/yr$,we can get following motion pattern which shows obvious precession of the perihelion.
　　
　　　　

Conclusion

　　In general,all of the Kepler's laws are verified since as is shown in the 'result' section that the motion of the planet is described and predicted by the Kepler's law at a quite high accuracy.
　　We can find that the precession of the perihelion of Mercury increases approximately linearly with time.Besides,the precession rate increases nonlinearly with eccentricity:the greater the eccentricity is,the faster precession rate gets. Futhermore,for larger value of $\alpha$,the precession becomes more obvious.

References

[1]　Wikipedia. https://en.wikipedia.org/wiki/Conservative_vector_field
[2]　Nicholas J.Giordano. 计算物理. 北京：清华大学出版社,2007.
[3]　许定安等. 经典力学. 武汉：武汉大学出版社,1996.