线性分类器-1

pattern-recognition machine-learning

---

线性 = 齐次性 + 可加性，即$f(x)$被称为线性函数如果：
1. $f(ax)=af(x)$
2. $f(a+b)=f(a)+f(b)$

• 对一个数值向量$\mathbf{x}$, 其线性函数可以写成$y(\mathbf{x})=\mathbf{w}^{\mathrm{T}} \mathbf{x}+w_{0}$
• 如果以$y(\mathbf{x})\geq0$或$y(\mathbf{x})<0$作为分类标准，这个分类器就叫做线性分类器
• 如何求$\mathbf{w}$和$w_{0}$，就引出了几种不同的线性分类器模型

1. Minimum Square Error (MSE)

和线性回归中的MSE方法类似，MSE线性分类器希望自己给出的判别结果与数据标签之间的误差平方和（sum-of-square error）尽可能小。考虑一个$K$类分类问题，每个样本属于其中一类，如果用one-hot向量编码样本的分类，每个样本对应一个$\mathbf{t}=(0,0,...,1,...,0)^\mathrm{T}$的$K$维向量，$N$个样本的$\mathbf{t}^{\mathrm{T}}$组成的$\mathbf{T}_{N\times K}$，就是模型需要逼近的目标，即

$$E_{D}(\widetilde{\mathbf{W}})=\frac{1}{2} \operatorname{Tr}\left\{(\widetilde{\mathbf{X}} \widetilde{\mathbf{W}}-\mathbf{T})^{\mathrm{T}}(\widetilde{\mathbf{X}} \widetilde{\mathbf{W}}-\mathbf{T})\right\}$$

这里为了方便把$\mathbf{w}^{\mathrm{T}} \mathbf{x}+w_{0}$写成一个矩阵乘积的形式，也就是$\widetilde{x}=(1,x)$，$\widetilde{w}=(w_0,\mathbf{w})$，也叫增广向量。而矩阵$\widetilde{\mathbf{X}}_{N\times D}$是样本增广向量拼成的，矩阵$\widetilde{\mathbf{W}}_{D\times K}$是$K$个判别向量拼成的。

要解出$\widetilde{\mathbf{W}}$，只需要令$\frac{\partial E_{D}(\widetilde{\mathbf{W}})}{\partial{\widetilde{\mathbf{W}}}}=\mathbf{0}$，解得

$$\widetilde{\mathbf{W}}=\left(\widetilde{\mathbf{X}}^{\mathrm{T}} \widetilde{\mathbf{X}}\right)^{-1} \widetilde{\mathbf{X}}^{\mathrm{T}} \mathbf{T}=\widetilde{\mathbf{X}}^{\dagger} \mathbf{T}$$

此处的$\widetilde{\mathbf{X}}^{\dagger}$是$\widetilde{\mathbf{X}}$的Moore-Penrose广义逆矩阵

解得$\widetilde{\mathbf{W}}$后，我们可以给每个样本预测一个标签向量$\mathbf{y}(\mathbf{x})=\widetilde{\mathbf{W}}^{\mathrm{T}} \widetilde{\mathbf{x}}=\mathbf{T}^{\mathrm{T}}\left(\widetilde{\mathbf{X}}^{\dagger}\right)^{\mathrm{T}} \widetilde{\mathbf{x}}$，是一个$K$维向量，可以取其中最大的一维作为预测结果

需要注意：

• 这个向量不适合作为概率表示，因为没有限制值在$(0,1)$之间
• 与MSE线性回归类似，该方法对outliers非常敏感
• Logistic Regression可以解决上述两个问题
• it corresponds to maximum likelihood under the assumption of a Gaussian conditional distribution

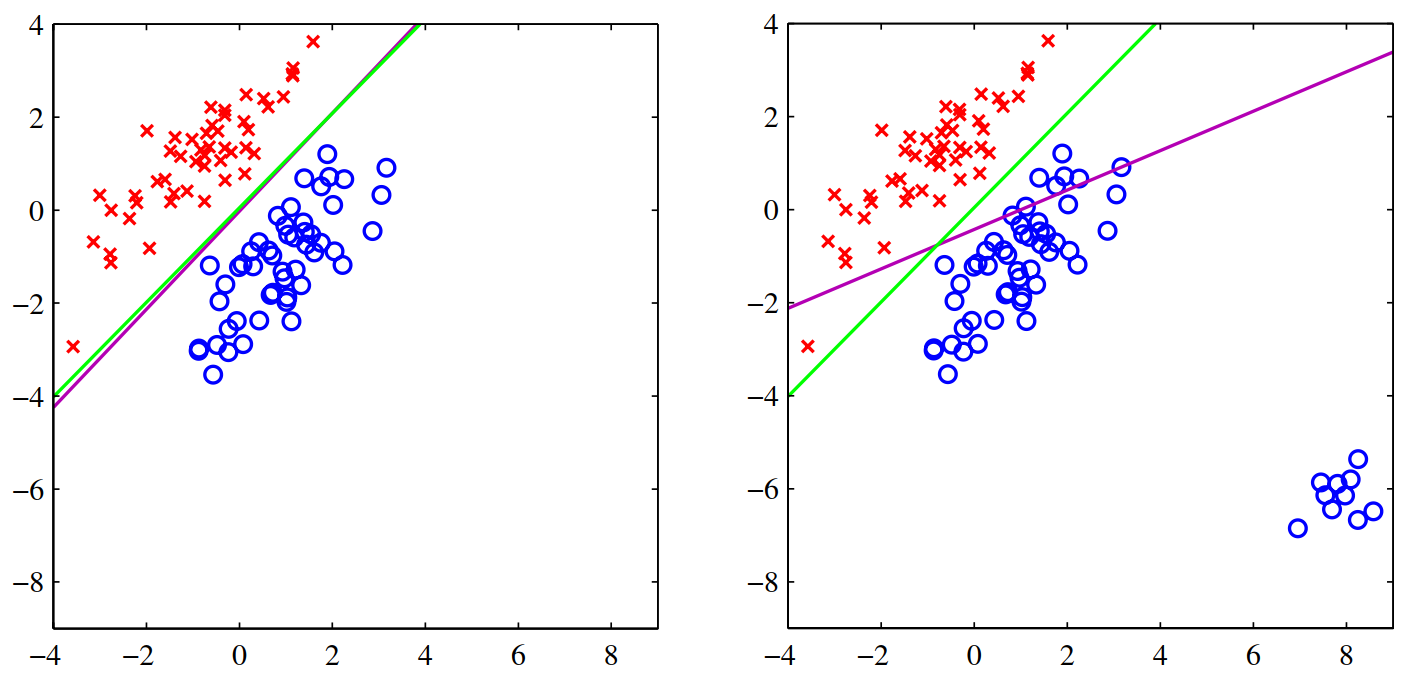
该图展示了MSE对outlier敏感的特点，左右两张图中，绿线是Logistic regression的结果，紫线是MSE的结果

2. Fisher's Linear Discriminant (FLD)

如果把线性判别看作一个降维问题，其实就是将高维数据降到一维，再用一个阈值对两类进行区分，而$\mathbf{w}$的选择就是选择一个降维方向，使得降维后各类能最大程度地分开。当考虑有两类，一个很直观的想法是，我们会希望降维后两类的均值差尽可能大，而各自的方差尽可能小，即

$$J(\mathbf{w})=\frac{\left(m_{2}-m_{1}\right)^{2}}{s_{1}^{2}+s_{2}^{2}}$$
这里的$m_i=\frac{1}{N_i}\sum_{n \in \mathcal{C}_{i}}\mathbf{w}^{\mathrm{T}}\mathbf{x}_n$， $s_{i}^{2}=\sum_{n \in \mathcal{C}_{i}}\left(\mathbf{w}^{\mathrm{T}}\mathbf{x}_n-m_{i}\right)^{2}$

稍微变换一下形式我们得到（其实就是把$m_i$和$s_i$代入）

$$J(\mathbf{w})=\frac{\mathbf{w}^{\mathrm{T}} \mathbf{S}_{\mathrm{B}} \mathbf{w}}{\mathbf{w}^{\mathrm{T}} \mathbf{S}_{\mathrm{W}} \mathbf{w}}$$
这里的$S_B$和$S_W$分别叫类间散度（between-class covariance）和类内散度(within-class covariance)，有如下形式
$$\mathbf{S}_{\mathrm{B}}=(\mathbf{m _ { 2 }}-\mathbf{m _ { 1 }})(\mathbf{m _ { 2 }}-\mathbf{m _ { 1 }})^{\mathrm{T}}$$
$$\mathbf{S}_{\mathrm{W}}=\sum_{n \in \mathcal{C}_{1}}\left(\mathbf{x}_{n}-\mathbf{m}_{1}\right)\left(\mathbf{x}_{n}-\mathbf{m}_{1}\right)^{\mathrm{T}}+\sum_{n \in \mathcal{C}_{2}}\left(\mathbf{x}_{n}-\mathbf{m}_{2}\right)\left(\mathbf{x}_{n}-\mathbf{m}_{2}\right)^{\mathrm{T}}$$
注意这里都是原空间的样本向量和均值向量，顺带一提这两个散度加起来等于全样本散度

考察目标函数$J(\mathbf{w})$发现，分子分母可以随意同比例缩放，所以不如固定分等母于一个常值$C$，求分子的最大值，就变成带约束的优化问题，用拉格朗日乘子法解

$$L(\mathbf{w})=\mathbf{w}^{\mathrm{T}} \mathbf{S}_{\mathrm{B}}\mathbf{w}+\lambda (\mathbf{w}^{\mathrm{T}} \mathbf{S}_{\mathrm{W}} \mathbf{w}-C)$$

令$L(\mathbf{w})$对 $\mathbf{w}$ 的偏导为0，解得

$$\mathbf{S}_{\mathrm{B}}\mathbf{w}+\lambda \mathbf{S}_{\mathrm{W}} \mathbf{w}=0$$

把$\mathbf{S}_{\mathrm{B}}=(\mathbf{m _ { 2 }}-\mathbf{m _ { 1 }})(\mathbf{m _ { 2 }}-\mathbf{m _ { 1 }})^{\mathrm{T}}$代入发现，$(\mathbf{m _ { 2 }}-\mathbf{m _ { 1 }})^{\mathrm{T}}\mathbf{w}$ 是个标量，$\lambda$也是个标量，而我们要找的是投影方向，标量并不影响向量的方向，所以

$$\mathbf{w}=-\lambda (\mathbf{m _ { 2 }}-\mathbf{m _ { 1 }})^{\mathrm{T}}\mathbf{w}\mathbf{S}_{\mathrm{W}}^{-1}(\mathbf{m _ { 2 }}-\mathbf{m _ { 1 }})\propto \mathbf{S}_{\mathrm{W}}^{-1}\left(\mathbf{m}_{2}-\mathbf{m}_{1}\right)$$

即$\mathbf{S}_{\mathrm{W}}^{-1}\left(\mathbf{m}_{2}-\mathbf{m}_{1}\right)$ 是FLD的一个解

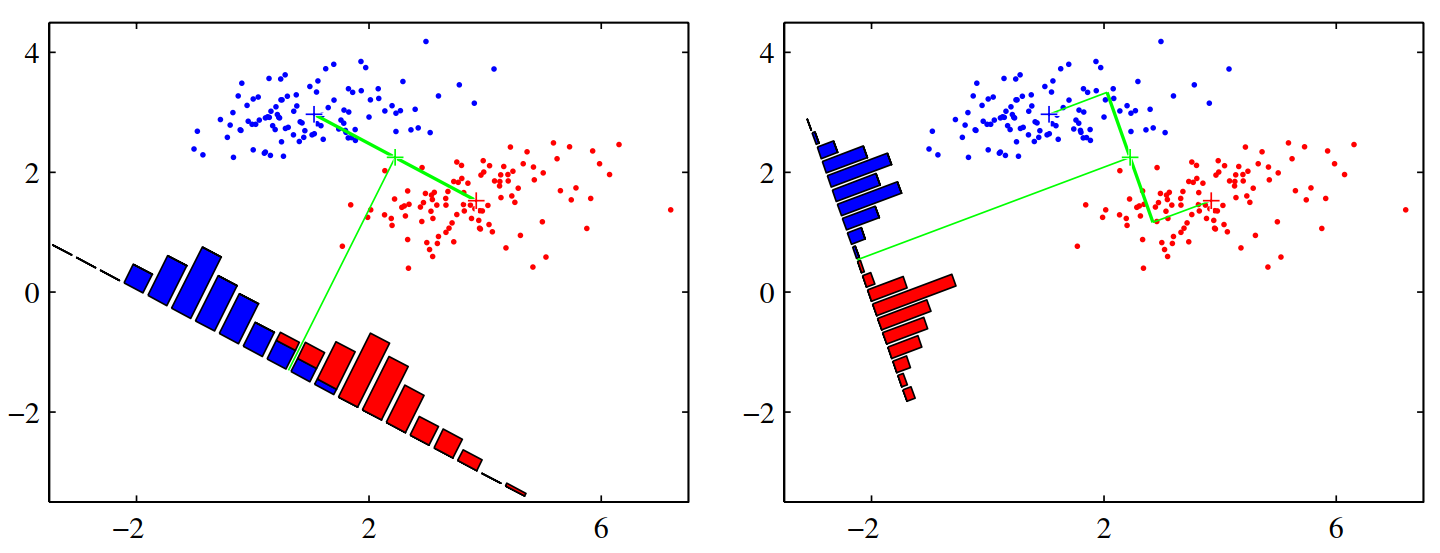
FLD示意图，对于同一批数据，显然右图的降维方式会使得数据在低维空间更可分

需要注意：

• FLD实际上并不是一个判别式 (discriminant)，而是把数据降到一维的策略
• 但是一维的数据通过设定阈值可以得到一个判别式
• 当数据只有两类，FLD和MSE方法得到的结果是一致的，但是MSE里的 $\mathbf{t}$ 向量的值需要从1和-1变成$N/N_1$和$-N/N_2$，$N_1, N_2$分别是两类的样本数量 (Duda and Hart, 1973. PRML, Page.190)
• 当数据有多类，或需要将数据降到不止一维，FLD都可以扩展，多类的扩展相当显而易见，而多维的扩展中，目标函数是
  $$J(\mathbf{W})=\operatorname{Tr}\left\{\mathbf{s}_{\mathrm{W}}^{-1} \mathbf{s}_{\mathrm{B}}\right\}=\operatorname{Tr}\left\{\left(\mathbf{W} \mathbf{S}_{\mathrm{W}} \mathbf{W}^{\mathrm{T}}\right)^{-1}\left(\mathbf{W} \mathbf{S}_{\mathrm{B}} \mathbf{W}^{\mathrm{T}}\right)\right\}$$
  后续的求解其实也差不多
• 有趣的是，如果数据有 $K$ 类，由于$\mathbf{S}_{\mathrm{B}}$至多有 $K-1$ 个自由度，也就最多只能找到 $K-1$ 个降维方向 (Fukunaga, 1990)

3. 感知机 (Perceptron)

感知机与上面两种方法不同，其没有闭式解，而是通过训练迭代的方法使 $\mathbf{w}$ 收敛到最优解。这种方法更像是“学习”的过程，感知机也在后来成为了神经网络的基本结构——神经元 (neurons)。

感知机的算法相当简单，假设数据 $\mathbf{x}$ 经过某些线性或非线性变换，变成了特征向量 $\phi(\mathrm{x})$ ，再对 $\phi(\mathrm{x})$ 建立线性模型，这也叫对 $\mathbf{x}$ 的广义线性模型：

$$y(\mathbf{x})=f\left(\mathbf{w}^{\mathrm{T}} \boldsymbol{\phi}(\mathbf{x})\right)$$
这里的$f(\cdot)$是一个激活函数，把线性变换的结果映射成分类标签，我们就用最简单的
$$f(a)=\left\{\begin{array}{ll}{+1,} & {a \geqslant 0} \\ {-1,} & {a<0}\end{array}\right.$$

现在我们有两类数据，分别标记成1和-1，用 $t_n$ 表示，我们希望 $y(\mathbf{x})$ 在1类中尽可能大，在-1类中尽可能小，则目标函数如下

$$E_{\mathrm{P}}(\mathbf{w})=-\sum_{n \in \mathcal{M}} \mathbf{w}^{\mathrm{T}} \boldsymbol{\phi}_{n} t_{n}$$
注意这里的 $\mathcal{M}$ 表示分类错误的样本集，即我们只看错误的部分，已经分类正确的就不管了。如果用梯度下降的方式，会得到
$$\mathbf{w}^{(\tau+1)}=\mathbf{w}^{(\tau)}-\eta \nabla E_{\mathrm{P}}(\mathbf{w})=\mathbf{w}^{(\tau)}+\eta \sum_{n \in \mathcal{M}}\phi_{n} t_{n}$$

这就是更新公式了，反复更新 $\mathbf{w}$ ，使其最终收敛，就能得到判别方程。

该图示意感知机的判别机制

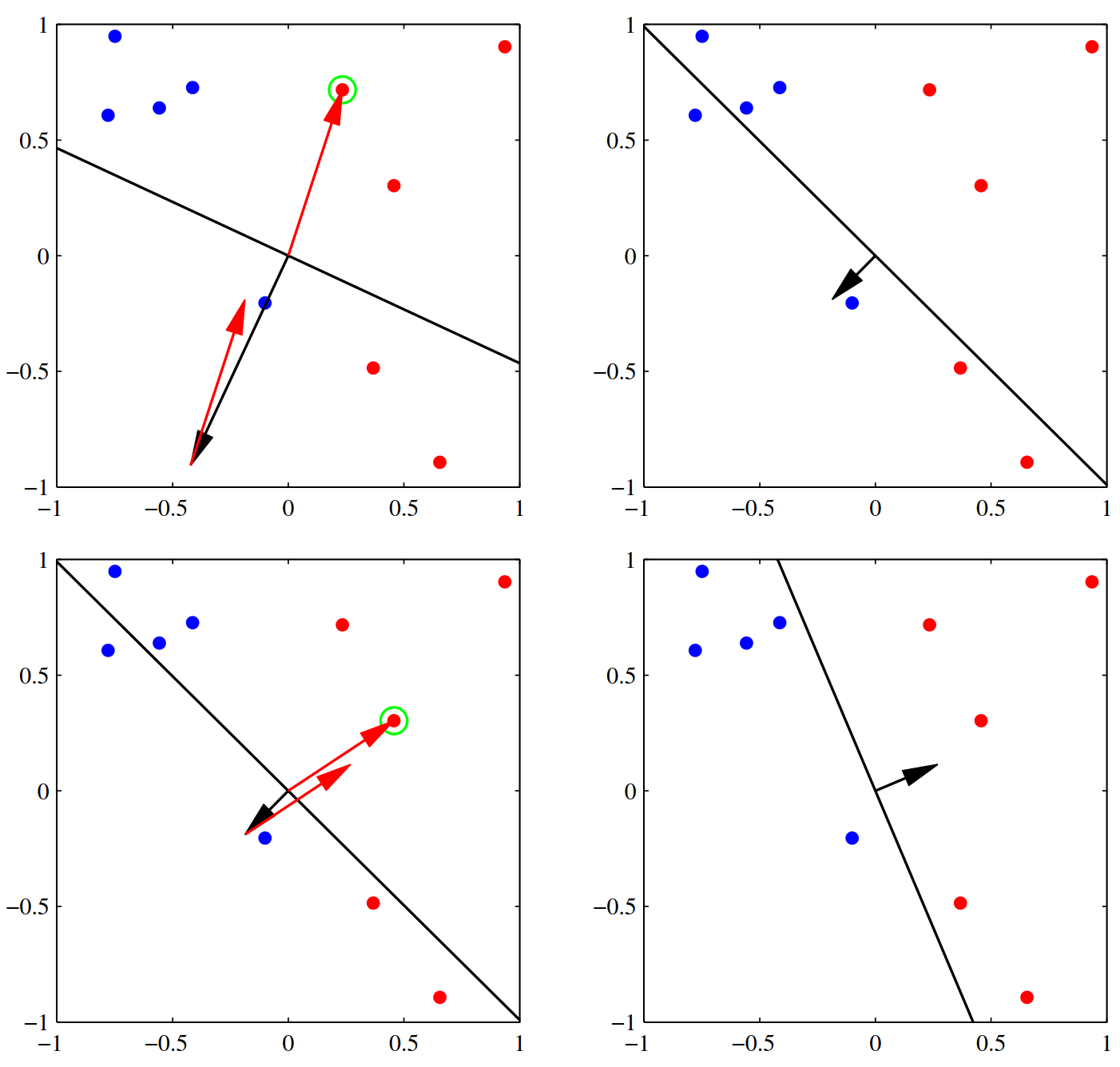
该图示意感知机的迭代收敛过程

需要注意：

• perceptron convergence theorem 证明了如果样本是线性可分的，感知机一定能在有限次迭代里收敛到一个正确的解上
• 一般为了收敛更快，一般人们使用随机梯度下降 (stochastic gradient descent, SGD)，即$\mathbf{w}^{(\tau+1)}=\mathbf{w}^{(\tau)}+\eta \phi_{n} t_{n}$，收敛理论也有效
• 如果数据线性不可分，显然该算法就无法收敛
• 但是收敛之前，我们无法从训练曲线上看出来它到底是收敛得慢，还是数据本身线性不可分
• 线性可分的数据可能有多个解，具体感知机会收敛到哪一个，取决于初值的设定（神经网络黑盒子的毛病已经初见端倪）
• 感知机出现的几乎同时，还有一个叫 adaline 的算法，模型和感知机几乎一样，但是迭代策略有所不同