NNLM & Word2vec

deep-learning representation-learning NLP pre-trained-model

---

(NNLM paper) Y. Bengio, R. Ducharme, P. Vincent. A neural probabilistic language model. Journal of Machine Learning Research, 3:1137-1155, 2003.

(word2vec paper) Tomas Mikolov, Kai Chen, Greg Corrado, and Jeffrey Dean. Efficient estimation of word representations in vector space. ICLR Workshop, 2013.

Representation of Words

• atomic units: represented as indices in a vocabulary
  
  • simplicity, robustness, better than complex systems
  • no notion of similarity between words
  • no pre-training: data for some special task are limited (speech recognition)
    

---

• Distributed representations
  
  • neural network language model (NNLM)
  • other followers of NNLM
  • Word2vec

NNLM

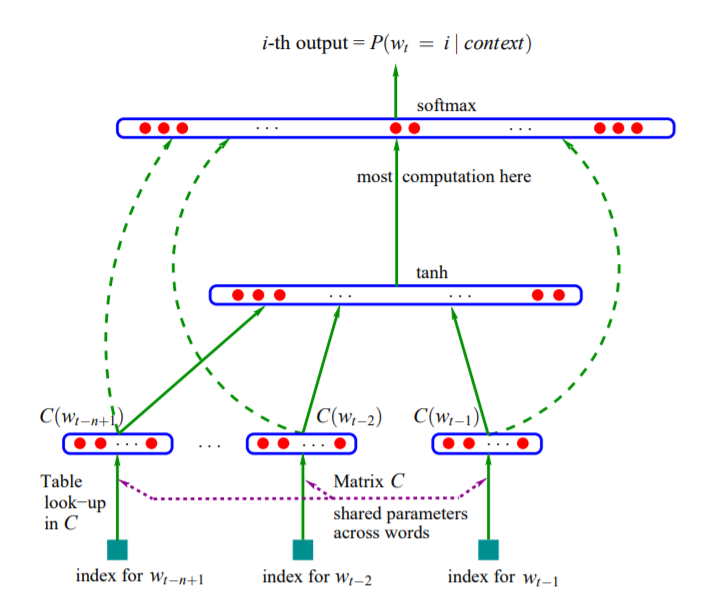
1. word indices extract a D dimentional vector from a shared projection matrix
2. N words' vectors are projected to hidden layer, with H hidden units and a tanh non-linear activation
3. output layer calculate softmax probability of each word in the vocabulary
4. predict a word Wt using its previous n words

Objective function:

$$L=\frac{1}{T} \sum_{t} \log f\left(w_{t}, w_{t-1}, \cdots, w_{t-n+1} ; \theta\right)+R(\theta)$$
where $f\left(w_{t}, w_{t-1}, \cdots, w_{t-n+1} ; \theta\right)=\hat{P}\left(w_{t} | w_{1}^{t-1}; \theta\right)$ is the probability that given $w_{t-1}, \cdots, w_{t-n+1}$, the model can predict the right word $w_t$. $R(\theta)$ is a regularization term.

Computational complexity:

$$Q=N\times D+N\times D\times H + H\times V$$

Here we should have a rough estimation about the scale of each number:

N: 5 ~ 10
D: 500 ~ 2000
H: 500 ~ 1000
V: usually millions

It looks like that the dominator of $Q$ should be $H\times V$, however, a hierarchical softmax method can reduce $V$ to ideally $log_2(V)$. Then the dominant will become $N\times D\times H$.

This method is slow for the existance of the non-linear hidden layer. In 2013, Mikolov et al. showed that the hidden layer is not necessary and provided another model called Word2vec.

Word2vec

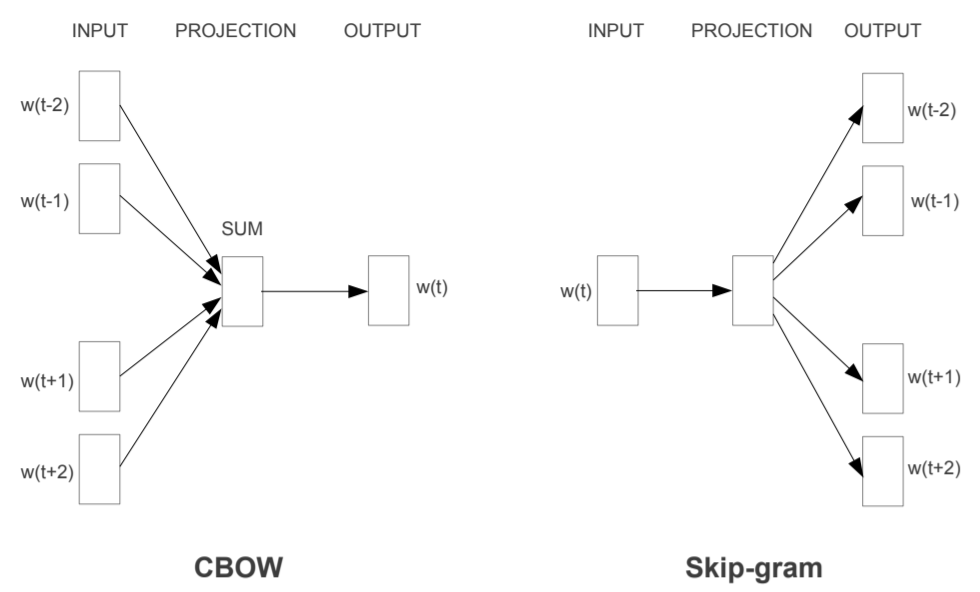
The method has two distinct model: CBOW and skip-gram. They share common idea that we don't need a extra hidden layer, but use the word vector to do prediction directly.

Objective function

The objective is mostly the same as NNLM. Note a difference that NNLM predict a word $w_t$ using its previous words, while the CBOW model predict word $w_t$ using both previous words and subsequent words.

continuous bag-of-words (CBOW)

• bag-of-words

  • any word is represented as a ont-hot vector with $V$ dimensions
  • a sentence, or a sequence of words is represented as the sum of words included
    

• continuous bag-of-words

  • any word is represented as a continuous vector (distributed representation)
  • a sentence, or a sequence of words is represented as the sum of words included

• computational complexity
  

  $$Q=N \times D+D \times \log _{2}(V)$$
  compare with it in NNLM, the dominating term $N \times D \times H$ disappeared because Word2vec removed the hidden layer.

• CBOW model works better in smaller scaled data.

skip-gram

• predict context words using only one word
• according to the distance to the input word, the output word in weighted through biased resampling
• computational complexity
  $$Q=C \times\left(D+D \times \log _{2}(V)\right)$$
  did not understand the $C\times D$ part
• works better in larger scaled data

---

tricks

hierarchical softmax

Use a Huffman tree to assign short binary codes to frequent words. The tree will be constructed as below:

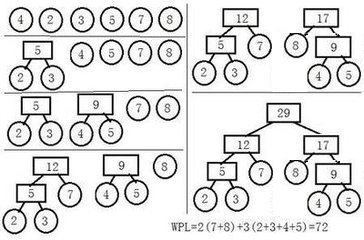
1. each node in the candidate pool is regard as a tree (with only root)
2. each tree has a score that to be minimized in the final tree
3. until converge:
    3.1 merge two trees in the candidate pool with the smallest scores
    3.2 add the new merging tree to the candidate pool, set its score as the sum of two merged tree
    3.3 removed the two merged tree from the candidate pool

negative sampling

phrase vector