[关闭]
@lzb1096101803 2016-03-08T12:58:45.000000Z 字数 7796 阅读 685

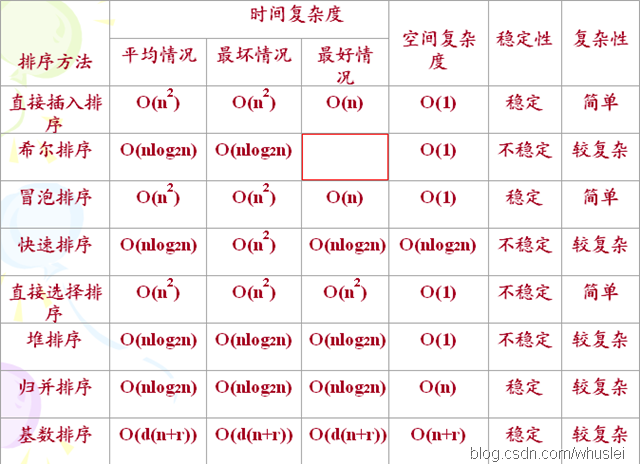
排序算法背诵

电话面试

冒泡排序

冒泡排序算法的运作如下：（从小到大）
- 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
- 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。结果，最后的元素应该会是最大的数。
- 针对所有的元素重复以上的步骤，除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较

  1. package 排序.冒泡排序;
  3. /**
  4.  * 冒泡排序
  5.  * 交换排序：冒泡排序和快速排序
  6.  * 最差O(n^2)  平均：O(n^2)  最好O(n)
  7.  * 空间复杂度：辅助存储O(1)
  8.  * 稳定
  9.  */
  10. public class BubbleSort {  
  13.     public void bubble(Integer[] data){ 
  15.         for(int i=0;i<data.length;i++){  
  16.             for(int j=0;j<data.length-1-i;j++){  
  17.                 if(data[j]>data[j+1]){   //如果后一个数小于前一个数交换  
  18.                     int tmp=data[j];  
  19.                     data[j]=data[j+1];  
  20.                     data[j+1]=tmp;  
  21.                 }  
  22.             }  
  23.         }  
  24.     }  
  25.     public static void main(String[] args) {  
  27.          Integer[] list={12,21,96,72,38,44,1};  
  28.          BubbleSort bs=new BubbleSort();  
  29.          bs.bubble(list);  
  31.          for(int i=0;i<list.length;i++){  
  32.              System.out.print(list[i]+" ");  
  33.          }  
  34.          System.out.println();  
  35.     }  
  36. }

选择排序

①初始状态：无序区为R[1..n]，有序区为空。
②第1趟排序
在无序区R[1..n]中选出关键字最小的记录R[k]，将它与无序区的第1个记录R[1]交换，使R[1..1]和R[2..n]分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区。

  1. package 排序.选择排序;
  3. /**
  4.  * 选择排序
  5.  * 最差O(n^2)  平均：O(n^2)  最好O(n^2)
  6.  * 空间复杂度：辅助存储O(1)
  7.  * 不稳定
  8.  */
  9. public class ChoseSort {  
  11.     public int[] choseSort(int[] intArr){  
  13.         for(int i=0;i<intArr.length;i++){  
  14.             int lowIndex = i;  
  15.             for(int j=i+1;j<intArr.length;j++){  
  16.                 if(intArr[j]>intArr[lowIndex]){  
  17.                     lowIndex = j;  
  18.                 }  
  19.             }  
  20.             //将当前第一个元素与它后面序列中的最小的一个 元素交换，也就是将最小的元素放在最前端
  21.             if(i!=lowIndex){
  22.                 int temp = intArr[i];             
  23.                 intArr[i] = intArr[lowIndex];  
  24.                 intArr[lowIndex] = temp;
  25.             }
  26.         }  
  28.         return intArr;  
  29.     }  
  31.     public static void main(String[] args) {  
  33.         ChoseSort choseSort = new ChoseSort();  
  34.         int[] intArr = {80,2,99,96,47,72,78};  
  35.         int[] intArrAfterSort = choseSort.choseSort(intArr);  
  36.         for(int k=0;k<intArrAfterSort.length;k++){
  37.             System.out.print(intArrAfterSort[k]+" ");
  39.         }
  40.     }
  41. }

插入排序

把待排序的纪录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的纪录插入完为止，得到一个新的有序序列。

  1. package 排序.简单插入排序;
  3. /**
  4.  * 简单插入排序
  5.  * 插入排序：简单插入排序和希尔排序
  6.  * 最差O(n^2)  平均：O(n^2)  最好O(n)   和冒泡一样
  7.  * 空间复杂度：辅助存储O(1)
  8.  * 稳定
  9.  */
  10. public class InsertSort {
  12.     public static void main(String[] args) {
  13.         int[] array = new int[] { 72,60,32,66,81,48,8 };
  14.         InsertSort.insertSort(array);
  16.          for(int k=0;k<array.length;k++){
  17.                System.out.print(array[k]+" ");
  18.          }
  19.     }
  21.     public static int[] insertSort(int[] arr) {
  22.         int i, j;
  23.         int insertNote;// 要插入的数据
  24.         int[] array = arr;
  26.         // 从数组的第二个元素开始循环将数组中的元素插入
  27.         for (i = 1; i < array.length; i++) {
  28.             // 设置数组中的第2个元素为第一次循环要播讲的数据
  29.             insertNote = array[i];
  30.             j = i - 1;
  31.             while (j >= 0 && insertNote > array[j]) {
  32.                 // 如果要播讲的元素小于第j个元素,就将第j个元素向后移动
  33.                 array[j + 1] = array[j];
  34.                 j--;
  35.             }
  36.             // 直到要插入的元素不小于第j个元素,将insertNote插入到数组中
  37.             array[j + 1] = insertNote;
  39.         }
  40.         // 打印排序后的数组
  41. //      System.out.println(Arrays.toString(array));
  42.         return array;
  44.     }
  45. }

快速排序

设要排序的数组是A[0]……A[N-1]，首先任意选取一个数据（通常选用数组的第一个数）作为关键数据，然后将所有比它小的数都放到它前面，所有比它大的数都放到它后面，这个过程称为一趟快速排序。值得注意的是，快速排序不是一种稳定的排序算法，也就是说，多个相同的值的相对位置也许会在算法结束时产生变动。

  1. package 排序.快速排序;
  3. /**
  4.  * 快速排序
  5.  * 交换排序：冒泡排序和快速排序
  6.  * 最差O(n^2)  平均：O(n*log2n)  最好O(n*log2n)
  7.  * 空间复杂度：辅助存储O(n*log2n)
  8.  * 不稳定
  9.  * 算法导论P95
  10.  * 分解-解决-合并
  11.  */
  12. public class QuickSort {
  14.      public static void main(String[] args) {  
  16.             Integer[] list={3,71,89,8,55,48,42};  
  18.              QuickSort.quickSort(list,0,list.length-1);  
  20.              for(int i=0;i<list.length;i++){  
  21.                  System.out.print(list[i]+" ");  
  22.              }  
  23.              System.out.println();  
  24.     }  
  26.     public static void quickSort(Integer[] list, int low, int high) {  
  28.         if (low < high) {  
  29.             int middle = getMiddle(list, low, high);  //将list数组进行一分为二 partition
  31.             for(int a:list){
  32.                 System.out.print(a+" ");
  33.             }   
  34.             System.out.println();
  35.             quickSort(list, low, middle - 1);        //对低字表进行递归排序  
  36.             quickSort(list, middle + 1, high);       //对高字表进行递归排序  
  37.         }  
  38.     }  
  40.     public static int getMiddle(Integer[] list, int low, int high) {  
  41.         int tmp = list[low];    //数组的第一个作为中轴  
  42.         while (low < high) {  
  43.             while (low < high && list[high] <= tmp) {  
  44.                 high--;  
  45.             }  
  46.           //比中轴小的记录移到低端  
  47.             if (low < high)
  48.                 list[low++] = list[high];
  49.             while (low < high && list[low] >= tmp) {  
  50.                 low++;  
  51.             }  
  52.     //比中轴大的记录移到高端
  53.             if (low < high)
  54.                 list[high--] = list[low];
  55.         }  
  56.         list[low] = tmp;              //中轴记录到尾  
  57.         return low;                   //返回中轴的位置  
  58.     }  
  61. }

归并排序

归并过程为：比较a[i]和a[j]的大小，若a[i]≤a[j]，则将第一个有序表中的元素a[i]复制到r[k]中，并令i和k分别加上1；否则将第二个有序表中的元素a[j]复制到r[k]中，并令j和k分别加上1，如此循环下去，直到其中一个有序表取完，然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元

  1. package 排序.归并排序;
  3. /**
  4.  * 归并排序
  5.  * 最差O(n*log2n)  平均：O(n*log2n)  最好O(n*log2n)
  6.  * 空间复杂度：辅助存储O(1)
  7.  * 稳定
  8.  */
  9. public class MergeSort {  
  11.     public static void main(String[] args) {  
  13.         int[] data = new int[] {59,93,99,0,95,1,46};  
  14.         print(data);  
  15.         mergeSort(data);  
  16.         System.out.println("排序后的数组：");  
  17.         print(data);  
  18.     }  
  20.     public static void mergeSort(int[] data) {  
  21.         sort(data, 0, data.length - 1);  
  22.     }  
  24.     public static void sort(int[] data, int left, int right) {  
  26.         if (left >= right)  
  27.             return;  
  28.         // 找出中间索引  
  29.         int center = (left + right) / 2;  
  30.         // 对左边数组进行递归  
  31.         sort(data, left, center);  
  33.         // 对右边数组进行递归  
  34.         sort(data, center + 1, right);  
  36.         // 合并  
  37.         merge(data, left, center, right);  
  38.         print(data);  
  39.     }  
  41.     /** 
  42.      * 将两个数组进行归并，归并前面2个数组已有序，归并后依然有序 
  43.      *  
  44.      * @param data 
  45.      *            数组对象 
  46.      * @param left 
  47.      *            左数组的第一个元素的索引 
  48.      * @param center 
  49.      *            左数组的最后一个元素的索引，center+1是右数组第一个元素的索引 
  50.      * @param right 
  51.      *            右数组最后一个元素的索引 
  52.      */  
  53.     public static void merge(int[] data, int left, int center, int right) {  
  54.         System.out.println();
  55.         System.out.println("left:"+left+" center"+center+" right:"+right);
  56.         // 临时数组  
  57.         int[] tmpArr = new int[data.length];  
  58.         // 右数组第一个元素索引  
  59.         int mid = center + 1;  
  60.         // third 记录临时数组的索引  
  61.         int third = left;  
  62.         // 缓存左数组第一个元素的索引  
  63.         int tmp = left;  
  64.         while (left <= center && mid <= right) {  
  66.             // 从两个数组中取出最小的放入临时数组  
  67.             if (data[left] >= data[mid]) {  
  68.                 tmpArr[third++] = data[left++];  
  69.             } else {  
  70.                 tmpArr[third++] = data[mid++];  
  71.             }  
  72.         } 
  73.         // 剩余部分依次放入临时数组（实际上两个while只会执行其中一个）  
  74.         while (mid <= right) {  
  75.             tmpArr[third++] = data[mid++];  
  76.         }  
  77.         while (left <= center) {  
  78.             tmpArr[third++] = data[left++];  
  79.         }  
  80.         // 将临时数组中的内容拷贝回原数组中  
  81.         // （原left-right范围的内容被复制回原数组）  
  82.         while (tmp <= right) {  
  83.             data[tmp] = tmpArr[tmp++];  
  84.         }  
  85.     }  
  87.     public static void print(int[] data) {  
  88.         for (int i = 0; i < data.length; i++) {  
  89.             System.out.print(data[i] + ",");  
  90.         }  
  91.         System.out.println();  
  92.     }  
  94. }

堆排序

堆排序利用了大根堆（或小根堆）堆顶记录的关键字最大（或最小）这一特征，使得在当前无序区中选取最大（或最小）关键字的记录变得简单。

构造大顶堆，堆排序

  1. package 排序.堆排序;
  3. /**
  4.  * 堆排序
  5.  * http://upload.wikimedia.org/wikipedia/commons/4/4d/Heapsort-example.gif
  6.  * 最差O(n*log2n)  平均：O(n*log2n)  最好O(n*log2n)
  7.  * 算法导论P84
  8.  */
  9. public class HeapSort {
  11.     public static void main(String[] args) {
  13.         int[] data = new int[]{16,4,10,14,28,9,3,2,8,30};
  14.         sort(data);
  15.         for(int a:data){
  16.             System.out.print(a+" ");
  17.         }
  18.     }
  20.     public static void sort(int[] data) {
  21.         // 构建最大堆
  22.         buildMaxHeap(data);
  24.         // 循环，每次把根节点和最后一个节点调换位置
  25.         for (int i = data.length; i > 1; i--) {
  26.             int tmp = data[0];
  27.             data[0] = data[i - 1];
  28.             data[i - 1] = tmp;
  29.             // 堆的长度减少1，排除置换到最后位置的根节点
  30.             maxHeapify(data, 1, i - 1);
  31.         }
  32.     }
  34.     // 根据输入数组构建一个最大堆                   i>heapSize/2都是叶子节点(下标从1开始)
  35.     private static void buildMaxHeap(int[] data) {
  36.         for (int i = (data.length) / 2; i > 0; i--) { 
  37.             maxHeapify(data, i, data.length);
  38.         }
  39.     }
  41.     //堆调整，以parentNodeIndex-1为根节点，使其子树生成最大堆
  42.     //parentNodeIndex最小只能是1，否则根节点得不到左右节点，因此下面采用parentNodeIndex-1获取值
  43.     private static void maxHeapify(int[] data, int parentNodeIndex, int heapSize) {
  44.         // 左子节点索引
  45.         int leftChildNodeIndex = parentNodeIndex * 2;
  46.         // 右子   索引
  47.         int rightChildNodeIndexAddOne = parentNodeIndex * 2 + 1;
  48.         // 最大节点索引
  49.         int largestNodeIndex = parentNodeIndex;
  51.         // 如果左子节点大于父节点，则将左子节点作为最大节点
  52.         //前面判断用于第一次时为了防止越界，&&具有截断作用
  53.         if (leftChildNodeIndex <= heapSize && (data[leftChildNodeIndex - 1] - data[parentNodeIndex - 1]) > 0) {
  54.             largestNodeIndex = leftChildNodeIndex;
  55.         }
  57.         // 如果右子节点比最大节点还大，那么最大节点应该是右子节点
  58.         if (rightChildNodeIndexAddOne <= heapSize && (data[rightChildNodeIndexAddOne - 1] - data[largestNodeIndex - 1]) > 0) {
  59.             largestNodeIndex = rightChildNodeIndexAddOne;
  60.         }
  62.         // 最后，如果最大节点和父节点不一致，则交换他们的值
  63.         if (largestNodeIndex != parentNodeIndex) {
  64.             int tmp = data[parentNodeIndex - 1];
  65.             data[parentNodeIndex - 1] = data[largestNodeIndex - 1];
  66.             data[largestNodeIndex - 1] = tmp;
  68.             // 交换完父节点和子节点的值，对换了值的子节点检查是否符合最大堆的特性
  69.             maxHeapify(data, largestNodeIndex, heapSize);
  70.         }
  71.     }
  73. }

基数排序

将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。

  2. package 排序.基数排序;
  4. import java.util.Arrays;
  6. /**
  7.  * 基数排序
  8.  * 最差O(d(n+r))  平均：O(d(r+n))  最好O(d(n+rd))
  9.  * 空间复杂度：辅助存储O(rd+n)
  10.  * 稳定
  11.  */
  12. public class RadixSort {
  15.      private static void radixSort(int[] array, int distance){
  17.          radixSort(array, 10, distance);
  18.      }
  19.      //基于计数排序的基数排序算法  
  20.     private static void radixSort(int[] array,int radix, int distance) {  
  21.         //array为待排序数组  
  22.         //radix，代表基数  
  23.         //distance代表排序元素的位数  
  25.         int length = array.length;  
  26.         int[] temp = new int[length];//用于暂存元素  
  27.         int[] count = new int[radix];//用于计数排序  每个位的个数有多少个，
  28.         int divide = 1;  
  30.         for (int i = 0; i < distance; i++) {  
  32.             System.arraycopy(array, 0,temp, 0, length);  
  33.             Arrays.fill(count, 0);  //每一次循环count数组清0
  35.             for (int j = 0; j < length; j++) {  
  36.                 int tempKey = (temp[j]/divide)%radix;  
  37.                 count[tempKey]++;  
  38.             }  
  40.             for (int j = 1; j < radix; j++) {  //记录每位个数后，作用改变了，变成要插入的位置
  41.                 count [j] = count[j] + count[j-1];  
  42.             }  
  44.             for (int j = length - 1; j >= 0; j--) {  
  46.                 int tempKey = (temp[j]/divide)%radix;  
  47.                 count[tempKey]--;  
  48.                 array[count[tempKey]] = temp[j];  
  49.             }  
  50.             for (int k = 0; k < array.length; k++) {  
  51.                 System.out.print(array[k]+" ");  
  52.             }  
  53.             System.out.println();
  54.             divide = divide * radix;                  
  56.         }  
  57.     }  
  59.     public static void main(String[] args) {  
  61.         int[] array = {27,55,58,94,77,46,13};  
  62.         radixSort(array,2);  //基数一般都是10
  63.         for (int i = 0; i < array.length; i++) {  
  64.             System.out.print(array[i]+" ");  
  65.         }  
  66.         System.out.println();
  67. /*        int[] array2 = {10,1001,1110,10000,1011011,0,101111};
  68.         radixSort(array2, 2, 6);
  69.         for (int i = 0; i < array2.length; i++) {  
  70.             System.out.print(array2[i]+" ");  
  71.         }*/  
  72.     }
  73. }
添加新批注
在作者公开此批注前，只有你和作者可见。
回复批注