如果准确度为99%的准确性测试结果为阳性，你会变成僵尸吗？——关于贝叶斯思维的介绍

未分类

总结一下这个问题：假设世界上存在一种罕见的僵尸病毒，只有1/1000的几率你会感染，你想知道你会不会染病，于是你做了一次准确度为99%的测试，结果是阳性的！这个时候，你能多确定你真的被感染了？
第二次测试又是如何影响你对感染的相信程度的？
你不想做这些数学计算，更想通过画画线图来更好的理解推广这个问题？

第一次测试
由于它是一种非常罕见的病毒（千分之一的感染率）。你体内有病毒的可能性由下表给出（下表被称作条件概率表）：

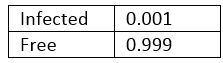
病毒感染率的条件概率表
上表说明只有1/1000的人感染了病毒。同样的说法是，999/1000的人没有被感染。
现在我们为了测试做个相似的表格：第二张表格表现了测试的准确性，也即测试表现真相的能力。所以，如果你感染了，测试结果有99%的可能是「真」；如果你并未感染，测试结果会是「假」（同样是99%的可能）。在两种情况下，误差率都为1%。

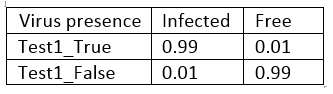
测试1的条件概率表
下图表明，当给定了测试结果，病毒是否存在基于测试（该图和上表相关联）。

一个简单的空的贝叶斯网络
之后，我给出测试结果为「真」的实例。贝叶斯网络表明，在一次测试中，测试结果表明病毒在你的体内，但是结果为阳性的概率只有9%！

加载了一次阳性测试结果的同一个贝叶斯网络
为什么呢？图中的结果来自于贝叶斯公式：

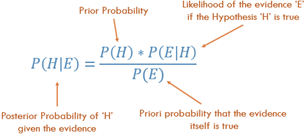
在这个问题里：
𝑃(H|E) = 𝑃(H) × 𝑃(E|H) / 𝑃(E)
𝑃(H|E) = 𝑃(H) × P(E|H) / (𝑃(E|H) × 𝑃(H) + 𝑃(E|Hc) × 𝑃(Ec) )
𝑃(H|E) = 0,99*0,001 / (0,001*0,99 + 0,999*0,01) = 0,9 = 9%
所以，即使你做了99%准确性的测试，你感染了僵尸病毒的概率也只有9%。
计算看上去挺复杂，但是一旦用图形来表现，我们就会在理解贝叶斯思维上有更好的直觉。
**两步测试
如果你接受第二次测试会怎样呢？让我们假定新的测试同样具有99%的准确率。和第一次测试一样，我们会得到一张表：

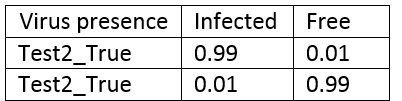
测试2的条件概率表
相符的贝叶斯网络如下所示：

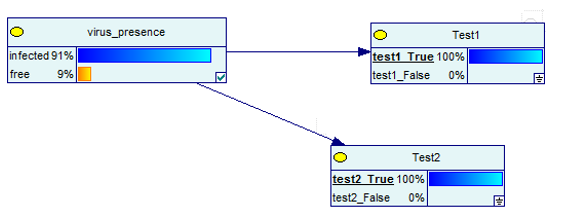
双阳测试的贝叶斯网络

这意味着，对于两个阳性测试而言，感染疾病的可能性上升到了91%！相对于先前的单次测试效果提升显著，有病的概率从9%变成了91%！即使这样，依然不是100%！
但是，如果第二次测试是阴性的，那么没有感染的概率是100%

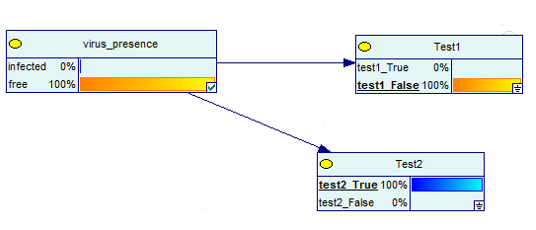
阳性测试+阴性测试的贝叶斯网络
三次测试
在同样准确率的三次测试中，我们看到了一些有趣的结果。如果三次测试的结果都是阳性的，现在，100%确定你已经被病毒感染啦！
在这种情况下，我为你感到遗憾：

但是如果其中一个测试结果为假，结果就转变了——只有91%的概率病毒存在于你的身体里。

总结一下，贝叶斯网络帮助我们理解贝叶斯思维。在数据科学中，如果模型的数据量中等，数据不完整或者可靠性存疑，这种思想就能派上用场。这个思想也可以用专业判断来建立或优化模型。它允许去「模拟」不同的场景。它表明输入值（在本文中是测试中病毒的存在与否和测试的准确性）是如何与输出（实际上具有疾病的概率）的置信水平挂钩的。
在这篇文章里我阐述了如何根据贝叶斯理论去构建贝叶斯网络。我目前正在基于贝叶斯网络来预测项目的成本和风险，我想分享一下这个能力爆表的AI工具的基础架构。
在这个视频里也解释了这个例子：https://youtu.be/R13BD8qKeTg
如果你想知道更多关于贝叶斯网络的知识：
关于模型源轴上的理论与数据之间的横向划分，贝叶斯网络有一个特殊的特征。贝叶斯网络可由人类的知识构建，例如基于理论，但也可以是由来源于数据的机器学习。因此，贝叶斯网络可以使用整个频谱（见下图）作为模型来源。同样的，由于它们的图形结构，机器学习得到的贝叶斯网络是可以作可视化说明的，因此促进了人类的学习和理论的构建。

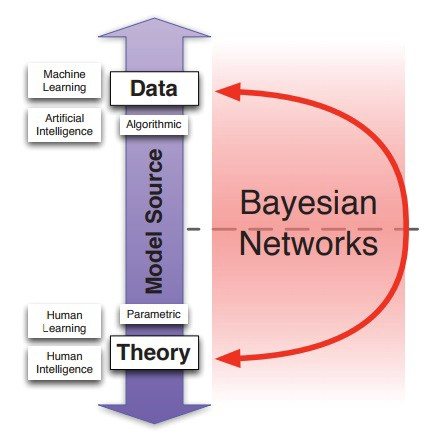
贝叶斯网络允许人类学习和机器学习一起工作，比如贝叶斯网络可以从人类智慧和人工智能的合作中发展出来。除了超越了理论和数据的边界，贝叶斯网络还具有因果关系的特殊性质。
在一定的条件下，通过具体的理论驱动假设，贝叶斯网络促进了因果推理。事实上，贝叶斯网络模型可以涵盖从关联/相关到因果关系的整个范围。
实际上，这意味着我们可以将因果假设添加到现有的非因果网络中，从而创建一个因果贝叶斯网络。当我们试图模拟一个领域的干涉条件时，这个特别重要，例如估计治疗的效果。在这种情况下，建立一个因果模型是必要的，而贝叶斯网络可以帮助我们实现这一转变。 来源：贝叶斯书