通过神经网络进行时序预测与建模（基础应用四）

matlab

---

动态网络是非常擅长进行时序预测的。
假设一个例子，你有一组酸碱度中和实验的数据。你想设计一个网络能预测水槽中酸碱度与基于流量的的酸度预测。你有2001个时间点的序列。

定义问题

定义一个时序问题，指定一个$TS$长度的输入向量为一列在一个cell数组中。然后指定$TS$长的目标向量（每个输出对应一个输入）到第二个cell数组（参加理解神经网络工具箱的数据结构）但是有情况你仅需要定义目标数据集合，例如你定义了一个时序问题，你想使用上一次序列作为预测下一次的输入。

targets = {1 2 3 4 5};

三种类型的选择

这里可以使用不同类型时序网络解决不同类型的问题。
以下是ntstool的界面。表示了三种类型。

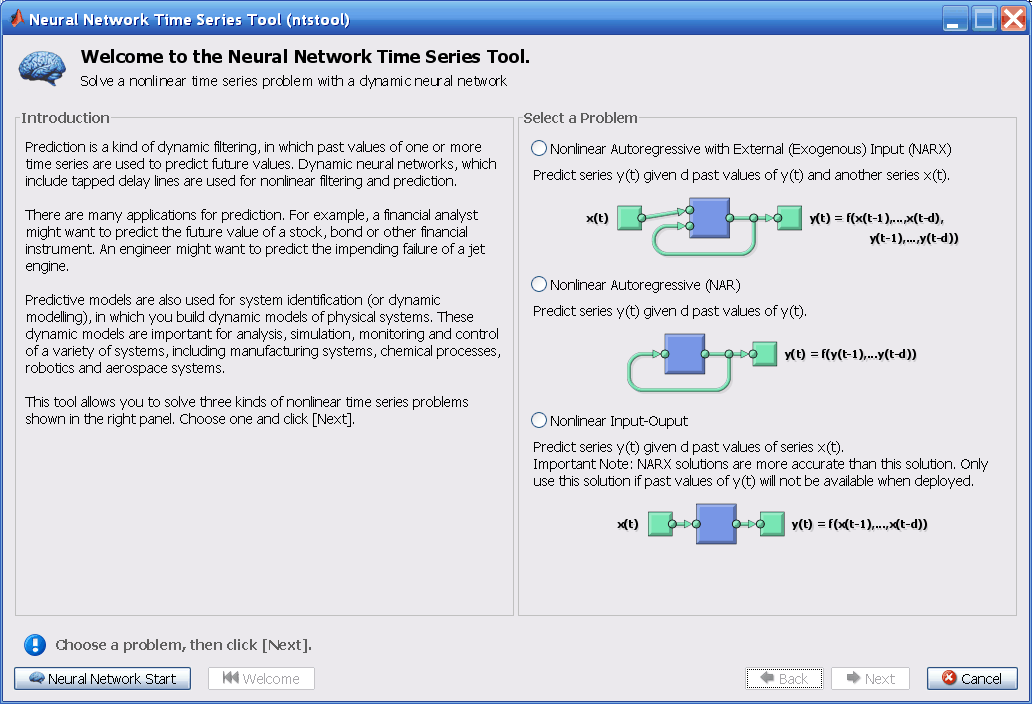
1. 第一种问题，你想预测未来在时间序$y(t)$的值。它的值依赖于当前的时间序$x(t)$以及过去时间点网络的输出。这种形式的预测被称为外部输入的非线性自回归，或者NARX网络。

$$y(t)=f(y(t-1),\ldots,y(t-d),x(t-1),\ldots,(t-d))$$ 模型可以预测股票于债卷，基于经济上的变量例如：失业率，GDP，等等。
2. 第二种类型是，仅有一个序列被提供。未来的时间点的值$y(t)$被预测仅依靠过去的序列。这种形式被称为非线性自回归也成为NAR。 $$y(t)=f(y(t-1),\ldots,y(t-d))$$ 模型被使用预测金融的工具。
3. 第三种类型类似第一种，两种序列被包含，一个输入序列$x(t)$与一个输入/目标序列$y(t)$。预测$y(t)$依据之前的$x(t)$，但是没有上一次的$y(t)$更多的信息。可以被写为： $$y(t)=f(x(t-1),\ldots,x(t-d))$$ NARX模型可以提供比这种input-output模型更好的预测。但是在有些应用方面上一个$y(t)$并没有什么用。在这种情况下使用这种模型替代NARX

NARX简单介绍

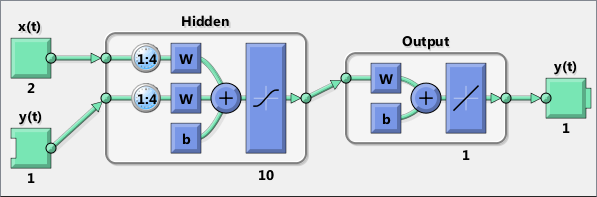
标准的NARX网络是一个两层前馈网络，隐藏层使用sigmoid激励函数，而输出层使用线性函数。这个网络使用一个延迟值来保存上一个时间点的$x(t)$与$y(t)$。网络的输出$y(t)$需要反馈回网络作为输入的一部分（通过延迟值），而$y(t)=f(y(t-1),\ldots,y(t-d),x(t-1),\ldots,(t-d))$。详细探讨参见NARX一文。

默认情况下隐藏层的神经元数被设置为$10$。默认延迟数量为$2$。

选择训练算法

默认Levenberg-Marquardt(trainlm)是被推荐的。但是对于一些噪声过大的问题贝叶斯正则化(trainbr)可以获取更好的结果但是消耗时间会更长。对于一些大型问题Scaled Conjugate Gradient(trainscg)被推荐使用但是它比其余两种算法花费的内存更多。

代码

% Solve an Autoregression Problem with External 
% Input with a NARX Neural Network
% Script generated by NTSTOOL
%
% This script assumes the variables on the right of 
% these equalities are defined:
%
%   phInputs - input time series.
%   phTargets - feedback time series.
inputSeries = phInputs;
targetSeries = phTargets;
% 创建外部输入的非线性自回归网络
inputDelays = 1:4;      % 输入延迟值
feedbackDelays = 1:4;   % 反馈延迟值
hiddenLayerSize = 10;   % 隐藏层数量
% 创建一个narx网络
net = narxnet(inputDelays,feedbackDelays,hiddenLayerSize);
% 为训练与仿真准备数据，函数PREPARETS为
% 指定的网络准备时序数据，改变时间的最小值
% 填充输入状态以及层状态。
% 使用PREPARETS允许你保持你的原始时序数据不改变
% 提早配置它来适应不同的数量的延迟值，在打开循
% 环与关闭循环反馈模式下
[inputs,inputStates,layerStates,targets] = ... 
    preparets(net,inputSeries,{},targetSeries);
% 设置数据集
net.divideParam.trainRatio = 70/100;
net.divideParam.valRatio = 15/100;
net.divideParam.testRatio = 15/100;
% 训练网络
[net,tr] = train(net,inputs,targets,inputStates,layerStates);
% 测试网络
outputs = net(inputs,inputStates,layerStates);
errors = gsubtract(targets,outputs);
performance = perform(net,targets,outputs)
% 浏览网络
view(net)
% 绘图
% Uncomment these lines to enable various plots.
% figure, plotperform(tr)
% figure, plottrainstate(tr)
% figure, plotregression(targets,outputs)
% figure, plotresponse(targets,outputs)
% figure, ploterrcorr(errors)
% figure, plotinerrcorr(inputs,errors)
% 关闭循环网络
% 使用这个网络做多步的预测。
% 函数CLOSELOOP直接替代从输出到输入的反馈
netc = closeloop(net);
netc.name = [net.name ' - Closed Loop'];
view(netc)
[xc,xic,aic,tc] = preparets(netc,inputSeries,{},targetSeries);
yc = netc(xc,xic,aic);
closedLoopPerformance = perform(netc,tc,yc)
% 早期预测网络
% 对于一些应用提高预测时间序。
% 例如市场决策一旦网络预测了y(t)，接下来就必须
% 得到y(t+1)的值
% 网络可以返回输出更早，通过移除延迟值，设定它的
% 值为0，替代原来的1。
% 这样新的网络将于原来一样返回输出但是比原来早
% 先一个时间点。
nets = removedelay(net);
% 预测前一个时间点
nets.name = [net.name ' - Predict One Step Ahead'];
view(nets)
[xs,xis,ais,ts] = preparets(nets,inputSeries,{},targetSeries);
ys = nets(xs,xis,ais);
earlyPredictPerformance = perform(nets,ts,ys)

创建一个NARX网络，使用narxnet，这是一个前向两层的网络，隐藏使用sigmod激励函数，输出层采用线性函数。有两个输入，一个是外部的输入，另外一个接收从网络输出反馈。（在网络训练完成之后，网络反馈链接可以被关闭）。对于每个输入，都有一个延迟线保存上一个的值。对一个网络指定结构，你必须选择与每个延迟线关联的延迟与隐藏层的神经元数量。下面的代码。指定了输入延迟与反馈延迟的范围以及隐藏层神经元的数量。

inputDelays = 1:4;
feedbackDelays = 1:4;
hiddenLayerSize = 10;
net = narxnet(inputDelays,feedbackDelays,hiddenLayerSize);

增加延迟与神经元的数量会加大计算量，如果值太大还会引起过拟合现象，但是可以解决更复杂的问题。

准备寻得数据，当一个网络包含延迟线时，填充输入与输出的初始值以及延迟的初始值。通过函数preparets。这个函数有三个输入参数：网络，输入序列与目标序列。函数返回需要填充延迟线的初始条件，并且修改输入与输出序列。

[inputs,inputStates,layerStates,targets] = ...
    preparets(net,inputSeries,{},targetSeries);

可以在NARX网络在打开状态时关闭循环状态。当循环关闭时可以在$y(t),x(t)$下预测$y(t+1)$。下面就是关闭网络循环的命令。

netc = closeloop(net);
netc.name = [net.name ' - Closed Loop'];
view(netc)
[xc,xic,aic,tc] = preparets(netc,inputSeries,{},targetSeries);
yc = netc(xc,xic,aic);
perfc = perform(netc,tc,yc)

从一个网络移除一个延迟，提前预测一个预测时期。

nets = removedelay(net);
nets.name = [net.name ' - Predict One Step Ahead'];
view(nets)
[xs,xis,ais,ts] = preparets(nets,inputSeries,{},targetSeries);
ys = nets(xs,xis,ais);
earlyPredictPerformance = perform(nets,ts,ys)

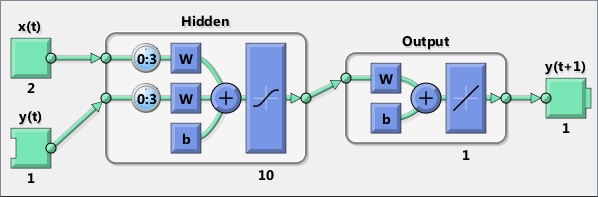
从图中可以看出提取了一个预测时间点。

如果你得到更好的结果，尝试以下的方式：
* 重新设置网络权重与偏置值使用init函数后再次训练网络
* 增加隐藏层的神经元
* 增加训练向量的数量
* 增加输入的有效特征的数量
* 尝试不同的训练算法（参见训练算法一文）

想要做更多的绘制图像可以使用plotroc与plottrainstate命令。

每次一个神经网络被训练完毕，结果都有所不同这是因为不同的初始化权值与偏置值与不同的训练，验证，测试的几何。不同的神经网络在同一问题同一输入上训练结果不同。

参见提高神经网络适应性与避免过拟合一文。

总结