二分查找

算法

二分查找法是对一组有序的数字中进行查找，传递相应的数据，进行比较查找到与原数据相同的数据，查找到了返回对应的数组下标，没有找到返回-1；

1、基本二分查找实现

1. while循环

   /**
    * 循环实现
    * @param array 已排序数组
    * @param target 目标
    * @return 找不到返回-1，找到返回下标
    */
   private static int binarySearch(int[] array, int target) {
       int low = 0;
       int high = array.length - 1;
       while (low <= high) {
           int mid = low + (high - low) / 2; //注意此处写法，避免越界
           if (array[mid] > target) {
               high = mid - 1;
           } else if (array[mid] < target) {
               low = mid + 1;
           } else {
               return mid;
           }
       }
       return -1;
   }

2. 递归实现

   private static int binarySearch(int[] array, int target, int low, int high) {
       int mid = low + (high - low) / 2;
       if (array[mid] == target) {
           return mid;
       }
       if (low >= high) {
           return -1;
       } else if (target > array[mid]) {
           return binarySearch(array, target, mid + 1, high);
       } else if (target < array[mid]) {
           return binarySearch(array, target, low, mid - 1);
       }
       return -1;
   }

2、变形

随着二分查找的进行，如果找到key并不结束循环的话，最终的结束状态会是right < left，并且right + 1 = left。

• 当数组中存在key时，根据二分区间选择的不同，这里又分为两种情况，如下图（key为2时）
• 当数组中不存在key时，最后仅有一种情况，即把图中的红色框框去掉。

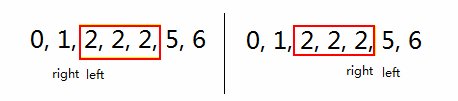
那么，可以找到：

1. 最后一个小于key的元素 1 左right
2. 第一个大于等于key的元素 2 左left
3. 最后一个小于等于key的元素 2 右right
4. 第一个大于key的元素 5 右left

另外，如果存在多个key时，稍加判断，就可以找到

1. 第一个与key相等的元素
2. 最后一个与key相等的元素

while (left <= right) {
    mid = (left + right) / 2;
    if (key ? arr[mid]) {
        right = mid - 1;
    } else {
        left = mid + 1;
    }
}
return ?;

根据要求的值的位置，先确定比较符号，再确定返回值，
比较符号：左<=，右<
返回值：左right，右left

2.1 查找最后一个小于key的元素

//1 查找最后一个小于key的元素
int findLastLess(int arr[], int len, int key) {
    int left = 0;
    int right = len - 1;
    int mid;
    while (left <= right) {
        mid = left + (right - left) / 2;
        if (key <= arr[mid]) {  // <=  意为左
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return right;     //返回左边值right
}

2.2 查找第一个大于等于key的元素

//2 查找第一个大于等于key的元素
int findLastLess(int arr[], int len, int key) {
    int left = 0;
    int right = len - 1;
    int mid;
    while (left <= right) {
        mid = left + (right - left) / 2;
        if (key <= arr[mid]) {  // <=  意为左
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return left;     //返回右边值left
}

2.3 查找最后一个小于等于key的元素

//3 查找第一个大于等于key的元素
int findLastLess(int arr[], int len, int key) {
    int left = 0;
    int right = len - 1;
    int mid;
    while (left <= right) {
        mid = left + (right - left) / 2;
        if (key < arr[mid]) {  // <=  意为右
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return right;     //返回左边值right
}

2.4 查找第一个大于key的元素

//4 查找第一个大于key的元素
int findLastLess(int arr[], int len, int key) {
    int left = 0;
    int right = len - 1;
    int mid;
    while (left <= right) {
        mid = left + (right - left) / 2;
        if (key < arr[mid]) {  // <=  意为右
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return left;     //返回右边值left
}

2.5 查找第一个与key相等的元素

//5 查找第一个与key相等的元素
int findFirstEqual(int arr[], int len, int key) {
    int left = 0;
    int right = len - 1;
    int mid;
    while (left <= right) {
        mid = left + (right - left) / 2;
        if (key <= arr[mid]) {  // <=  意为左
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    //right是最后一个小于key的
    //left是第一个大于等于key的
    if (left < len && arr[left] == key) {
        return left;
    }
    return -1;
}

2.6 查找最后一个与key相等的元素

//6 查找最后一个与key相等的元素
int findLastEqual(int arr[], int len, int key) {
    int left = 0;
    int right = len - 1;
    int mid;
    while (left <= right) {
        mid = left + (right - left) / 2;
        if (key < arr[mid]) {  // <  意为右
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    //right是最后一个小于key的
    //left是第一个大于等于key的
    if (right >= 0 && arr[right] == key) {
        return right;
    }
    return -1;
}

参考资料

你真的会写二分查找吗？-搏风雨