Homework 7

Haoming Jiang

8.1

$Y|m_k = (X\beta + \epsilon)|m_k \sim N(x\alpha,\sigma^2(XVX'+I))$
We have $\frac{v \lambda}{\sigma^2} \sim \chi^2(v)$,
$p(\sigma^2) = \frac{(v\lambda)^{v/2}}{2^{v/2}\Gamma(v/2)}(\frac{1}{\sigma^2})^{v/2+1}e^{-\frac{v\lambda}{2\sigma^2}}$
$p(y) = \int p(y|\sigma^2)p(\sigma^2) \\ = \int \frac{1}{(2\pi)^{n/2}|XVX'+I|^{1/2}} e^{-\frac{(Y-X\alpha)'(XVX'+I)^{-1}(Y-X\alpha)}{2\sigma^2}} \frac{(v\lambda)^{v/2}}{2^{v/2}\Gamma(v/2)}(\frac{1}{\sigma^2})^{v/2+1}e^{-\frac{v\lambda}{2\sigma^2}} d\sigma^2 \\ =\frac{\Gamma(\frac{v+n}{2}) (v\lambda)^{v/2}}{\pi ^ {n/2} \Gamma(v/2) |XVX'+I|^{1/2}}[v\lambda + (Y-X\alpha)'(XVX'+I)^{-1}(Y-X\alpha)]^{-\frac{n+v}{2}}$

8.3

a

$p(\theta|x) \propto p(x|\theta)p(\theta) \propto \theta^{x+\alpha-1}(1-\theta)^{n+\beta-x-1}$, which means $\theta|x \sim Beta(x+\alpha,n+\beta-x)$

b

$E(X) = E(E(X|\theta)) = E(n\theta)=n\frac{\alpha}{\alpha+\beta}$

c

n=10
a = 10
b = 5
rec = rep(0, 11)
for(i in 0:10){
  rec[i+1] = choose(n, i)*beta(a+i, b+n-i) / beta(a, b)
}
m = 100
theta = x = rep(0, m)
x[1] = 0
theta[1] = rbeta(1, a+x[1], b+n-x[1])
for(i in 2:m){
  x[i] = rbinom(1, n, prob = theta[i-1])
  theta[i] = rbeta(1, a+x[i-1], b+n-x[i-1])
}
plot(x, theta)

d

## d
q = function(x, u, v) qbinom(v, n, qbeta(u, a+x, b+n-x) )
ss = 0:10
start_times = c()
X0s = c()
for(i in 1:100)
{
a = 10
b = 5
n = 10
xx = ss
U = runif(2)
u = U[1]; v = U[2]
for(i in 1:(n+1)) xx[i] = q(ss[i], u, v)
while( length(table(xx)) != 1 ){
  U = rbind(U, runif(2))
  path = xx = ss
  for(tau in (dim(U)[1]:1) ){
    u = U[tau, 1]; v = U[tau, 2]
    for(i in 1:length(ss) ) xx[i] = q(xx[i], u, v)
    path = rbind(xx, path)
  }
  path
}
l = dim(path)[1]
plot( rep((-l:-1 +1), 11), rep(rep(0:10), each = l), cex = 0.3, xlab = "tau", ylab = "sample space" )
for(k in 1:11)  points((-l:-1 +1), rev(path[, k]), "l")
X0s = c(X0s, xx[1])
start_times = c(start_times,-l+1)
}
hist(start_times)
hist(X0s)

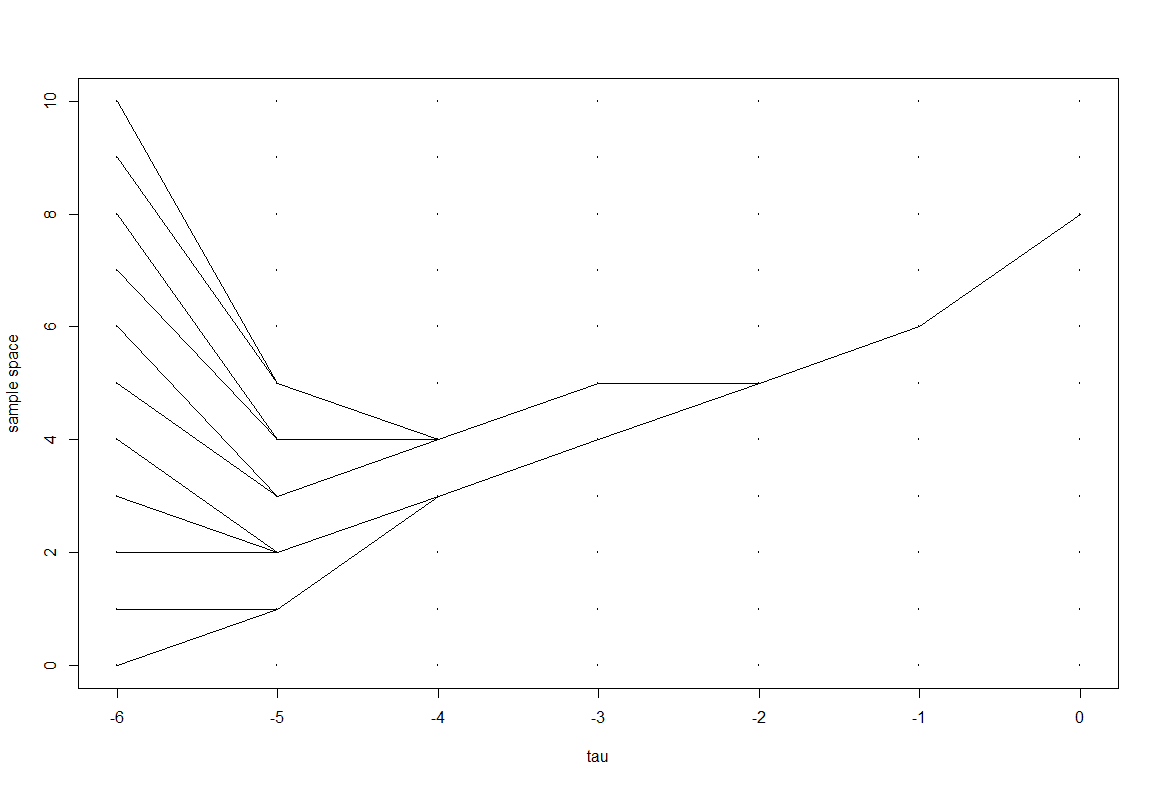
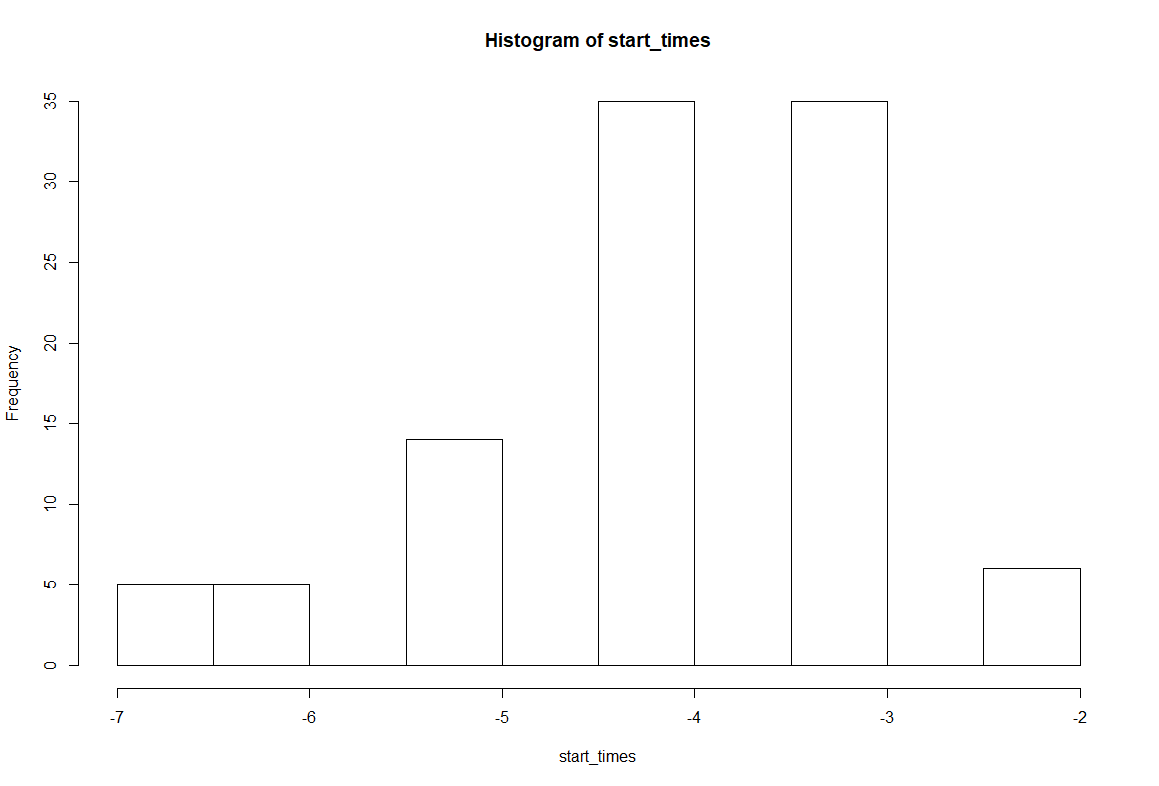
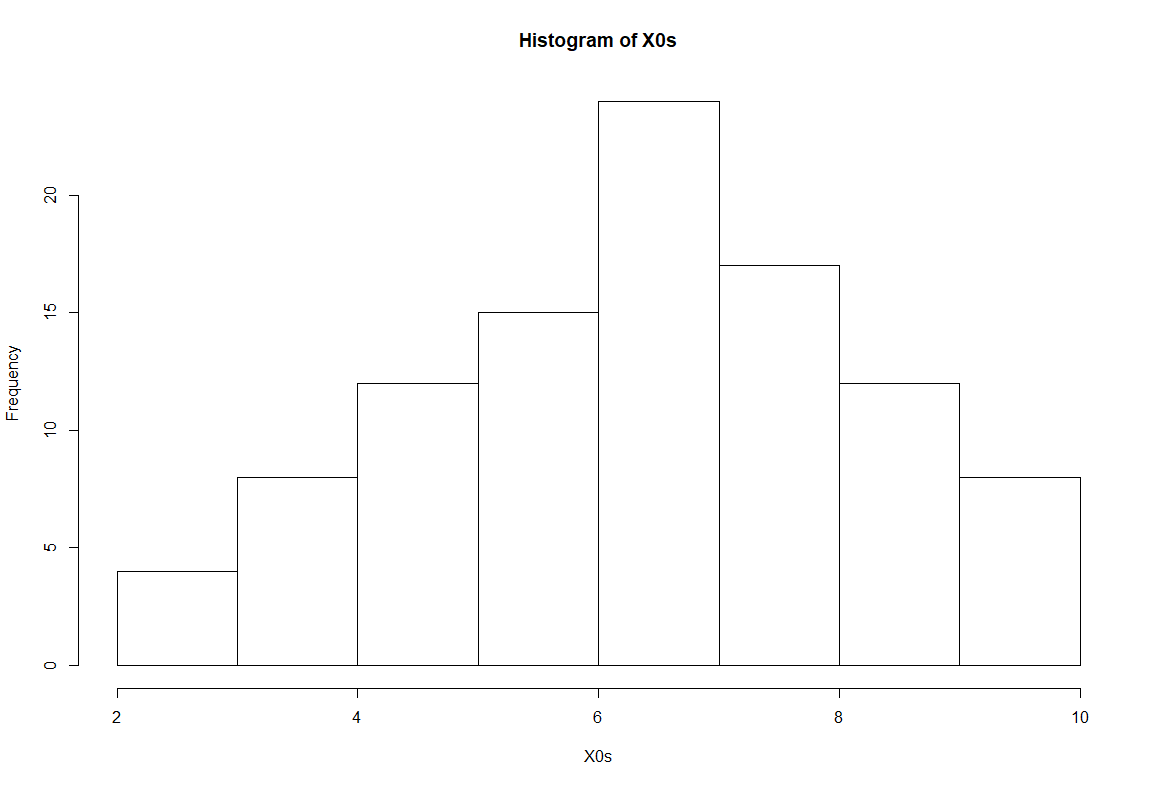
e

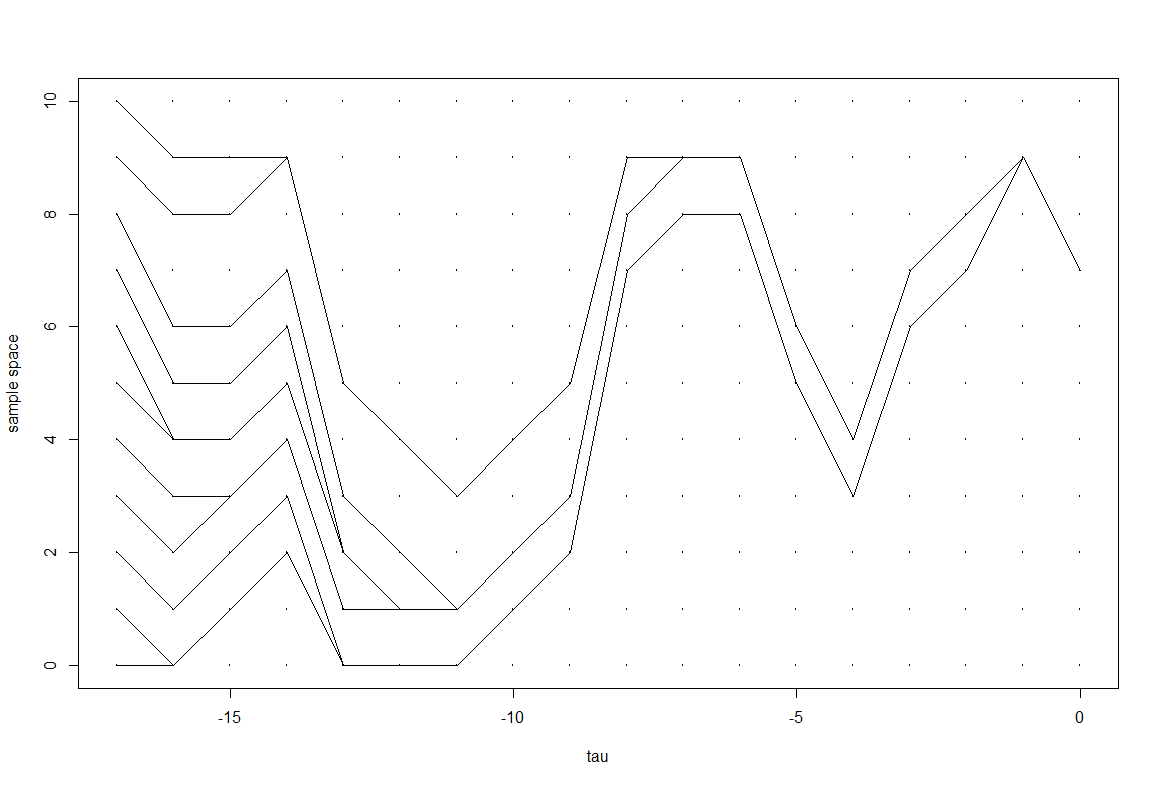
f

## f
a = 10
b = 5
n = 10
k=11
set.seed(k)
xx = ss
U = runif(2)
u = U[1]; v = U[2]
for(i in 1:(n+1)) xx[i] = q(ss[i], u, v)
while( length(table(xx)) != 1){
  U = rbind(U, runif(2))
  path = xx = ss
  for(tau in (dim(U)[1]:1) ){
    u = U[tau, 1]; v = U[tau, 2]
    for(i in 1:length(ss) ) xx[i] = q(xx[i], u, v)
    path = rbind(xx, path)
  }
  #path
}
#path
theta = gibbs = perfect = rep(0, 20)
gibbs[1] = perfect[1] = 0
theta[1] = rbeta(1, a+gibbs[1], b+n-gibbs[1])
for(i in 2:20){
  ## perfect
  u = runif(1); v = runif(1)
  perfect[i] = q(perfect[i-1], u, v)
  ## gibbs
  gibbs[i] = rbinom(1, n, prob = theta[i-1])
  theta[i] = rbeta(1, a+gibbs[i-1], b+n-gibbs[i-1])
}
plot(rep((0:19), 11), rep(rep(0:10), each = 20), cex = 0.3, xlab = "tau", ylab = "sample space" )
points(0:19, perfect, "l")
points(0:19, gibbs, lty = 2, "l")
legend("topleft", legend = c("CFTP", "Gibbs"), lty=1:2)

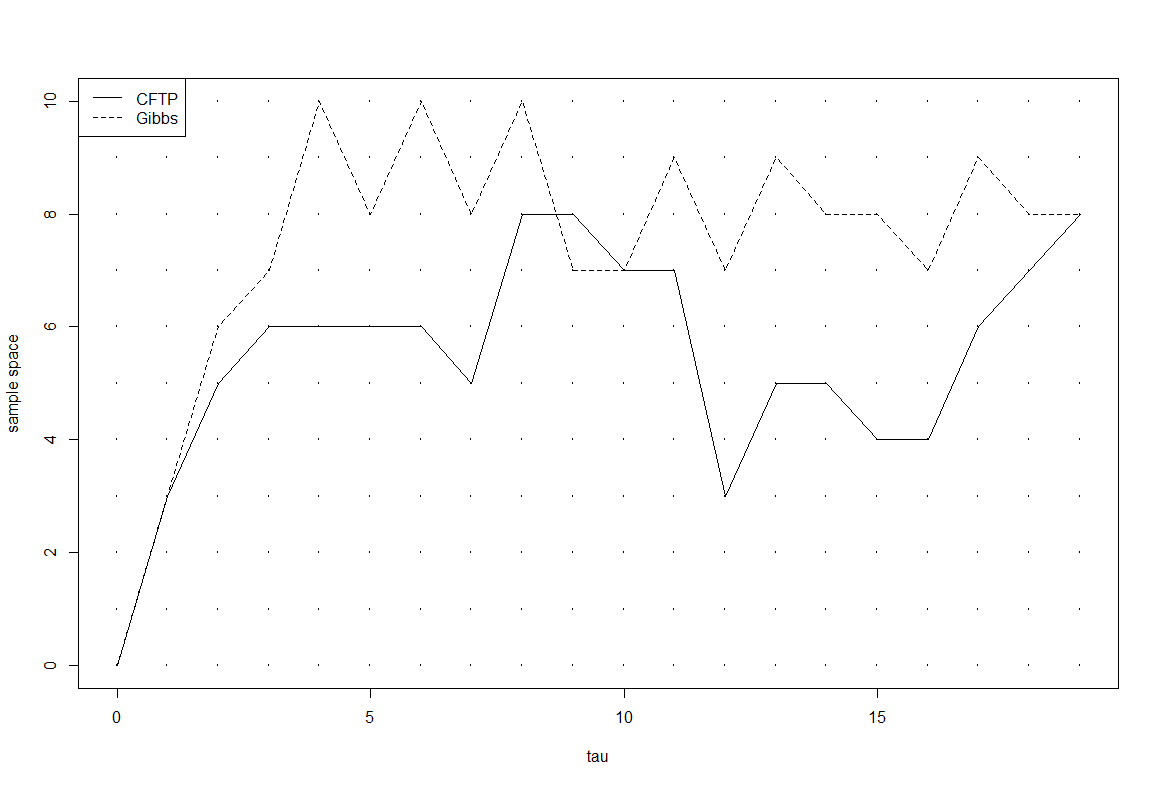
i Yes
ii CFTP