Active Defense-Based Resilient Sliding Mode Control Under Denial-of-Service Attacks

security
Wu C, Wu L, Liu J, et al. Active Defense-Based Resilient Sliding Mode Control Under Denial-of-Service Attacks[J]. IEEE Transactions on Information Forensics and Security, 2020, 15(1): 237-249.

2020-5-15

这篇，看错方向了。
本篇目的：针对网络物理系统的遭遇DoS攻击时的弹性控制问题提出用0和博弈来构建混合防御机制。

Introduction

对于CPS的攻击防御策略的工作有：【4-10】，本文提出如何建立在CPS被DoS攻击时的一种弹性控制架构。基于DoS攻击的的有效控制工作有【14-17】，针对于DoS攻击的博弈论防御策略工作有【20-27】。本文贡献：将物理过程表示成一个基于攻击频率和攻击持续时间的转换过程；使用滑动弹性转换模型使得当DoS攻击发生时物理过程仍然稳定；提出一个有效的防御策略控制转换逻辑。

System Formulation and Preliminaries

控制蓝图如图1。

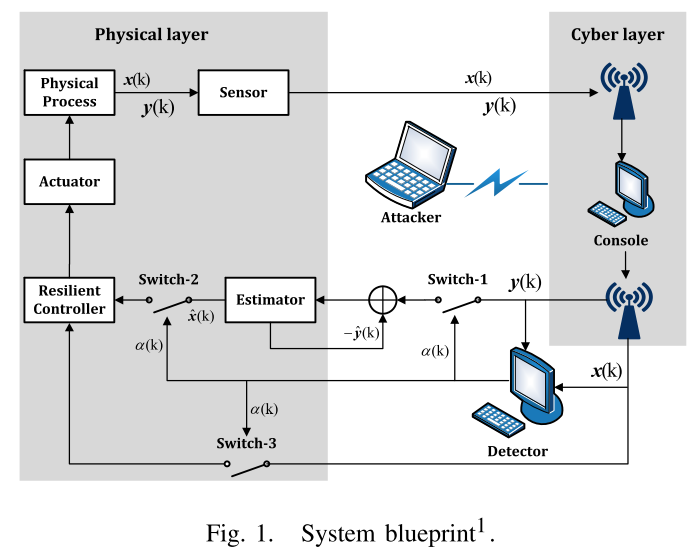
CPS由物理层和网络层组成，物理层有传感器和执行器，其估计器和弹性控制器可通过观测损失信号来保证DoS发生时物理过程能有可靠性能，检测器可以得知是否数据包被接收并基于此决定switch的状态。

A. Physical Proces Description

物理过程可由离散模型表示，如式（1）。
"$x ( k + 1 ) = A x ( k ) + B u ( k ) \tag{1}$"
$x(k) \in R^{nx},u(k) \in R^{nu}$分别表示状态向量和控制输入，测量输出表达为$y(k) = Cx(k)$，这里的A,B,C为相应的矩阵，B列满秩。本文这里考虑的均为线性物理过程。

B. DoS Attack

本文只考虑恶意传感DoS攻击，定义$K_j$为攻击发生的时间点，则第j个时间点攻击发生表示为："

$$T _ { j } \triangleq \{ k _ { j } \} \cup [ k _ { j } , k _ { j } + \tau _ { j } )$$ "，这里$\tau _j \ge 0$，其为持续时间。再定义：$\Gamma(\tau ,k),\Psi(\tau ,k)$分别为攻击发生和未发生的时间间隔，则有： $$\Gamma(\tau, k) \triangleq \bigcup _{j \in N} T_{j} \bigcap(\tau, k), \quad \Psi(\tau, k) \triangleq[\tau, k] \backslash \Gamma(\tau, k)$$ ,$|\Gamma(\tau ,k)|,|\Psi(\tau ,k)|$分别表示其长度。
假设1. 攻击频率：存在$\tau _D > 1$，有 $$n(\tau, k) \leq \frac{k-\tau}{\tau_{D}}$$
假设2. 攻击持续时间假设：存在$T_a > 1$，有：
$$|\Gamma(\tau, k)| \leq \frac{k-\tau}{T_{a}}$$
假设1类似平均持续时间，$n(\tau ,k)$为DoS攻击次数。

Resilient Sliding Mode Control Design

A. Estimator Design

估计器设计：为补充被攻击而损失的信号，估计器估计状态信号如式（2）。
$\hat{x}(k+1)=A \hat{x}(k)+B u(k)+L_{\alpha(k)} e_{D o S}(k) \tag{2}$
这里$\hat{x}(k)$为对x(k)的估计。"$L _ { \alpha } ( k )$"为switching的收益，$\alpha (k)$取{0，1}，分别表明在攻击情况和未攻击情况下的switching。$e_{DoS}(k) = \bar{y}(k) - \hat{y}(k)$，其中$\hat{y}(k)$为估计器的测量输出，$\hat{y}(k)=C \hat{x}(k)$。$\bar{y}(k)$取决于攻击是否发生，"$k \in \Gamma ( \tau , k ) , \overline { y } ( k ) = 0$"，"$k \in \Psi ( \tau , k ) , \overline { y } ( k ) = y ( k ) = C x ( k )$"。为简单表达，记$i = \alpha (k),L_i = L_{\alpha (k)}$

B. Sliding Mode Approach

滑动模型函数定义如式(3).
$s(k)=G_{i} \hat{x}(k)-G_{i}\left(A+B K_{i}\right) \hat{x}(k-1) \tag{3}$
$G_i,K_i$为矩阵，因此等价控制如式（4）。
$u_{e q}(k)=K_{i} \hat{x}(k)-\left(G_{i} B\right)^{-1} G_{i} L_{i} e_{D o S}(k) \tag{4}$
定义误差：$e(k) = x(k) - \hat{x}(k)$，则结合式（1，2，3）可得式（5）
$\xi(k+1)=\hat{A}_{i} \xi(k)+\hat{L}_{i} e_{D o S}(k) \tag{5}$
这里：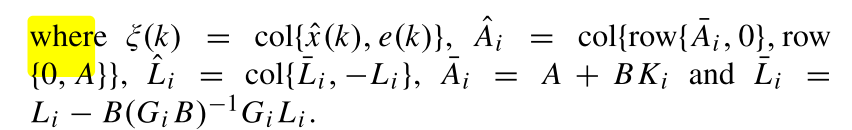
因此我们可以通过Lyapunv函数分析式（5）系统，定义：$V(\xi(k), \alpha(k))=\xi^{T}(k) P_{\alpha(k)} \xi(k)$为Lyapunov函数，其中$P_{\alpha}(\alpha (k) = 0,1)$为正定对称矩阵，分析过程如下三步：
step1:持续攻击情况$k \in \Gamma (0,k),\alpha(k) = i = 0$，则式（5）可写作

$$\xi ( k + 1 ) = \tilde { A } _ { 0 } \xi ( k )$$ ,其中"$\tilde { A } _ { 0 } = \operatorname { col } \{ \operatorname { row } \{ \overline { A } _ { 0 } - \overline { L } _ { 0 } C , 0 \} , \operatorname { row } \{ L _ { 0 } C , A \} \}$"，因此可得式（6）：
$\Delta V(\xi(k), \alpha(k))=\xi^{T}(k)\left(\tilde{A}_{0}^{T} P_{0} \tilde{A}_{0}-P_{0}\right) \xi(k) \tag{6}$
step2:无攻击情况$k \in \Psi (0,k),\alpha (k) = i = 1$,则有： $$\xi(k+1)=\tilde{A}_{1} \xi(k)$$
这里的$\tilde{A}_{1}=\operatorname{col}\left\{\operatorname{row}\left\{\bar{A}_{1}, \bar{L}_{1} C\right\}, \operatorname{row}\left\{0, A-L_{1} C\right\}\right\}$，可得式（7）：
$\Delta V(\xi(k), \alpha(k))=\xi^{T}(k)\left(\tilde{A}_{1}^{T} P_{1} \tilde{A}_{1}-P_{1}\right) \xi(k) \tag{7}$
step3: switching 情况发生在$k \in \Gamma (0,k)$和$k \in \Psi (0,k)$之间。此时为为保证过程的稳定性收益应有如下限制，如式（8）：
$\left. \begin{array} { l } { \tilde { A } _ { 0 } ^ { T } P _ { 0 } \tilde { A } _ { 0 } - P _ { 0 } < ( \overline { \alpha } - 1 ) P _ { 0 } } \\ { \tilde { A } _ { 1 } ^ { T } P _ { 1 } \tilde { A } _ { 1 } - P _ { 1 } < ( \frac { 1 } { \overline { \beta } } - 1 ) P _ { 1 } } \end{array} \right.\tag{8}$
这里的$\bar{\alpha},\bar{\beta}$为正标量，属于（1，无穷大).
定义$X_0 = P_0 ^{-1},X_1 = P_1 ^{-1}$，将schur complement应用到（8）中可得："$\Theta _ { 0 } < 0 , \Theta _ { 1 } < 0$"，这里$X_0 P_0 = I,X_1 P_1 = I$,"$\Theta _ { 0 } = \operatorname { col } \{ \operatorname { row } \{ - X _ { 0 } , \tilde { A } _ { 0 } \} , \operatorname { row } \{ \tilde { A } _ { 0 } ^ { T } , - \overline { \alpha } P _ { 0 } \} \}$","$\Theta _ { 1 } = \operatorname { col } \{ \operatorname { row } \{ - X _ { 1 } , \tilde { A } _ { 1 } \} , \operatorname { row } \{ \tilde { A } _ { 1 } ^ { T } , - \frac { 1 } { \beta } P _ { 1 } \} \}$".收益$K_i,L_i$的计算如算法1。

C. Stability Analysis

物理系统（1）遭受的DoS攻击满足假设1，2时，当给定$G_i,u > 1,\bar{\alpha},\bar{\beta} belong(1,\infty )$,若存在"$\hat { \varrho } > 1$",正定矩阵$P_i,X_i$和矩阵$L_i,K_i$使得算法1有可行解且满足：
"

$$\frac { \ln \mu } { \tau _ { D } } < \ln \hat { \varrho } , \quad \frac { \ln \overline { \beta } - \varphi \ln \hat { \varrho } } { \ln \overline { \alpha } + \ln \overline { \beta } } > \frac { 1 } { T _ { a } } , \quad P _ { i } \leq \mu P _ { j } , \quad i , j \in \{ 0,1 \}$$ "
则式(5)则可保证指数稳定，稳定率为"$\hat { \varrho } ^ { ( 2 - \varphi ) } ( \varphi > 2 )$"。

Resilient Sliding Mode Controller Design

滑动模型函数如式（3），则系统（1）的轨迹可通过如下控制来获得预测轨迹，控制如式（9）
$\begin{aligned} u(k)=& K_{i} \bar{x}(k)-\left(G_{i} B\right)^{-1}\left\|G_{i} L_{i} e_{D o S}(k)\right\| \operatorname{sign}(s(k)) \\ &-\left\|K_{i}(\bar{x}(k)-\hat{x}(k))\right\| \operatorname{sign}(s(k)) \\ &-\left(G_{i} B\right)^{-1} \Lambda s(k) \end{aligned} \tag{9}$
其中$\Lambda > 0$为调节矩阵，"$\overline { x } ( k ) = \left\{ \begin{array} { l l } { \hat { x } ( k ) , } & { k \in \Gamma ( 0 , k ) } \\ { x ( k ) , } & { k \in \Psi ( 0 , k ) } \end{array} \right.$"

• 下面例子不解释了,相当于实验总分，其通过实验证明算法一可使得在遭受攻击时能保证状态指数平滑。

Active Defense-Based Resilient Control

本部分通过博弈论找最优防御机制，为表示额外动荡衰减，这里将系统（1）重写为式(10):
"$x ( k + 1 ) = A x ( k ) + B u ( k ) + E \omega ( k ) \tag{10}$"
E为已知矩阵$\omega (k)$为额外衰减。攻击发生率定义为"$\frac { | \Gamma ( 0 , k ) | } { k - 0 }$"，其由博弈论决定。

A. Optimal Dfense Strategy

将防御和攻击方看作0和博弈的两方，最优防御策略可通过计算博弈矩阵获得。攻击者的攻击行为选自库:$\mathbb{A} - \left\{a_{1}, a_{2}, \ldots, a_{M}\right\}$，防御库为："$D = \{ d _ { 1 } , d _ { 2 } , \ldots , d _ { N } \}$"，定义$\bar{\mathbb{D}}$为防御库所有可的子集，并定义："$\overline { D } _ { m } \in \overline { D } , m \in \{ 1,2 , \ldots , 2 ^ { N } \}$"为防御者先择的策略。再定义：$f\left(\theta, \bar{D}_{m}\right)$ and $g\left(\theta, a_{n}\right)$为分别为攻击与防御在状态$\theta$选择相应策略的概率，$\theta \in \Theta$，$\Theta=\left\{\theta_{1}, \theta_{2}, \ldots \theta_{s}\right\} .0 \leq f\left(\theta, \bar{D}_{m}\right) \leq 1,0 \leq g\left(\theta, a_{n}\right) \leq 1$，$\sum_{m=1}^{2 N} f\left(\theta, \bar{D}_{m}\right)=1, \sum_{n=1}^{M} g\left(\theta, a_{n}\right)=1$。当前状态是否改变取决于双方的策略，本文使用马尔可夫链来表示$\theta$的改变，转换概率记为："$\operatorname { Prob } ( \theta ^ { \prime } | \theta , \overline { D } _ { m } , a _ { n } )$"，其中"$\theta ^ { \prime } , \theta \in \Theta \text { and } \sum _ { \theta ^ { \prime } \in \Theta } \operatorname { Prob } ( \theta ^ { \prime } | \theta , \overline { D } _ { m } , a _ { n } ) = 1$"。
定义状态$\theta$中$\left(\bar{D}_{m}, a_{n}\right)$的代价映射："$f _ { \text {cost} } : \Theta \times \overline { D } \times A \rightarrow R$",防守方需要最小化代价，而攻击方则要最大化代价，因双方为0和博弈，因此我们有：

$$f_{\cos t}\left(\theta, \bar{D}_{m}, a_{n}\right)=f_{\cos t}^{a}\left(\theta, \bar{D}_{m}, a_{n}\right)=-f_{\cos t}^{d}\left(\theta, \bar{D}_{m}, a_{n}\right)$$
对于所有的网络状态$\Theta$则有：
$$\begin{aligned} \bar{f}(\theta) &=\left[f\left(\theta, \bar{D}_{1}\right), f\left(\theta, \bar{D}_{2}\right), \ldots, f\left(\theta, \bar{D}_{2^{N}}\right)\right]^{T} \\ \bar{g}(\theta) &=\left[g\left(\theta, a_{1}\right), g\left(\theta, a_{2}\right), \ldots, g\left(\theta, a_{M}\right)\right]^{T} \\ \mathcal{F}_{s} &=\left[\bar{f}\left(\theta_{1}\right), \bar{f}\left(\theta_{2}\right), \ldots, \bar{f}\left(\theta_{s}\right)\right]^{T} \in \mathcal{F} \\ \mathcal{G}_{s} &=\left[\bar{g}\left(\theta_{1}\right), \bar{g}\left(\theta_{2}\right), \ldots, \bar{g}\left(\theta_{s}\right)\right]^{T} \in \mathcal{G} \end{aligned}$$
定义代价折扣函数：$\vartheta_{\beta}: \Theta \times \mathcal{F} \times \mathcal{G} \rightarrow \mathbb{R}$，其中$\vartheta_{\beta}=\sum_{c=0}^{\infty} \beta^{c} \mathbb{E}_{\mathcal{F}_{s}, \mathcal{G}_{s}}\left\{f_{c o s t}\left(\theta, \bar{D}_{m}, a_{n}\right)\right\}$，定义："$\vartheta _ { \beta } = [ \vartheta _ { \beta } ( \theta _ { 1 } ) , \vartheta _ { \beta } ( \theta _ { 2 } ) , \ldots , \vartheta _ { \beta } ( \theta _ { s } ) ] ^ { T }$"
则通过定理：
$$\left. \begin{array}{l}{ \vartheta _ { \beta } ^ { N + 1 } ( \theta ) = \operatorname { val } ( R ( \theta ) ) }\\{ [ R ] _ { m n } = f _ { \cos t } ( \theta , \overline { D } _ { m } , a _ { n } ) + \beta \sum _ { \theta ^ { \prime } \in \Theta } \operatorname { Prob } ( \theta ^ { \prime } | \theta , \overline { D } _ { m } , a _ { n } ) }\\{ \times \vartheta _ { \beta } ^ { N } ( \theta ^ { \prime } ) }\end{array} \right.$$
则最优策略可通过下式获得： $$\left(\bar{f}^{*}(\theta), \bar{g}^{*}(\theta)\right) \in \arg \operatorname{val}(\mathcal{R}(\theta))$$
获得最优策略中的一个重要步骤就是计算博弈矩阵$\mathcal{R}(\theta)$.当给定矩阵$\mathcal{R}(\theta) \in \mathbb{R}^{N \times M}$,可通过下列线性过程获得平衡鞍点：
$$\begin{array}{ll}\max & y^{T} \mathbf{1}_{N} \quad \text { s.t. } \mathcal{R}^{T} y \leq \mathbf{1}_{M}, \quad y \geq 0 \\ \min z^{T} \mathbf{1}_{M} & \text { s.t. } \mathcal{R} z \geq 1_{N}, z \geq 0\end{array}$$

B. Defense Scheme-Based Estimator

估计器用于估计由于攻击而损失的信号，表达式如式（11）。
$\hat{x}(k+1)=\left\{\begin{array}{ll}A \hat{x}(k)+B u(k)-L_{0 \theta} C \hat{x}(k), & k \in \Gamma(0, k) \\ A \hat{x}(k)+B u(k)+L_{1 \theta} C e(k), & i=0 \\ k & \in \Psi(0, k) \\ i=1\end{array}\right. \tag{11}$
$L_{i \theta}$为收益，$e(k)$为估计误差。估计器其实取决于具体的防御机制，不同的策略会使网络状态$\theta$和子模型i不同。

C. Sliding Dynamic Analysis

设计带有攻击信息的滑模曲面函数如下：

$$s(k)=G_{i \theta} \hat{x}(k)-G_{i \theta}\left(A+B K_{i \theta}\right) \hat{x}(k-1)$$
这里"$i \in \{ 0,1 \} , \theta \in \Theta , G _ { i \theta }$"为预定义矩阵，$G_{i \theta}B$非单，$K_{i \theta}$为设计的矩阵。由此可得等价控制如式（12）。
$u_{e q}(k)=\left\{\begin{array}{ll}K_{0 \theta} \hat{x}(k)+\bar{g}_{0 \theta} L_{0 \theta} C \hat{x}(k), & i=0 \\ K_{1 \theta} \hat{x}(k)-\bar{g}_{1 \theta} L_{1 \theta} C e(k), & i=1\end{array}\right. \tag{12}$
这里"$\overline { g } _ { i \theta } = ( G _ { i \theta } B ) ^ { - 1 } G _ { i \theta }$"。将式（12）代入式（10）并将估计误差记为"$e ( k ) = x ( k ) - \hat { x } ( k )$"可得两个case
case1,攻击成功，则有式（13）
$\hat{x}(k+1)=\bar{A}_{0 \theta} \hat{x}(k)$
$e(k+1)=A e(k)+L_{0 \theta} C \hat{x}(k)+E \omega(k) \tag{13}$
这里"$\overline { A } _ { 0 \theta } = A + B K _ { 0 \theta } + B \overline { g } _ { 0 \theta } L _ { 0 \theta } C - L _ { 0 \theta } C$"
case2，无攻击则有式（14）
"$\left. \begin{array} { l } { \hat { x } ( k + 1 ) = \overline { A } _ { 1 \theta } \hat { x } ( k ) + \overline { L } _ { 1 \theta } e ( k ) } \\ { e ( k + 1 ) = ( A - L _ { \theta } ) e ( k ) + E \omega ( k ) } \end{array} \right. \tag{14}$"

这里"$\overline { A } _ { 1 \theta } = A + B K _ { 1 \theta } , \overline { L } _ { 1 \theta } = L _ { 1 \theta } C - B \overline { g } _ { 1 \theta } L _ { 0 \theta }$"
可见攻击无法一直持续，因为防御措施会使动态切换一直处于式(13)和式（14）之间，切换模型如式（15）。
$\xi(k+1)=F_{i} \xi(k)+\bar{E}_{i} \omega(k) \tag{15}$
其中参数具体如下: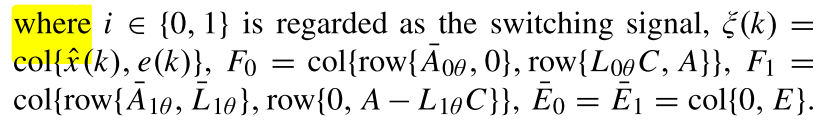
结论：式(15)中的系统一定可以指数平滑，且消退率为"$\tilde { l } = \lambda ^ { \frac { 2 \ln \mu } { - \tau } D \ln \lambda } + 1$"

D. Resilient Sliding Mode Control Design With Defense Strategy

恶意攻击者通过DoS攻击来破坏系统，让数据丢失从而使系统不稳定，设计好防御机制后应该测试其有效性。定义映射：$\Theta \times \mathcal{F} \times \mathcal{G} \rightarrow \mathbb{R}, S_{1}: \Theta \times \overline{\mathbb{D}} \times \mathcal{A} \rightarrow \mathbb{R}$来表示服务质量，则DoS攻击在状态$\theta$的攻击率可由如下映射一表示

$$r_{0 \theta}=S(\theta, \bar{f}(\theta), \bar{g}(\theta))=\bar{f}^{T}(\theta) \bar{S}_{1}(\theta) \bar{g}(\theta)$$
这里"$[ \overline { S } _ { 1 } ( \theta ) ] _ { m n } = S _ { 1 } ( \theta , \overline { D } _ { m } , a _ { n } )$"
因为性能取决于当前的action pair$(\bar{f}(\theta),\bar{g}(\theta))$，定义映射：$\Omega_{1}: \Theta \times \mathcal{F} \times \mathcal{G} \rightarrow \mathbb{R}$ and $\Omega_{2}: \Theta \times \mathbb{D} \times \mathcal{A} \rightarrow \mathbb{R}$,则性能$\hat{\gamma} _{\theta}$可被表示为如下映射二: $$\hat{\gamma}_{\theta}=\Omega_{1}(\theta, \bar{f}(\theta), \bar{g}(\theta))=\bar{f}^{T}(\theta) \Omega(\theta) \bar{g}(\theta)$$
这里有"$[ \Omega ( \theta ) ] _ { m n } = \Omega _ { 2 } ( \theta , D _ { m } , a _ { n } )$"
结合以两个映射便可获得最优收益"$L _ { i \theta } , K _ { i \theta }$"和最优策略"$F _ { s } ^ { * } \text { and } G _ { s } ^ { * }$"，如算法2：

Example2

对于系统（10）和给定参数，如下图：

系统响应如图7

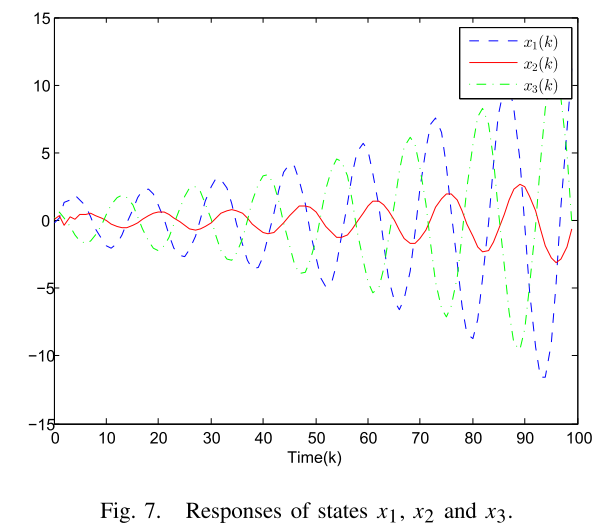
可知轨迹无法收敛。
当防御策略和攻击策略如表1，2，转换概率如表3时

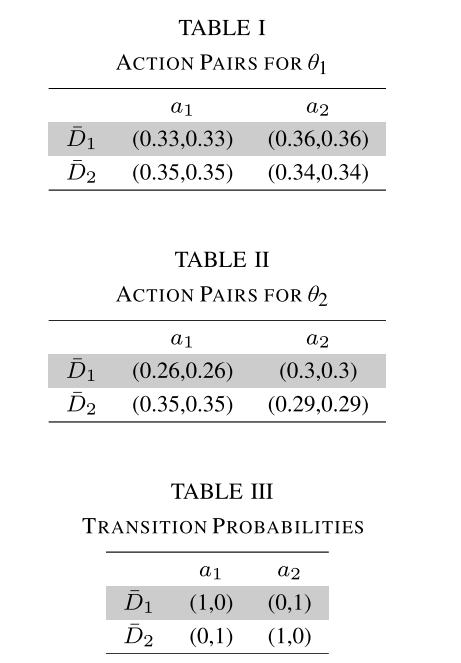
通过应用算法2，博弈值的迭代过程如图8所示

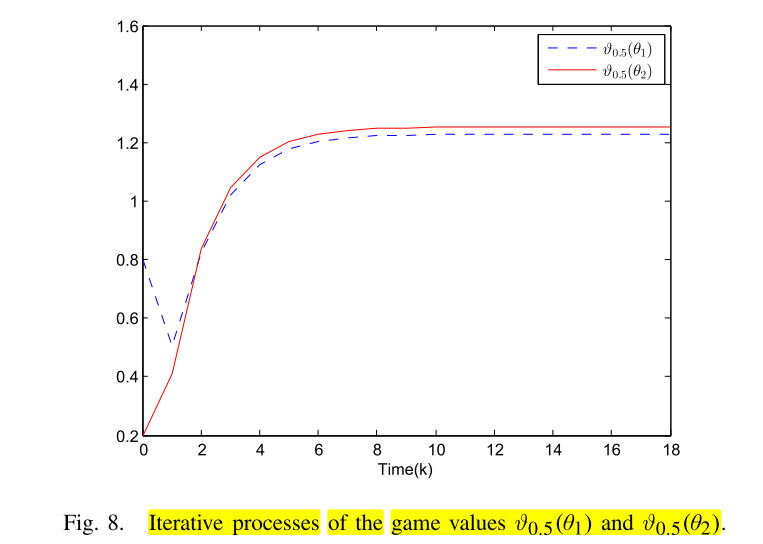
$f(\theta),g(\theta)$的进化过程如图9和图10

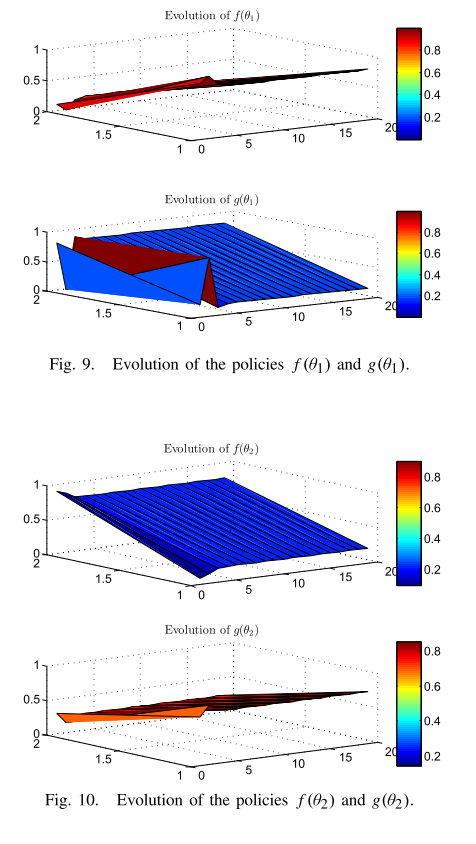
从这些图中可得知损失的数据可被有效地observed，且当DoS攻击发生时本文提出的弹性控制算法能有效地维护系统的稳定性。