@xiaoziyao
2020-06-30T14:40:00.000000Z
字数 2882
阅读 1882
P3651 展翅翱翔之时 (はばたきのとき)解题报告
解题报告
注意:“环套树”与“基环树”意思均为一棵树上增加一条边后形成的图,本文采取“基环树”的叙述方式。
题意
题意:给定个点,每个点都会依赖另一个点,可以用一定的代价改变一个点依赖的点,求让依赖关系变为环的最小代价。
数据范围:。
分析
首先,我们可以将点之间的依赖关系看为边(被依赖的点连向依赖别的点的点),这样依赖关系组成的图就会成为一个基环树森林。(简单证明一下:因为每个点只依赖一个点,所以只会有一条入边,即每一个大小为的森林至多有条边,即为一棵基环树)
为了将这张图最终变为一个环,我们可以把每一个基环树拆成若干个链(链的根节点可以连向其他的点),然后将链首尾相连就可以得到环了。这样我们就可以只考虑一棵基环树,最后将答案相加。
我们看一个例子吧:
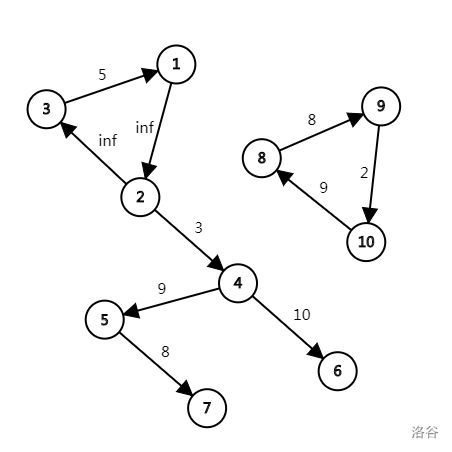
最优的做法是将断开,得到条链:
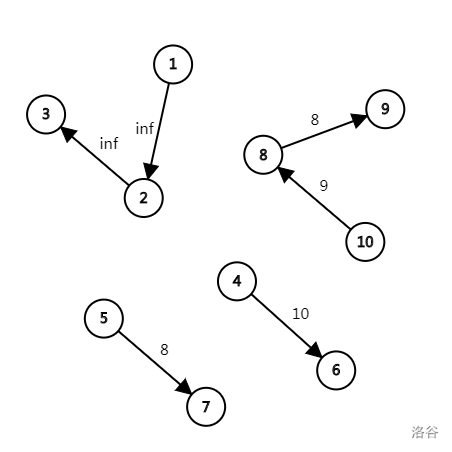
然后将条链首尾相连,得到答案:
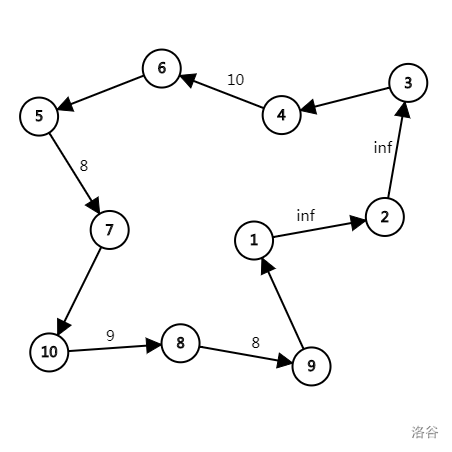
然后我们考虑每一棵基环树,因为每棵树只有一条入边,在环上的点都已经有了一条入边,只能向外连出边,因此这棵基环树显然是外向树。
对于每一棵根结点在环上的树,为了将其变为链,我们最多可以保留一个儿子,让它自己及其保留的儿子,保留的儿子保留的儿子……让这些点形成一条链。我们可以用贪心的思想,对于每个点我们保留它出边中费用最大的边,其他的边全部断掉,这样的话费一定是最小的。
(如在例子中断掉的)
这样就可以写出处理树部分的代码了:
void dfs(long long x,long long last){if(vis[x]==0)vis[x]=1;for(long long i=start[x];i;i=then[i]){long long y=to[i];if(y==last||vis[y]==2)continue;dfs(y,x);if(worth[out[x]]>worth[i])ans+=worth[i];else ans+=worth[out[x]],out[x]=i;}}
经过这样的处理,我们就只剩一个环及这个环上的点连出的一些链了。
我们先找一下当前基环树的环,这个部分代码是很容易写出来的(代表点访问过,代表点在环上):
void find(long long x){top=0;while(vis[x]==0)vis[x]=1,x=f[x];while(vis[x]==1)stk[++top]=x,vis[x]=2,x=f[x];}
此时,数组中存储的便是环上的点了。
考虑维护两个值:当前没有将整个环断成链的花费与当前已经将整个环断成链的花费。
我们思考一下,如何将当前剩下的点断成若干条链呢?发现环断开后只能带上一个点连出的链,而其他的链都必须断开。我们枚举每一个点,断开连入这个点的边,或者断开这个点带上的链,第一种操作会让之前的链保留下来(而上一个点带上的链可以与环上截下来的链成为新的链),第二种操作则可以维护现在链的形态。经过这样的操作,剩下的所有点都被分割为若干条链了。
我们注意一下:第一种操作会让一个没有断成链的环断成链(当然也可以让一个断成链的环断成更多的链),第二个操作则不会改变环的形态。因此可以从两种操作转移(第一种操作可以从与转移来,而第二种操作只能从转移来),而只能从第二种操作转移(且由转移过来)。
还是举个例子吧:
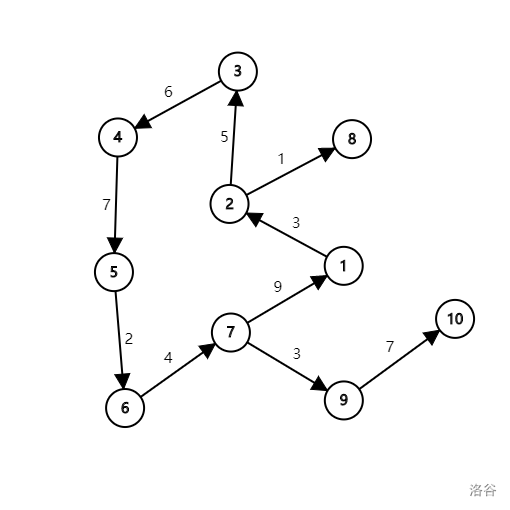
这个例子的答案应该是割掉和,为,至于为什么,读者自证不难。
最后把答案累加就可以了。
这一部分的代码:
long long cut0=0,cut1=inf;for(j=1;j<=top;j++)dfs(stk[j],0);for(j=1;j<=top;j++){cut1=min(min(cut0,cut1)+worth[in[stk[j]]],cut1+worth[out[f[stk[j]]]]);cut0+=worth[out[f[stk[j]]]];}ans+=cut1;
由于在函数与函数中每个点都只会遍历一遍,循环也只会将每个环及里面的点遍历一遍,因此复杂度是的。
代码
注:与分别指连向的边编号与连出的边的编号。
#include<stdio.h>#define inf 1000000000000000000const int maxn=100005,maxm=200005;long long i,j,k,m,n,e,ans,top;long long start[maxn],to[maxm],then[maxm],worth[maxm],f[maxn],in[maxn],out[maxn],vis[maxn],stk[maxn];inline long long min(long long a,long long b){return a<b? a:b;}inline void add(long long x,long long y,long long z){then[++e]=start[x],start[x]=e,to[e]=y,worth[e]=z;}void find(long long x){top=0;while(vis[x]==0)vis[x]=1,x=f[x];while(vis[x]==1)stk[++top]=x,vis[x]=2,x=f[x];}void dfs(long long x,long long last){if(vis[x]==0)vis[x]=1;for(long long i=start[x];i;i=then[i]){long long y=to[i];if(y==last||vis[y]==2)continue;dfs(y,x);if(worth[out[x]]>worth[i])ans+=worth[i];else ans+=worth[out[x]],out[x]=i;}}int main(){scanf("%lld",&n);for(i=1;i<=n;i++){long long x;scanf("%lld%lld",&f[i],&x);in[i]=i,add(f[i],i,x);}for(i=1;i<=n;i++){if(vis[i])continue;find(i);if(top==n){puts("0");return 0;}long long cut0=0,cut1=inf;for(j=1;j<=top;j++)dfs(stk[j],0);for(j=1;j<=top;j++){cut1=min(min(cut0,cut1)+worth[in[stk[j]]],cut1+worth[out[f[stk[j]]]]);cut0+=worth[out[f[stk[j]]]];}ans+=cut1;}printf("%lld\n",ans);return 0;}
