@wxf
2018-09-12T00:10:13.000000Z
字数 6712
阅读 6574
4.整数的二进制表示与位运算
老马说编程
上节我们提到正整数相乘的结果居然出现了负数,要理解这个行为,我们需要看一下整数在计算机内部的二进制表示。
十进制
要理解二进制,我们首先看一下熟悉的十进制。下面以123为例,我们看一看它的含义是什么。
其实123表示的含义是。;也就是:之和
系数:每个位置上的数值
基数:X进制,那么基数就是X
权:对该数据系数由右到左进行编号,且从0开始,每个编号就是该系数对应的权
二进制
计算机中电子元器件的特性,决定了计算机的信息数据只能用二进制数来处理。在程序中,即使是用十进制数和文字等记述的信息,在编译后也会转为二进制的值,所以,程序运行时计算机内部处理的也是用二进制数表示的信息。
对于用二进制数表示的信息,计算机不会区分它是数值、文字或某种图片的模式等,而是根据我们对计算机发出的指示来进行信息的处理(运算)。例如00100111这样的二进制数,既可以视为纯粹的数值作加法运算,也可以视为“‘”(单引号)文字而显示在显示器上,或者视为■■□■■□□□这一图形模式印刷出来。具体进行何种处理,取决于程序的编写方式。
在对二进制有了初步了解以后,我们接下来说说整数在计算机中的二进制表示。
正整数的二进制表示
正整数的二进制表示非常简单。我们来看一些例子,如下:
| 二进制 | 位权运算 | 十进制 |
|---|---|---|
| 10 | 2 | |
| 11 | 3 | |
| 111 | 7 | |
| 1010 | 10 |
负整数的二进制表示
我们都知道十进制的负数就是在数值前面加一个负数符号(-),如:-123。但是二进制如何表示负数呢?其实概念是类似的,二进制使用最高位表示符号位,1表示负数,0表示正数。但是,在计算机中负数的表示不是简单的将最高位变为1,比如说:
(为方便举例,下面假定类型是byte,即从右到左的第8位表示符号位)
;
- byte a = -1,如果只是将最高位变为1,二进制应该是10000001,但实际上,它却是11111111。
- byte a = -127,如果只是将最高位变为1,二进制应该是11111111,但实际上,它却是10000001。
这是什么表示法呢?这是补码表示法。计算机在做减法运算时,实际上内部是在做加法运算。比如说,当计算7-3时,可以变成7+(3的补数)。所以补数就是用正数来表示负数。另外,希望大家牢记“在计算机系统中,数值一律采用补码来表示(存储)的。”
为了获得补数,我们需要将二进制数的各数位的数值全部取反[1],然后再将结果加1。例如:
- 1的补数:1的原码是00000001,反码是11111110,然后加1,结果就是11111111。
- 2的补数:2的原码是00000010,反码是11111101,然后加1,结果就是11111110。
- 127的补数:127的原码是01111111,反码是10000000,然后加1,结果就是10000001。
其实,补数求解的变换方法就是数学中的求相反数[2]。后面会讲到。所以,希望大家能够牢记“将二进制数的值取反后加1的结果,和原来的值相加,结果为0”这一法则。
若给定一个负数的二进制表示,如何计算它的十进制值呢?毫无疑问,我们可以采用补数求解的变换方法。比如:10010010,首先取反得到01101101,然后加1得到01101110,转换成十进制后为110,所以其原值为-110。
十进制与二进制对照表:
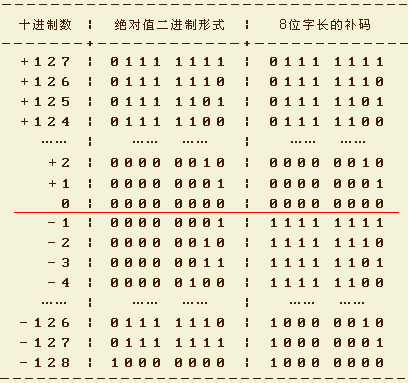
为什么要采用补码
补码表示形式,虽然直观上不易理解,但是逻辑上去非常严谨。例如,计算1-1(其实是 1+(-1))用原码表示,其计算结果如下:
1 -> 00000001
-1 -> 10000001
+ ——————
-2 -> 10000010
用符合直觉的原码表示,1-1的结果是-2。
如果使用补码表示,其计算结果如下:
1 -> 00000001
-1 -> 11111111
+ ——————
0 ->1 00000000
1+(-1)的运算结果为0,是正确的。最高位溢出会被忽略。
再比如,5-3:
5 -> 00000101
-3 -> 11111101
+ ——————
2 -> 00000010
理解了二进制加减法,我们就能理解为什么正数的运算结果可能出现负数了。当计算结果超出表示范围的时候,最高位往往是1,然后就会被看做负数。比如说:127+1:
127 -> 01111111
1 -> 00000001
+ ———————
-128 -> 10000000
深入理解补码
通过上面的描述我们知道了负数在计算机中是通过补码的方式表示的,下面让我们对原码、反码和补码做个详细了解。
原码
对于正数,原码表示与真值[3]相同;对于负数,符号位1加上整数部分的绝对值。比如:
- +1的8位二进制原码表示为:0 0000001;
- -1的8位二进制原码表示为:1 0000001;
反码
正数的反码是其本身;负数的反码是在原码基础上,符号位不变,其余各位取反。比如:
- [+1]==
- [-1]==
补码
正数的补码是其本身;负数的补码就是反码基础上加1。比如:
- [+1]===
- [-1]===
综上所述:
· 正数的原码,反码,补码都相同。
· 负数的原码就是符号位1加上整数部分的绝对值;
反码在原码的基础上,符号位不变,其余各位取反;
补码是反码基础上加1。
十六进制
二进制写起来太长,为了简化书写,将4个二进制简化为一个0到15的数,10-15用字符A-F表示,称这种表示方式为16进制,如:
| 2进制 | 10进制 | 16进制 |
|---|---|---|
| 1010 | 10 | A |
| 1011 | 11 | B |
| 1100 | 12 | C |
| 1101 | 13 | D |
| 1110 | 14 | E |
| 1111 | 15 | F |
在Java中可以用16进制直接写常量数字,在数字前面加0x即可。比如10进制123,用16进制表示就是0x7B,即123 = 。给整数赋值或进行运算时,都可以直接使用16进制,如:
int a = 0x7B;
注意:Java中不支持直接写二进制常量,比如,想表示二进制形式的11001,Java中不能直接写11001。需要将其补足8位,即00011001。然后用16进制表示,即0x19;
查看整数的二进制和十六进制表示
在Java中,可以方便的是用Integer和Long的方法查看整数的二进制和十六进制表示,例如:
int a = 25;System.out.print(Integer.toBinaryString(a)); //二进制System.out.print(Integer.toHexString(a)); //十六进制System.out.print(Long.toBinaryString(a)); //二进制System.out.print(Long.toHexString(a)); //十六进制
进制换算
十进制换算成其他进制
1.十进制转换为二进制
十进制转换为二进制,分为整数部分和小数部分
整数部分
方法:除以基数反取余,即除以2反取余。
示例:将十进制的21转换为二进制数。
21 / 2 = 10 -- 1
10 / 2 = 5 -- 0
5 / 2 = 2 -- 1
2 / 2 = 1 -- 0
1 / 2 = 0 -- 1
二进制(反取余数):00010101小数部分
方法:乘以基数取整,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,直到小数部分为0为止。若永远不能为0,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍。如果是零,舍掉;如果是1,则近1。读数要从前面的整数读到后面的整数。
示例:
例1:将0.125换算为二进制数。
0.125 * 2 = 0.25 -- 0
0.25 * 2 = 0.5 -- 0
0.5 * 2 = 1.0 -- 1
二进制:0.001例2:将0.45转算为二进制数(保存到小数点第四位)。
0.45 * 2 = 0.9 -- 0
0.9 * 2 = 1.8 -- 1
0.8 * 2 = 1.6 -- 1
0.6 * 2 = 1.2 -- 1
二进制:0.0111
2.十进制转换为八进制
十进制转八进制有两种方法:
- 间接法:先将十进制转换成二进制,然后将二进制在转换为八进制
直接法:因为八进制是由二进制衍生而来的,因此我们可以采用与十进制转二进制相类似的方法。下面一起对整数部分和小数部分的转换进行具体介绍:
- 整数部分
方法:除以基数反取余,即除以8反取余。 - 小数部分
方法:乘以基数取整,即乘8取整。
示例:将十进制数796.703125转换为八进制数, 首先将这个数字分为整数部分796和小数部分0.703125。
整数部分 小数部分 796/8 = 99 -- 4
99/8 = 12 -- 3
12/8 = 1 -- 4
1/8 = 0 -- 1
0.703125 x 8= 5.625 -- 5
0.625 x 8 = 5.0 -- 5八进制数:1434.55 - 整数部分
3.十进制转换为十六进制
十六进制和八进制有很多相似之处,大家可以参照上面十进制转八进制,自己尝试这两个进制之间的转换。
十进制和十六进制对照表:
| 十进制 | 十六进制 | 十进制 | 十六进制 | 十进制 | 十六进制 |
|---|---|---|---|---|---|
| 0 | 00 | 10 | 0A | 20 | 14 |
| 1 | 01 | 11 | 0B | 30 | 1E |
| 2 | 02 | 12 | 0C | 40 | 28 |
| 3 | 03 | 13 | 0D | 50 | 32 |
| 4 | 04 | 14 | 0E | 60 | 3C |
| 5 | 05 | 15 | 0F | 70 | 46 |
| 6 | 06 | 16 | 10 | 80 | 50 |
| 7 | 07 | 17 | 11 | 90 | 5A |
| 8 | 08 | 18 | 12 | 100 | 64 |
| 9 | 09 | 19 | 13 | …… | …… |
其他进制换算成十进制
1.二进制转换为十进制
方法:按权相加法,即将二进制每位上的数乘以权,然后相加之和即是十进制数。(不分整数和小数部分)
示例:将二进制数101.101转换为十进制数。
| 整数部分 | 小数部分 |
|---|---|
| 十进制: | |
2.八进制转换为十进制
方法:按权相加法,即将八进制每位上的数乘以位权,然后相加之和即是十进制数。
示例:将八进制数67.35转换为十进制数。
| 整数部分 | 小数部分 |
|---|---|
| 十进制: | |
3.十六进制转换为十进制
方法:按权相加法,即将十六进制每位上的数乘以位权,然后相加之和即是十进制数。
示例:将十六进制数61.45转换为十进制数。
| 整数部分 | 小数部分 |
|---|---|
| 十进制: | |
二进制、八进制、十六进制之间的转换
1.二进制与八进制之间的转换
- 二进制转换为八进制
方法:取三合一法,即从二进制的小数点为分界点,向左(向右)每三位取成一位,如果不够位数,整数补高位,小数补低位。接着将这三位二进制按权相加,得到的数就是一位八位二进制数,然后,按顺序进行排列,小数点的位置不变,得到的数字就是我们所求的八进制数。
示例 :将二进制数1101.1转换为八进制数。
001 101.100
1 5. 4
得到八进制数:15.4 - 八进制转换为二进制
方法:取一分三法,即将一位八进制数分解成三位二进制数,用三位二进制按权相加去凑这位八进制数,小数点位置照旧。
示例 :将八进制数15.4转换为二进制数。
1 5. 4
001 101.100
得到二进制数:00001101.100
2.二进制与十六进制之间的转换
- 二进制转换为十六进制
方法:与二进制与八进制转换相似,只不过是一位(十六)与四位(二进制)的转换,下面具体讲解。
示例:将二进制数11101001.1011转换为十六进制数。
1110 1001.1011
E 9. B
得到十六进制:E9.B - 十六进制转换为二进制
方法:取一分四法,即将一位十六进制数分解成四位二进制数,用四位二进制按权相加去凑这位十六进制数,小数点位置照旧。
示例:将十六进制6E.2转换为二进制数
6 E. 2
0110 1110.0010
得到二进制:1101110.001
3.八进制与十六进制的转换
方法:一般是将八进制(或十六进制)转换为二进制,然后再将二进制转换为十六进制(或八进制),小数点位置不变。那么相应的转换请参照上面二进制与八进制的转换和二进制与十六进制的转
位运算
位运算是将数据看做二进制,进行位级别的操作。位运算有移位运算和逻辑运算。位运算只适用于整型数据,对float和double类型进行位运算操作会报错。
移位运算
- 左移
<<:向左移动,右边的低位补0,高位溢出就舍掉。左移1位就相当于乘以2。 - 有符号右移
>>:向右移动,右边的舍掉,左边补符号位,即原来最高位是1就补1,原来最高位是0就补0。右移1位相当于除以2。(算术右移) - 无符号右移
>>>:向右移动,右边的舍掉,左边补0。(逻辑右移)
逻辑运算
按位与
&:两位都为1才为1
应用场景:判断奇偶。
依据:根据最末位是0还是1来决定,若为0就是偶数,为1就是奇数。
比较:可以使用if((a&1) == 0)代替if(a % 2 == 0)来判断变量a是否为偶数。
代码:输出0至100之间的所有奇数for(int i = 0; i < 100; i++){if((i&1) == 1){System.out.println(i);}}
按位或
|:只要有一位为1,就为1按位取反
~:1变为0,0变为1
应用场景:变换符号(正数变成负数,负数变成正数)
代码:求相反数public int signReversal(int a){return ~a + 1; //取反后加1}
求绝对值(取反加1)
代码:求绝对值public int myAbs(int a){int i = a >> 31; //利用位移运算取符号位,若a为正数,i等于0;若a为负数,i等于-1。return i == 0 ? a : (~a + 1);}
或
//对于任何数,与0异或都会保持不变,与-1即0xFFFFFFFF异或就相当于取反。//因此,a与i异或后再减i(因为i为0或-1,所以减i即是要么加0要么加1)也可以得到绝对值。public int myAbs(int a){int i = a >> 31;return ((a^i) - i);}
按位异或
^:相异为真,相同为假
规律:
1.一个数与自身异或其结果为0;任何数与0异或都不会变;与-1异或就相当于取反。
2. 多个整数相^的结果跟顺序无关。应用场景:
交换两个数的值
代码:不使用第三方变量实现交换两个数public void swap(int a, int b){if(a != b){a = a^b;b = b^a;a = a^b;}}
或者使用符合操作符,如下
public void swap(int a, int b){if(a != b){a ^= b;b ^= a;a ^= b;}}
分析: 1.a ^= b 即 a = a^b; 2.b ^= a 即 b = a^b = (a^b)^b;根据异或的两个规律可以得出b = a^b^b = a,所以此时b被附上了a的值。 3.a ^= b 即 a = a^b;由第一步可知a = (a^b),由第二步可知b = a。所以a = a^b = (a^b)^a。故a会被附上b的值。
其他位运算使用场景
本节讨论的内容包括整数的二进制表示、进制换算、整数的位运算。在下一节的内容中我们讨论一下小数的二进制。
参考资料:
- 老马说编程(微信号:laoma_shuo)——整数的二进制表示与位运算
- 位操作基础篇之位操作全面总结
- 二进制、八进制、十进制、十六进制之间转换
- 《程序是怎样跑起来的》
[1] 这里所说的取反是指,把二进制数各数位的0变成1,1变成0,即位运算中的按位取反(~)操作。例如00000001这个8位二进制数取反后就变成了11111110。 ↩
[2] 相反数定义:只有符号不同的两个数互为相反数。相反数的绝对值相同。例如:-2与+2互为相反数。 ↩
[3] 我们需要知道两个概念,(1)机器数;(2)真值。
机器数:一个数在计算机中的二进制表示形式。比如:十进制中的+3,其换算成二进制就是00000011;-3换算成二进制就是10000011。那么这里的00000011和10000011就是机器数。
真值:因为计算机中第一位是符号位,所以机器数的形式值就不一定等于真正的数值。比如:上面的有符号数10000011,其最高位1代表负,起真正数值是-3,而不是形式上的131(10000011换算成十进制是131)。所以为区别起见,将带符号位的机器数对应的真正数值称为真值。 ↩
