[关闭]
@sensitive-cs 2017-06-16T03:57:44.000000Z 字数 10787 阅读 2471

　　　最小生成树的几个算法编程及实现

　　　　　　　　　　——Prim算法、Kruskal算法和破圈法

　　　　　　　　　　　　　　　　　　摘要

　　连通图广泛应用于交通建设，求连通图的最小生成树是最主要的应用。比如要在n个城市间建立通信联络网，要考虑的是如何保证n点连通的前提下最节省经费，就应用到了最小生成树。而要求解最小生成树先要了解其概念即是对于一个无向连通图g=(v,e)，给它的每条边(u,v)一个权值w(u,v)。若图g的生成树不止一个，那么其中包含的n-1条边的权值之和最小的生成树就是图g的最小生成树。
　　求图的最小生成树最常见有三种算法，一种是Prim（普里姆）算法【1】，另一种是Kruskal（克鲁斯卡尔）【2】算法，还有一种是破圈法【3】。本文从分析Prim、Kruskal和破圈法三种算法编程实现出发，通过对实际问题的求解、测试来详细介绍最小生成树的这三个算法编程及实现，并对Prim算法进行优化，最后进行总结。

关键词： Prim算法、Kruskal算法、破圈法、最小生成树、优先队列优化、图论

一、实验目的

1、了解最小生成树的几个算法
2、掌握图的存储表示
3、实现Kruskal算法、Prim算法和破圈法编程的实现
4、掌握用Kruskal算法、Prim算法和破圈法解决实际问题的方法

二、实验设计

　　本次课程设计，我们要解决如何用Prim算法、Kruskal算法以及破圈法解决最小生成树的问题，并最终编程实现这个算法。Prim算法、Kruskal算法以及破圈法是解决最小生成树的常见的有效地方法。我们决定通过对实际问题的求解和编程实现来进一步体现和实现这三种算法。在对问题求解的过程中，我们会详细介绍这两种算法，并对Prim算法做出优化【4】。

三、实验过程

1、相关概念介绍
1.1 树
一个连通且无圈（回路）的无向图称为一棵树
1.2 生成树
给定图g=< v,e >,若g的生成子图t是树，则称t是g的生成树
1.3 最小生成树
在一个带权图g的所有生成树中，树权最小的那棵生成树称为g的最小生成树
1.4 邻接矩阵表示无向带权图
给定图g=< v,e >，作一个v*v的矩阵，avi，vj=vi与vj的权值。
1.5 利用Kruskal算法求最小生成树
　　先构造一个只含n个顶点、而边集为空的子图，把子图中各个顶点看成各棵树上的根结点，之后，从网的边集E中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，即把两棵树合成一棵树，反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直到森林中只有一棵树，也即子图中含有 n-1 条边为止。
　　时间复杂度为为O(e^2), 使用并查集优化后复杂度为 O（eloge），与网中的边数有关，适用于求边稀疏的网的最小生成树。
1.6 利用Prim算法求最小生成树
1).输入：一个加权连通图，其中顶点集合为V，边集合为E；
2).初始化：Vnew = {x}，其中x为集合V中的任一节点（起始点），Enew = {},为空；
3).重复下列操作，直到Vnew = V：
a.在集合E中选取权值最小的边< u, v >，其中u为集合Vnew中的元素，而v不在Vnew集合当中，并且v∈V（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；
b.将v加入集合Vnew中，将< u, v >边加入集合Enew中；
4).输出：使用集合Vnew和Enew来描述所得到的最小生成树。
1.7 利用破圈法求最小生成树
1.7.1先将所有的边按权值进行降序排列
1.7.2之后对于取出的每一个边来说,判断其连接的两个结点是否具有圈.(即先删除次边,然后判断这两个结点是否连接,之后对删除的边进行恢复)
1.7.3对于有圈的,将这条边删除,否则,往下查找.
1.7.4算法结束:当剩下的边=结点数-1的时候.

2、算法具体介绍
2.1 克鲁斯卡尔具体介绍
2.1.1 详细流程
（1）选择未选择过的边中权重最小的一条边
（2）将所选边加入树中
（3）如果所选边和已选边构成回路，则舍弃
（4）重复上述1，2，3步骤直至检验所有边
2.1.2 流程图

Created with Raphaël 2.1.2开始选择未选边中最小边是否构成回路添加该条边是否已经遍历所有边Endyesnoyesno

（5）复杂度分析
　　首先用C++ STL中的sort函数对各边进行排序，复杂度为O(logn),之后遍历每条边的过程的复杂度是O(n),所以最终的复杂度是O(nlogn)。

2.2 破圈法具体介绍
2.2.1详细流程
（1）选择未选择的边中权值最大的一条边，并将这条边标记为不连通
（2）判断此时的图是否连通
（3）若连通，则从边的总权值中减去这条边的权值；若不连通，则将这条边重新标记为连通。
（4）重复上述1,2,3步骤，直到检验完所有的边
2.2.2 流程图

Created with Raphaël 2.1.2开始选择未选边中权值最大的边标记为不连通从总权值中减去此条边的权值判断图是否连通重新标记此条边连通加上这条边的权值是否已经遍历所有边Endyesnoyesno

（5）复杂度分析
　遍历所有的边，此时的时间复杂度为O(n),在每次去掉边，用深度优先搜索法判断每条边是否连通时，时间复杂度为O(n*n)，所以最后的时间复杂度为O(n*n*n)。

2.3 Prim算法具体介绍
2.3.1 详细流程
（1）将v中所有点标记为0，在v中任选一个点v1，并将其标记为1
（2）找出所有与v1邻接的边中权重最小的边，并判断另一个点是否标记为1
（3）若另一点标记为0，则联通这条边，并将该点标记为1；若另一点标记为1，则舍弃这条边
（4）重复2，3步骤，直到找到n-1条边
2.3.2 流程图

Created with Raphaël 2.1.2开始将v中所有点标记为0在未被选中的点中任选一个点v1标记为1选取与v1邻接边中权重最小的边该边另一点是否标记为1连通这条边,将该点标记为1是否遍历所有边endyesnoyesno

（5）时间复杂度分析
外循环循环n-1次用于加入n-1条边，内循环循环n次,用于更新各点到V中的点的最小距离，所以最后的时间复杂度是O(n*n)。

3、例题及介绍
（https://vjudge.net/problem/POJ-1251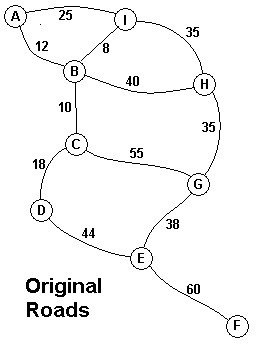）e7d66346fc0b337fad5f85d5fa5ce673.jpg-43.2kB
　　热带岛屿Lagrishan的长老们有一个麻烦。几年前，外国援助资金被用于村庄之间的额外公路上。但是丛林无情地侵蚀着道路，维护如此大的道路网络花费太过昂贵。长老会必须选择停止维持某些道路。上图显示所有使用中的道路以及现在每月的维护费用。当然，需要有道路保证所有村长之间的连通，即使路线没有以前那么短。行政长官想告诉老人如何在保证村庄都连通的情况下，每个月用最少的钱来维护道路。这些村庄在上面的地图上贴上了从A到I的标签。你的任务是编写一个程序来解决这样的问题。

3.1 利用Kruskal算法求解
（1）
定义一个结构体数组

  1. struct road
  2. {
  3.     int from,to;
  4.     int len;
  5. }e[80];

定义二维数组

  1.  int mp[30][2];

（2）
向二维数组输入权重数据， 并根据权重数据输入结构体数组
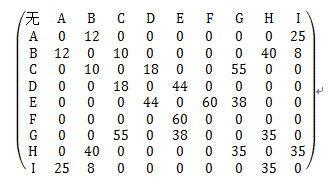
124.gif-6kB

（3）
利用并查法检验所有边得出最终结果对每一个点初始化，将每个点的根节点初始化为自己。

  1. void init(void)
  2. {
  3.     for (int i = 0;i < 30;i++)
  4.         par[i] = i;
  5. }

查询每一个点的根节点,用到了路径压缩的思想。

  1. int find(int x)
  2. {
  3.     if (x == par[x]) return x;
  4.     else return par[x] = find(par[x]);
  5. }

将一条边加入生成树中并判断是否成功。

  1. bool merge(int x,int y)
  2. {
  3.     x = find(x);
  4.     y = find(y);
  6.     if (x == y) return false;
  8.     par[x] = y;
  10.     return true;
  11. }

(4)
根据边权重对结构体数组进行排序

  1. bool cmp(struct road a,struct road b)
  2. {
  3.     return a.len < b.len;
  4. }

(5)
对排序后的数组进行一一检验

先选取权重为8的IB边并将I的根节点设为B的根节点
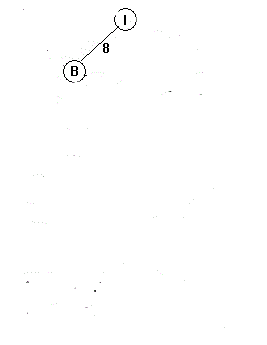
e7d66346fc0b337fad5f85d5fa5ce673 - 副本.gif-1.8kB
再选取权重为10的BC边连接并将C的根节点设为B的根节点
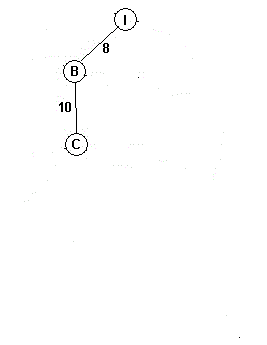
2.gif-1.9kB
再选取AB边连接并将B的根节点设为A的根节点
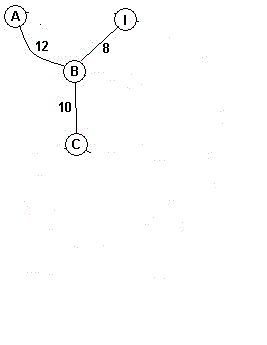
3.gif-2.2kB
再选取DC边链接并将D的根节点设为C的根节点
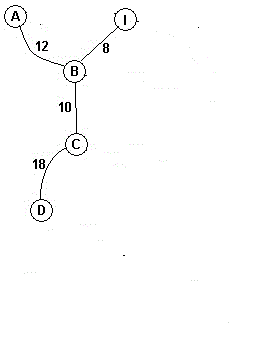
5.gif-2.4kB
再选取AI边，因为A的根节点和I的根节点相同，舍去
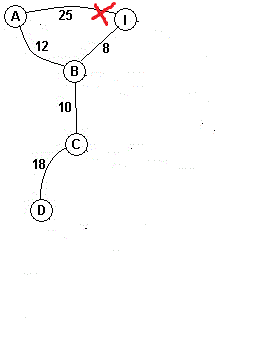
6.gif-2.7kB
再选取IH边，将H的根节点设为I的根节点
6.gif-2.5kB
再选取HG边，将G的根节点设为H的根节点
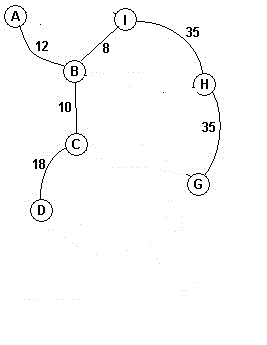
7.gif-2.8kB
再选取GE边，将E的根节点设为G的根节点
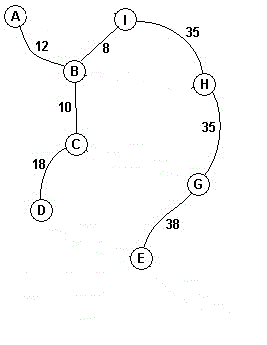
8.gif-3.1kB
选取BH边，B和H的根节点相同，舍去
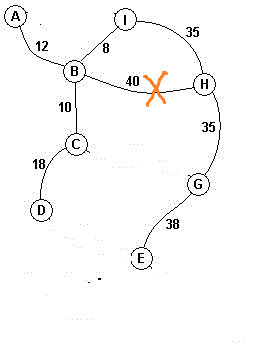
9.gif-3.5kB
选取DE边，D和E的根节点相同，舍去
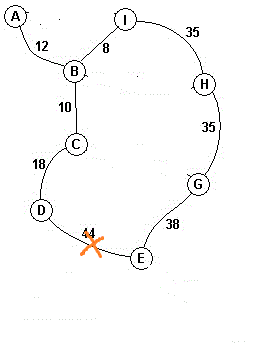
e7d66346fc0b337fad5f85d5fa5ce673 - 副本.gif-3.4kB
选取CG边，C和G的根节点相同，舍去

选取EF边
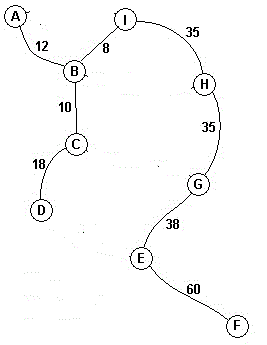
9.gif-3.3kB

提交结果：克鲁斯卡尔

*具体代码见附录

3.2 利用破圈法求解
（1）定义一个结构体数组用于保存边

  1. struct road
  2. {
  3.     int from,to;
  4.     int len;
  5. }e[80];

（2）定义一个0,1矩阵用于表示两点之间的连通情况

  1. mp[105][105];

(3) 用深度优先搜索dfs()函数检验每次去边后整个图是否连通

  1. void dfs(int x)
  2. {
  3.     v[x] = 1;
  5.     num++;
  7.     for (int i = 1;i <= n;i++)
  8.     {
  9.         if (!v[i] && mp[x][i])
  10.         {
  11.             dfs(i);
  12.         }
  13.     }
  14. }
  15. //if (num == n) connected

(4)具体步骤
完整图片
1.选取权重最大的边60，并且去掉这条边
第一步
发现图不连通所以将这条边恢复
恢复
2.选取权重第二大的边55并去掉
第二步
图是连通的，继续执行
3.选取权重为44的边并去掉
第三步
图是连通的，继续执行
4.选取权重为40的边并去掉
第四步
图是连通的，继续执行
5.选取权重为38的边并去掉
第五步
不连通，把边恢复
恢复
6.选取权重为35的边并去掉
第六步
图不连通，恢复边
恢复
7.选取权重为25的边并去掉
第七步
图是连通的，并且只有n-1条边，算法结束

提交结果：破圈法

*具体代码见附录

3.3 利用Prim算法求解
（1）输入各个点和两点之间边的距离

  1.   for (int i = 0;i < n - 1;i++)
  2.     {
  3.       char a[5];
  4.       int num;
  6.       scanf("%s",a);
  8.       scanf(" %d",&num);
  10.       for (int j = 0;j < num;j++)
  11.       {
  12.         char b[5];
  13.         int d;
  15.         scanf("%s",b);
  16.         scanf(" %d",&d);
  18.         int st = a[0] - 'A',en = b[0] - 'A';
  20.         mp[st][en] = mp[en][st] = d;
  21.       }
  22.     }

得到以下矩阵
12.gif-5.8kB
（2）初始化各点间对应的边为最小距离

  1.  for (int i = 0;i < n;i++)
  2.   {
  3.     lowcost[i] = mp[v][i];
  4.   }

(3)选取A点作为最初点，在未找取的点中找离A点最近的点B加入树中
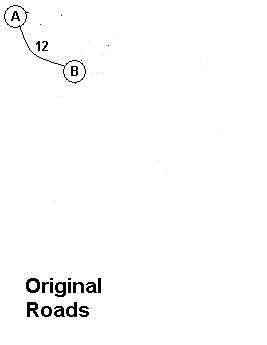
1.gif-2.1kB
(4)将B点加入树中并找取剩下点中离树中点最近的点I加入树中
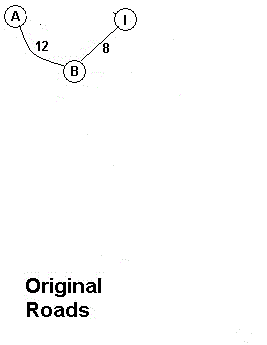
2.gif-2.3kB
(5)将I点加入树中并取去剩下点中离树中点最近的点C加入树中
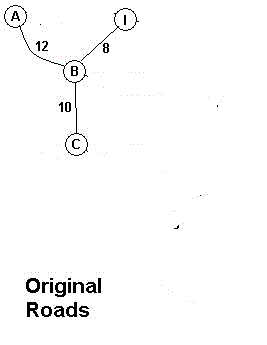
3.gif-2.5kB
(6)将C点加入树中并取去剩下点中离树中点最近的点D加入树中
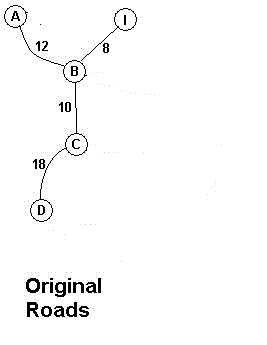
4.gif-2.7kB
(7)将D点加入树中并取去剩下点中离树中点最近的点H加入树中
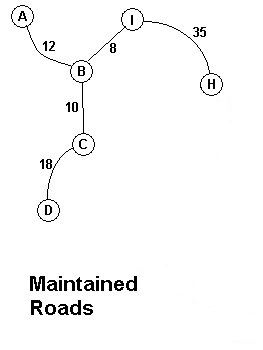
e7d66346fc0b337fad5f85d5fa5ce6.jpg-32.1kB
(8)将H点加入树中并取去剩下点中离树中点最近的点G加入树中
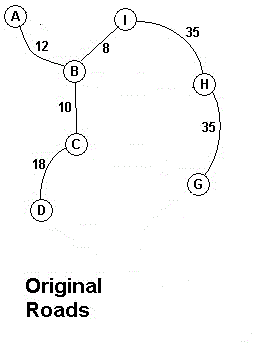
6.gif-3.2kB
(9)将G点加入树中并取去剩下点中离树中点最近的点E加入树中
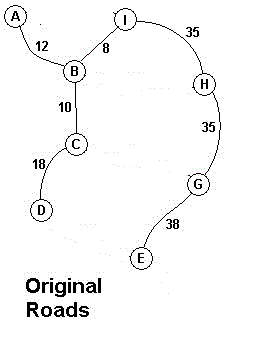
7.gif-3.4kB
(10)将E点加入树中并取去剩下点中离树中点最近的点F加入树中
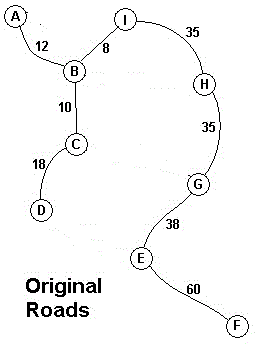
8.gif-3.6kB
没有更大的边，算法结束
提交结果：prim

3.3 Prim算法优化
　　我们分析了朴素的prim算法的复杂度为O(n*n)，在n的规模较小的情况下，程序的运行时间比较短，在可接受范围内。但是当n的规模比较大时，比如当n的规模达到10^6时，程序的运行时间将会超出1000ms。经查证可知，1000ms的程序的运行时间所允许的计算次数最多为10^8。所以，当n的规模比较大时，我们就需要对算法进行改进优化。
　　经查资料可知，C++ STL 中封装了一个名为优先队列的数据结构，基于堆实现。此数据结构的优点就是插入和读取元素的时间复杂度均为O(logn)，并且可以自定义优先级来读取元素，优先级高的元素先出队。
　　接下来以poj上的一道题为例，进行prim算法的优化。
题目链接：https://vjudge.net/problem/POJ-1258
题意：
Farmer John has been elected mayor of his town! One of his campaign promises was to bring internet connectivity to all farms in the area. He needs your help, of course.
Farmer John ordered a high speed connection for his farm and is going to share his connectivity with the other farmers. To minimize cost, he wants to lay the minimum amount of optical fiber to connect his farm to all the other farms.
Given a list of how much fiber it takes to connect each pair of farms, you must find the minimum amount of fiber needed to connect them all together. Each farm must connect to some other farm such that a packet can flow from any one farm to any other farm. The distance between any two farms will not exceed 100,000.

Input:
The input includes several cases. For each case, the first line contains the number of farms, N (3 <= N <= 100). The following lines contain the N x N conectivity matrix, where each element shows the distance from on farm to another. Logically, they are N lines of N space-separated integers. Physically, they are limited in length to 80 characters, so some lines continue onto others. Of course, the diagonal will be 0, since the distance from farm i to itself is not interesting for this problem.

Output:
For each case, output a single integer length that is the sum of the minimum length of fiber required to connect the entire set of farms.

Sample Input:
4
0 4 9 21
4 0 8 17
9 8 0 16
21 17 16 0

Sample Output:
28

(1)利用优先队列优化的prim算法求解
此处主要介绍优先队列，其他细节与prim算法无太大差别
首先声明二元组，前者保存距离，后者保存编号

  1. typedef pair<int,int> pii;

声明一个变量名为q的优先队列，此处greater的优先级为小的距离先出队，也就实现了在O(logn)的时间复杂度内找寻最小距离的功能。

  1. priority_queue<pii,vector<pii>,greater<pii> > q;

核心程序

  1. while (!q.empty())
  2.  {
  3.     pii t = q.top();q.pop();
  5.     int x = t.second;
  7.     if (vis[x]) continue;//点已经加入V，直接找下一个点
  9.     ans += d[x];
  11.     vis[x] = 1;
  13.     for (int i = 0;i < g[x].size();i++)
  14.     {
  15.       int y = g[x][i];
  17.       if (mp[x][y] < d[y])
  18.       {
  19.         d[y] = mp[x][y];
  20.         q.push(pii(d[y],y));//因为pair的默认优先级是先判断第一个元素，再判断第二个元素，所以二元组的一个元素是距离
  21.       }
  22.     }
  23.   }

(2)具体步骤（节点编号 0 - 3）
原图
第一步，把0点加入，并把与0点相连的边(4,1),(9,2),(21,3)入队，把0标记为已访问。

一图
第二步，最小是边4，把1点加入最小生成树，并把(8,2),(17,3)入队，把1标记为访问。

二图
第三步，最小是8，把2点加入最小生成树，并把(16,3)入队。

三图
第四步，最小是9，但是2已经被访问，继续循环。
最小是16，把3加入最小生成树。

自此，所有的点已经加入最下生成树。

经检验，正确，结果为28.

提交结果：优先队列优化prim

*具体代码见附录

四、实验结果分析

　 　最小生成树中不能有环，因此在三种算法中，都成功去除了可能会连接成环的边。实验的结果在第三点对实际问题求解中都有体现，我们也对多组数据进行验证过，均能够找出最小生成树。

五、实验总结

　　我们运用了多种算法并通过求解实际问题来实现找到最小生成树，其中考虑到时间复杂度，我们还对Prim算法进行了优化。考虑的情况较多所以编程时更要考虑周到，在编写程序的过程中不断调试也使我们对这几个算法有了更深刻的理解和认识，也基本掌握了如何用这几个算法求解实际问题。
　　作为计科学子，我们应该有利用计算机解决实际问题的能力，本次实验让我们对运用专业知识解决实际应用问题有了一定的理解和经验，也使我们对算法有了更深入的认识。让我们学到如何将一些现实的问题转换成我们能够实现的代码。

六、附录

姓名 涂麟子 刘妍 秦锐锋
主要负责 程序及资料收集 论文写作 算法及模型

Kruskal算法求解

  1. #include <stdio.h>
  2. #include <string.h>
  3. #include <algorithm>
  4. using namespace std;
  6. int mp[30][30];
  7. const int inf = 0x3f3f3f3f;
  9. int par[30];
  11. struct road
  12. {
  13.     int from,to;
  14.     int len;
  15. }e[80];
  17. bool cmp(struct road a,struct road b)
  18. {
  19.     return a.len < b.len;
  20. }
  22. void init(void)
  23. {
  24.     for (int i = 0;i < 30;i++)
  25.         par[i] = i;
  26. }
  28. int fin(int x)
  29. {
  30.     if (par[x] == x)
  31.         return x;
  32.     else
  33.         return par[x] = fin(par[x]);
  34. }
  36. bool unite(int x,int y)
  37. {
  38.     x = fin(x);
  39.     y = fin(y);
  41.     if (x == y) return false;
  43.     par[y] = x;
  45.     return true;
  46. }
  48. int main()
  49. {
  50.     int n;
  52.     while (scanf("%d",&n) != EOF)
  53.     {
  54.         memset(e,0,sizeof(e));
  56.         init();
  58.         if (!n) break;
  60.         //memset(mp,inf,sizeof(inf));
  62.         int cnt = 0;
  64.         for (int i = 0;i < n - 1;i++)
  65.         {
  66.             char s[5];
  68.             scanf("%s",s);
  70.             //printf("%s*\n",s);
  72.             int k;
  74.             scanf("%d",&k);
  76.             for (int j = 0;j < k;j++)
  77.             {
  78.                 char t[5];
  79.                 int tt;
  80.                 scanf("%s %d",t,&tt);
  82.                 //printf("%s*\n",t);
  84.                 e[cnt].from = s[0] - 'A';
  85.                 e[cnt].to = t[0] - 'A';
  86.                 e[cnt].len = tt;
  88.                 cnt++;
  89.             }
  90.         }
  92.         sort(e,e+cnt,cmp);
  94.         int edge = 0;
  96.         int ans = 0;
  98.         for (int i = 0;i < cnt;i++)
  99.         {
  100.             int x = e[i].from,y = e[i].to;
  102.             if (!unite(x,y)) continue;
  104.             ans += e[i].len;
  106.             edge++;
  108.             if (edge == n) break;
  109.         }
  111.         printf("%d\n",ans);
  112.     }
  114.     return 0;
  115. }

破圈法求解

  1. #include <stdio.h>
  2. #include <string.h>
  3. #include <algorithm>
  4. using namespace std;
  6. bool mp[30][30];
  7. bool v[30];
  8. int n;
  10. struct road
  11. {
  12.     int from,to;
  13.     int len;
  14. }e[80];
  16. int num = 0;
  18. void dfs(int x)
  19. {
  20.     v[x] = 1;
  22.     num++;
  24.     for (int i = 0;i < n;i++)
  25.     {
  26.         if (!v[i] && mp[x][i])
  27.         {
  28.             dfs(i);
  29.         }
  30.     }
  31. }
  33. bool cmp(struct road a,struct road b)
  34. {
  35.     return a.len < b.len;
  36. }
  39. int main()
  40. {
  41.     while (scanf("%d",&n) != EOF)
  42.     {
  43.         memset(e,0,sizeof(e));
  44.         memset(mp,0,sizeof(mp));
  46.         if (!n) break;
  48.         int cnt = 0;
  49.         long long ans = 0;
  51.         for (int i = 0;i < n - 1;i++)
  52.         {
  53.             char s[5];
  55.             scanf("%s",s);
  57.             //printf("%s*\n",s);
  59.             int k;
  61.             scanf("%d",&k);
  65.             for (int j = 0;j < k;j++)
  66.             {
  67.                 char t[5];
  68.                 int tt;
  69.                 scanf("%s %d",t,&tt);
  71.                 //printf("%s*\n",t);
  73.                 e[cnt].from = s[0] - 'A';
  74.                 e[cnt].to = t[0] - 'A';
  75.                 e[cnt].len = tt;
  77.                 mp[e[cnt].from][e[cnt].to] = mp[e[cnt].to][e[cnt].from] = 1;
  79.                 ans += tt;
  81.                 cnt++;
  82.             }
  83.         }
  85.         sort(e,e+cnt,cmp);
  87.         /*for (int i = 1;i <= n;i++)
  88.         {
  89.             for (int j = 1;j <= n;j++) printf("%d ",mp[i][j]);
  91.             printf("\n");
  92.         }*/
  95.         int edge = cnt;
  97.         for (int i = cnt - 1;i >= 0;i--)
  98.         {
  99.             num = 0;
  101.             memset(v,0,sizeof(v));
  103.             int x = e[i].from,y = e[i].to;
  105.             mp[x][y] = mp[y][x] = 0;
  107.             dfs(0);
  109.             if (num == n)
  110.             {
  111.                 ans -= e[i].len;
  112.                 edge--;
  113.             }
  114.             else mp[x][y] = mp[y][x] = 1;
  115.         }
  117.         printf("%d\n",ans);
  120.     }
  122.     return 0;
  123. }

prime算法求解

  1. #include <stdio.h>
  2. #include <string.h>
  4. const int inf = 0x3f3f3f3f;
  6. int lowcost[30];
  7. int closest[30];
  8. int mp[30][30];
  9. int n;
  11. int prim(int v)
  12. {
  13.   int mindis,minone;
  15.   int ans = 0;
  17.   for (int i = 0;i < n;i++)
  18.   {
  19.     lowcost[i] = mp[v][i];
  20.   }
  22.   for (int i = 0;i < n - 1;i++)
  23.   {
  24.     mindis = inf;
  26.     for (int j = 0;j < n;j++)
  27.     {
  28.       if (lowcost[j] && mindis > lowcost[j])
  29.       {
  30.         mindis = lowcost[j];
  31.         minone = j;
  32.       }
  33.     }
  35.     ans += lowcost[minone];
  37.     lowcost[minone] = 0;
  39.     for (int j = 0;j < n;j++)
  40.     {
  41.       if (mp[j][minone] < lowcost[j])
  42.       {
  43.         lowcost[j] = mp[j][minone];
  44.       }
  45.     }
  46.   }
  48.   return ans;
  49. }
  51. int main()
  52. {
  53.   while (scanf("%d",&n) == 1 && n)
  54.   {
  55.     memset(lowcost,0,sizeof(lowcost));
  56.     memset(closest,0,sizeof(closest));
  57.     memset(mp,inf,sizeof(mp));
  59.     for (int i = 0;i < n;i++)
  60.     mp[i][i] = 0;
  62.     for (int i = 0;i < n - 1;i++)
  63.     {
  64.       char a[5];
  65.       int num;
  67.       scanf("%s",a);
  69.       scanf(" %d",&num);
  71.       for (int j = 0;j < num;j++)
  72.       {
  73.         char b[5];
  74.         int d;
  76.         scanf("%s",b);
  77.         scanf(" %d",&d);
  79.         int st = a[0] - 'A',en = b[0] - 'A';
  81.         mp[st][en] = mp[en][st] = d;
  82.       }
  83.     }
  85.     int ans = prim(0);
  87.     printf("%d\n",ans);
  88.   }
  91.   return 0;
  92. }

prime算法优化

  1. #include <stdio.h>
  2. #include <string.h>
  4. const int inf = 0x3f3f3f3f;
  6. int lowcost[30];
  7. int closest[30];
  8. int mp[30][30];
  9. int n;
  11. int prim(int v)
  12. {
  13.   int mindis,minone;
  15.   int ans = 0;
  17.   for (int i = 0;i < n;i++)
  18.   {
  19.     lowcost[i] = mp[v][i];
  20.   }
  22.   for (int i = 0;i < n - 1;i++)
  23.   {
  24.     mindis = inf;
  26.     for (int j = 0;j < n;j++)
  27.     {
  28.       if (lowcost[j] && mindis > lowcost[j])
  29.       {
  30.         mindis = lowcost[j];
  31.         minone = j;
  32.       }
  33.     }
  35.     ans += lowcost[minone];
  37.     lowcost[minone] = 0;
  39.     for (int j = 0;j < n;j++)
  40.     {
  41.       if (mp[j][minone] < lowcost[j])
  42.       {
  43.         lowcost[j] = mp[j][minone];
  44.       }
  45.     }
  46.   }
  48.   return ans;
  49. }
  51. int main()
  52. {
  53.   while (scanf("%d",&n) == 1 && n)
  54.   {
  55.     memset(lowcost,0,sizeof(lowcost));
  56.     memset(closest,0,sizeof(closest));
  57.     memset(mp,inf,sizeof(mp));
  59.     for (int i = 0;i < n;i++)
  60.     mp[i][i] = 0;
  62.     for (int i = 0;i < n - 1;i++)
  63.     {
  64.       char a[5];
  65.       int num;
  67.       scanf("%s",a);
  69.       scanf(" %d",&num);
  71.       for (int j = 0;j < num;j++)
  72.       {
  73.         char b[5];
  74.         int d;
  76.         scanf("%s",b);
  77.         scanf(" %d",&d);
  79.         int st = a[0] - 'A',en = b[0] - 'A';
  81.         mp[st][en] = mp[en][st] = d;
  82.       }
  83.     }
  85.     int ans = prim(0);
  87.     printf("%d\n",ans);
  88.   }
  91.   return 0;
  92. }

【1】孙小军 基于Prim算法的度约束最小生成树问题研究 中文核心期刊 2016 04 445-448
【2】黄坤 基于Kruskal算法的最小生成树的构建 ISSN：1009-3044 2010 23 6478-6481
【3】龙亚 破圈法构造最小生成树算法探讨 ISSN：1673-7059 2007 04 108-111
【4】江波、张黎 基于Prim算法的最小生成树优化研究 ISSN：1000-7024 2009 13 3244-3247

添加新批注
在作者公开此批注前，只有你和作者可见。
回复批注