【算法日积月累】15-并查集

并查集 路径压缩

“并查集”这部分知识点讲得最清楚的是《算法》（第 4 版）

以下是我的学习笔记。

什么是“并查集”

为什么叫并查集呢？因为在这个数据结构中，“并”和“查”是经常使用的两个操作。“并”是把两个元素合并在一起，仅表示“这两个元素之间有连接”，“查”就是查询两个元素是不是连接在一起。因此，如果我们在一些场景下，只需要查询两个事物之间是否有联系，“并查集”就是一个不错的选择。例如：“查询两个人是不是好友关系”（请看下面的练习1）。“查询从一个地方到另一个地方是否能走通”（请看下面的练习2）。

并查集主要用于解决连通问题，即抽象概念中结点和结点是否连接。而路径问题，不仅仅要考虑连通问题，我们还要往往还需要求出最短路径，这不是并查集做的事情。因此并查集问题能做的事情比路径问题少，它更专注于（1）判断连接状态（查）（2）改变连接状态（并）。

具体说来，并查集的代码需要实现以下的 3 个功能：

1、 find(p)：查找元素 p 所对应的集合，

说明：这个函数一般不对外开放，仅作为私有方法被下面两个函数调用。

2、 union(p, q)：合并元素 p 和元素 q 所在的集合。
3、 connected(p, q)：查询元素 p 和元素 q 是不是在同一个集合中。

因此，我们的并查集其实就是要实现下面的这个接口：

public interface IUnionFind {
    // 并查集的版本名称，由开发者指定
    String versionName();
    // p (0 到 N-1)所在的分量的标识符
    int find(int p);
    // 如果 p 和 q 存在于同一分量中则返回 true
    boolean connected(int p, int q);
    // 在 p 与 q 之间添加一条连接
    void union(int p, int q);
}

在后面我们会看到，其实“并查集”是一棵树，这棵树与以往我们构建树的方式大不相同，“并查集”构建的树从“孩子结点”指向“父亲结点”。这一点是“并查集”的特色。

并查集第 1 版：quick-find

我们首先解决并查集用什么数据结构来表示呢？其实使用数组就可以了，这个数组我们可以起一个名字叫做 id 。初始化的情况下，每一个元素的 id 都是不一样的。如果是一样的，表示是属于同一个集合内的元素。

基于 id 的 quick-find 的思路：设置 id 数组，数组的每个元素是分量标识。

从 quick-find 这个名字上看，我们这一版的实现，对于 find(int p) 这个操作来说是高效的，但对于 union(int p, int q) 这个操作是低效的，因为需要遍历整个并查集。find(int p) 这个操作的时间复杂度是 $O(1)$，而 union(int p, int q) 这个操作的时间复杂度是 $O(n)$，要全部遍历并查集中的元素，把其中一个分量标识的所有结点的编号更改为另一个一个分量标识。


例如上面的表格中，如果我们要将第 1 行的 0 和 1 执行 union(int p, int q) 操作，有两种方式：第 1 种方式：把第 1 行的 0，2，4，6，8 的 id 全改成 1；第 2 种方式：把第 1 行的 1，3，5，7，9 的 id 全改成 0。我们可以看到，union(int p, int q) 的操作完全是和问题的规模成正比的，所以 quick-find 下的 union(int p, int q) 操作时间复杂度是 $O(n)$。

public class UnionFind1 implements IUnionFind {
    private int[] id; // 分量 id
    private int count; // 联通分量的数量
    public UnionFind1(int n) {
        this.count = n;
        // 初始化分量 id 数组
        id = new int[n];
        for (int i = 0; i < n; i++) {
            id[i] = i;
        }
    }
    @Override
    public String versionName() {
        return "并查集的第 1 个版本，基于 id 数组，quick-find";
    }
    // 以常数时间复杂度，返回分量的标识符，与并查集的规模是无关的，这一步很快
    // 因此我们称这个版本的并查集是 quick-find
    @Override
    public int find(int p) {
        return id[p];
    }
    @Override
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }
    // 因为需要遍历数组中的全部元素，所以其实这个版本效率并不高
    @Override
    public void union(int p, int q) {
        int pid = find(p);
        int qid = find(q);
        // 如果 p 和 q 已经在相同的分量之中，则什么都不做
        if (pid == qid) {
            return;
        }
        // 将 p 的分量重新命名为 q 的名称
        for (int i = 0; i < id.length; i++) {
            if (find(i) == pid) {
                id[i] = qid;
            }
        }
        // 每次 union 以后，连通分量减 1
        count--;
    }
}

使用 id 数组在进行 union(int p, int q) 的时候，要遍历整个数组中的结点，这种方式效率不高，因此，我们换一种思路：由于 union(int p, int q) 慢，所以我们就想办法让 union(int p, int q) 快起来。

并查集第 2 版：quick-union

我们不再使用 id 数组，而使用 parent 数组，parent 数组的定义是：parent[i] 表示索引为 i 这个结点的父亲结点的索引，在这样的定义下，根结点的父亲结点是自己。

此时查询结点 p 和结点 q 相连这件事情，就是我们分别追溯 parent[p] 和 parent[q] （可以看到这样的过程很像在一棵树中的操作），查询到 parent[p] 和 parent[q] 的根结点，如果根结点相同，那么它们就同属于一个集合。

这样看来，find(int p) 好像费点劲，这也是我们接来下的几个并查集优化的方向，都是在 find(int p) 上做文章，但这保证了 union(int p, int q) 很快，我们只需把其中一个结点的父结点指向另一个结点的根结点（而谁的父结点指向谁的根结点，也是我们后几版并查集优化的方向），就完成了 union(int p, int q) 的操作。此时 union(int p, int q) 的操作只须要一行代码：

parent[pRoot] = qRoot;

初始化的时候，我们将每个元素都指向自己，此时表示这 $10$ 个结点互相之间没有连接关系。如下表所示：

上面的数组表示的并查集如下。

从正确性上来说，谁的根指向谁的根都是可以的。但是在实际运行的时候，我们会发现，我们应该将层级较少的根指向层级较多的根，这样做是为了保证我们的并查集形成的树的高度不会增加，这样在 find 的时候，追溯的层数不会增加。我们在查找根的时候，应该使得查找的层数最少。

public class UnionFind2 implements IUnionFind {
    private int[] parent; // 第 i 个元素存放它的父元素的索引
    private int count; // 联通分量的数量
    public UnionFind2(int n) {
        this.count = n;
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }
    @Override
    public String versionName() {
        return "并查集的第 2 个版本，基于 parent 数组，quick-union";
    }
    @Override
    public int find(int p) {
        // 跟随链接找到根结点
        while (parent[p] != p) { // 只要不是根结点
            p = parent[p];
        }
        return p;
    }
    @Override
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }
    @Override
    public void union(int p, int q) {
        int pRoot = find(p); // 将 p 归并与之相同的分量中
        int qRoot = find(q); // 将 q 归并与之相同的分量中
        // 如果 p 和 q 已经在相同的分量之中，则什么都不做
        if (pRoot == qRoot) {
            return;
        }
        // 如果 parent[qRoot] = pRoot; 也是可以的，即将其中一个结点指向另一个结点
        parent[pRoot] = qRoot;
        // 每次 union 以后，连通分量减 1
        count--;
    }
}

并查集第 3 版：quick-union 基于 size 的优化

我们发现 union 4,9 与 union 9,4 其实是一样的，也就是把谁的根指向谁的根，这一点从正确性上来说是无关紧要的，但是对于 find 的时间复杂度就会有影响。为此，我们做如下优化。

在合并之前做判断，具体做法是，计算每一个结点有多少个元素直接或者间接地以它为根，我们应该将集合元素少的那结点的根指向集合元素多的那个结点的根。这样，形成的树就会更高概率地形成一棵层数较低的树。

为此，我们再引入一个 size 数组，size[i] 的定义是：以第 i 个结点为根的集合的元素的个数。

在初始化的时候 size[i] = 1，find 和 isConnected 操作中我们都不须要去维护 size 这个数组，唯独在 unionElements 的时候，我们才要维护 size 数组的定义。

// union-find 算法的实现（加权 quick-union 算法）
public class UnionFind3 implements IUnionFind {
    private int[] parent; // 第 i 个元素存放它的父元素的索引
    private int count; // 联通分量的数量
    private int[] size; // 以当前索引为根的树所包含的元素的总数
    public UnionFind3(int n) {
        this.count = n;
        parent = new int[n];
        size = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            // 初始化时，所有的元素只包含它自己，只有一个元素，所以 size[i] = 1
            size[i] = 1;
        }
    }
    @Override
    public String versionName() {
        return "并查集的第 3 个版本，基于 parent 数组，quick-union，基于 size";
    }
    // 返回索引为 p 的元素的根结点的索引
    @Override
    public int find(int p) {
        // 跟随链接找到根结点
        while (p != parent[p]) {
            p = parent[p];
        }
        return p;
    }
    @Override
    public boolean connected(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        return pRoot == qRoot;
    }
    @Override
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot == qRoot) {
            return;
        }
        // 这一步是与第 2 版不同的地方，我们不是没有根据地把一个结点的根结点的父结点指向另一个结点的根结点
        // 而是将小树的根结点连接到大树的根结点
        if (size[pRoot] > size[qRoot]) {
            parent[qRoot] = pRoot;
            size[pRoot] += size[qRoot];
        } else {
            parent[pRoot] = qRoot;
            size[qRoot] += size[pRoot];
        }
        // 每次 union 以后，连通分量减 1
        count--;
    }
}

并查集第 4 版：quick-union 基于 rank 的优化

使用 size 来决定将哪个结点的根指向另一个结点的根，其实并不太合理，但并不能说不正确，因为谁的根指向谁的根，其实都没有错，下面就是一个特殊的情况。


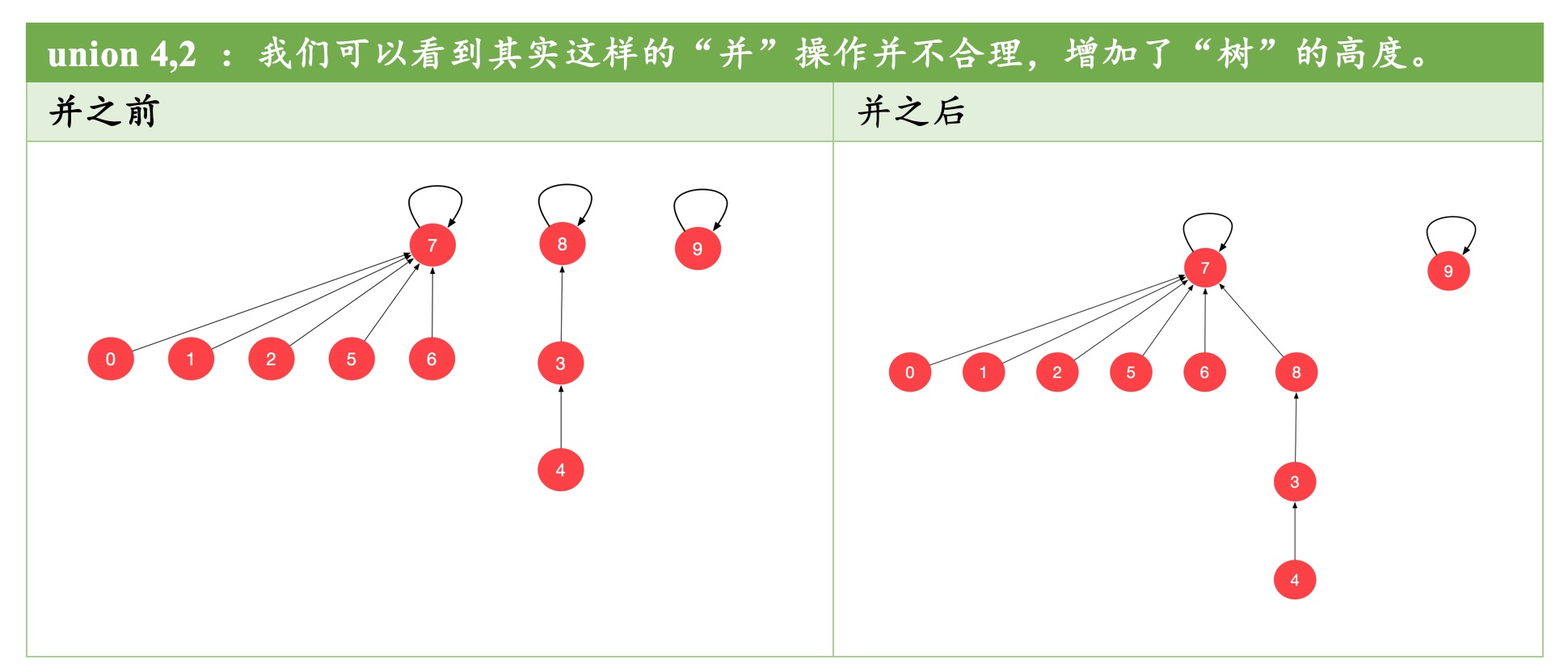
因为我们总是期望这棵树的高度比较低，在这种情况下，我们在 find 的时候，就能通过很少的步数来找到根结点，进而提高 find 的效率。为此，我们引入 rank 数组，其定义是： rank[i] 表示以第 i 个元素为根的树的高度。

public class UnionFind4 implements IUnionFind {
    private int[] parent;
    private int count;
    // 以索引为 i 的元素为根结点的树的深度（最深的那个深度）
    private int[] rank;
    public UnionFind4(int n) {
        this.count = n;
        parent = new int[n];
        rank = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            // 初始化时，所有的元素只包含它自己，只有一个元素，所以 rank[i] = 1
            rank[i] = 1;
        }
    }
    @Override
    public String versionName() {
        return "并查集的第 4 个版本，基于 parent 数组，quick-union，基于 rank";
    }
    // 返回索引为 p 的元素的根结点
    @Override
    public int find(int p) {
        // 跟随链接找到根结点
        while (p != parent[p]) {
            p = parent[p];
        }
        return p;
    }
    @Override
    public boolean connected(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        return pRoot == qRoot;
    }
    @Override
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot == qRoot) {
            return;
        }
        // 这一步是与第 3 版不同的地方
        if (rank[pRoot] > rank[qRoot]) {
            parent[qRoot] = pRoot;
        } else if (rank[pRoot] < rank[qRoot]) {
            parent[pRoot] = qRoot;
        } else {
            parent[qRoot] = pRoot;
            rank[pRoot]++;
        }
        // 每次 union 以后，连通分量减 1
        count--;
    }
}

并查集第 5 版：quick-union 基于路径压缩的非递归实现

那么什么是路径压缩 path Compression？以上我们都是针对于 union 操作的优化，其实我们在 find 的时候，就可以对一棵树进行整理，让它的高度变低，这一点是基于并查集的一个特性：只要它们是连在一起的，其实谁指向谁，并不重要，所以我们在接下来的讨论中看到的并查集的表示图，它们是等价的，即它们表示的都是同一个并查集。

路径压缩 path Compression 的思路：在 find 的时候一次又一次的整理，将并查集构造（整理）成一个与之等价的并查集，使得后续的每一次 find 这样的操作路径最短。

假设一个最极端的并查集的图表示如下：

我们开始找 $4$ 的父亲结点，$4$ 的父亲结点不是 $4$ ，说明不是根结点，此时，我们尝试 $2$ 步一跳，将 $4$ 的父亲结点“改成”父亲结点的父亲结点，于是得到一个等价的并查集：

下面我们该考察元素 $2$ 了，$2$ 的父亲结点是 $1$，$2$ 不是根结点，所以我们继续两步一跳，把 $2$ 的父亲结点设置成它的父亲结点的父亲结点，于是又得到一个等价的并查集：

此时，整棵树的高度就在一次 find 的过程中被压缩了。

这里有一个疑问：即使我们在最后只差一步的情况下，我们跳两步，也不会出现无效的索引。其实，一步一跳，两步一跳，甚至三步一跳都没有关系。

画图画了这么多，代码实现起来只有一句：parent[p] = parent[parent[p]]; 编写的时候要注意这行代码添加的位置，画一个示意图，想想这个路径压缩的过程，不难写出。

public int find(int p) {
    // 在 find 的时候执行路径压缩
    while (p != parent[p]) {
        // 编写这句代码的时候可能会觉得有点绕，
        // 技巧是画一个示意图，就能很直观地写出正确的逻辑
        // 两步一跳完成路径压缩
        parent[p] = parent[parent[p]];
        p = parent[p];
    }
    return p;
}

根据上面的图，我们通过 find 操作执行路径压缩，最终形成的并查集如下：

并查集第 6 版：quick-union 基于路径压缩的递归实现

代码的实现的理解有一些绕。这一版我们实现压缩更彻底的路径压缩。其实我们不看上面的分析，我们想象路径压缩的目的是什么，就是让我们的并查集表示的树结构层数更低，那么最优的情况应该是下面这样，把一棵树压缩成 $2$ 层，所有的结点都指向一个根，这才是把一个并查集压缩到最彻底的情况。

那么，代码又应该如何实现呢？我们需要使用递归的思想。这一版代码的实现难点就在于：应该定义 find(p) 返回的是 p 这个结点的父结点。

/**
 * 返回索引为 p 的元素的根结点
 * 理解这个方法的关键点：我们就是要把这个结点的父结点指向根结点，
 * 既然父亲结点不是根结点，我们就继续拿父亲结点找根结点
 * 一致递归找下去，
 * 最后返回的时候，写 parent[p] 是可以的
 * 写 parent[parent[p]] 也是没有问题的
 *
 * @param p
 * @return
 */
public int find(int p) {
    // 在 find 的时候执行路径压缩
    assert p >= 0 && p < count;
    // 注意：这里是 if 不是 while，否则就变成循环
    if (p != parent[p]) {
        // 这一行代码的逻辑要想想清楚
        // 只要不是根结点
        // 就把父亲结点指向父亲结点的父亲结点
        parent[p] = find(parent[p]);
    }
    return parent[p];
}

最后，我们来比较一下基于路径压缩的两种方法。

并查集能够很好地帮助我们解决网络中两个结点是否连接的问题。但是，对于网络中的两个结点的路径，最短路径的问题，我们就要使用图来解决。

关于路径压缩的思考

写到这里，我们发现在路径压缩的过程中，我们之前引入的辅助合并的数组，不管是 rank 还是 size，它们的定义都不准确了，因为我们在路径压缩的过程中没有对它们的定义进行维护。这一点其实并不影响我们的算法的正确性，我们不去维护 rank 数组和 size 数组的定义，是因为第 1 点，难于实现，第 2 点 rank 数组还是 size 数组的当前实现仍然可以作为一个参考值，比起随机的做法要更有意义一些。

其实写到这里，数组 rank 还是数组 size 都不太重要了，我们只用在 find 的时候，做好路径压缩，把孩子结点指向父亲结点即可。

并查集第 7 版：易于理解的路径压缩算法

Python 实现：

class UnionFind7:
    def __init__(self, n):
        self.parent = [i for i in range(n)]
        self.count = n
    def find(self, p):
        """
        查找元素 p 根节点的编号
        :param p:
        :return:
        """
        assert 0 <= p < self.count
        root = p
        while root != self.parent[root]:
            root = self.parent[root]
        # 此时 root 就是大 boss
        # 下面这一步就是最直接的路径压缩：
        # 把沿途查找过的结点都指向 root
        while p != self.parent[p]:
            temp = self.parent[p]
            self.parent[p] = root
            p = temp
        return root
    def is_connected(self, p, q):
        """
        查询元素 p 和 q 是否属于同一个集合
        有共同的父亲，就表示它们属于同一个集合
        :param p:
        :param q:
        :return:
        """
        return self.find(p) == self.find(q)
    def union(self, p, q):
        """
        合并元素 p 和元素 q 所属于的集合
        O(n)复杂度
        :param p:
        :param q:
        :return:
        """
        p_id = self.find(p)
        q_id = self.find(q)
        if p_id == q_id:
            return
        # 任意指向即可
        self.parent[p_id] = q_id

下面，我们来看 LeetCode 上关于“并查集”的两个问题。

例题

例题1：LeetCode 第 547 题：朋友圈

传送门：547. Friend Circles、547. 朋友圈。

要求：班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。

给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。

示例 1:

输入: 
[[1,1,0],
 [1,1,0],
 [0,0,1]]
输出: 2 
说明：已知学生0和学生1互为朋友，他们在一个朋友圈。
第2个学生自己在一个朋友圈。所以返回2。

示例 2:

输入: 
[[1,1,0],
 [1,1,1],
 [0,1,1]]
输出: 1
说明：已知学生0和学生1互为朋友，学生1和学生2互为朋友，所以学生0和学生2也是朋友，所以他们三个在一个朋友圈，返回1。

注意：

1. N 在[1,200]的范围内。
2. 对于所有学生，有M[i][i] = 1。
3. 如果有M[i][j] = 1，则有M[j][i] = 1。

分析：好友关系是双向关系，因此题目中给出的矩阵就是一个邻接矩阵。所以问题就转化为求图中有几个连通分量的问题了，这是思路1。

我们还可以用并查集的思路来考虑它。因为是对阵矩阵，我们其实只要看这个矩阵的下三角形部分（可以不看对角线，因为自己肯定是自己的好友）就可以了。

Python 代码：

class Solution(object):
    def findCircleNum(self, M):
        """
        :type M: List[List[int]]
        :rtype: int
        """
        class UnionFind:
            def __init__(self, n):
                self.parent = [i for i in range(n)]
            def find(self, p):
                root = p
                # 只要不是最上层的那个结点，就不停向上找
                while root != self.parent[root]:
                    root = self.parent[root]
                # 此时 root 就是大 boss
                # 接下来把 p 到 root 沿途所有的结点都指向 root
                while p != self.parent[p]:
                    temp = self.parent[p]
                    self.parent[p] = root
                    p = temp
                return root
            def is_connected(self, p, q):
                return self.find(p) == self.find(q)
            def union(self, p, q):
                p_id = self.find(p)
                q_id = self.find(q)
                if p_id == q_id:
                    return
                self.parent[p_id] = q_id
        m = len(M)
        union_find_set = UnionFind(m)
        # 只看下三角矩阵(不包括对角线)
        for i in range(m):
            for j in range(i):
                if M[i][j] == 1:
                    union_find_set.union(j, i)
        counter = 0
        # print(union_find_set.parent)
        # 自己的父亲是自己的话，这个结点就是根结点，是老大，是 boss
        # boss 的特点就是，他上面没有人，例如：李彦宏、马云
        # 数一数有几个老大，就有几个朋友圈
        for index, parent in enumerate(union_find_set.parent):
            if index == parent:
                counter += 1
        return counter
if __name__ == '__main__':
    M = [[1, 1, 0],
         [1, 1, 0],
         [0, 0, 1]]
    solution = Solution()
    result = solution.findCircleNum(M)
    print(result)

例题2：LeetCode 第 130 题：被围绕的区域

传送门：200. Number of Islands、200. 岛屿的个数。

给定一个二维的矩阵，包含 'X' 和 'O'（字母 O）。

找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例:

X X X X
X O O X
X X O X
X O X X

运行你的函数后，矩阵变为：

X X X X
X X X X
X X X X
X O X X

解释:

被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

分析：其实就是将不与边上的 'O' 相连的 'O' 改成 'X'，可以使用并查集完成。

Python 版本1：（一开始的写法，不太好理解）。

class Solution:
    def solve(self, board):
        """
        :type board: List[List[str]]
        :rtype: void Do not return anything, modify board in-place instead.
        """
        # 使用并查集
        class UnionFind:
            def __init__(self, n):
                self.parent = [i for i in range(n)]
            def find(self, p):
                root = p
                while root != self.parent[root]:
                    root = self.parent[root]
                while p != self.parent[p]:
                    temp = self.parent[p]
                    self.parent[p] = root
                    p = temp
                return root
            def is_connected(self, p, q):
                return self.find(p) == self.find(q)
            def union(self, p, q):
                p_id = self.find(p)
                q_id = self.find(q)
                if p_id == q_id:
                    return
                self.parent[p_id] = q_id
        # 一开始是常规的代码
        m = len(board)
        if m == 0:
            return
        n = len(board[0])
        def get_index(x, y):
            return x * n + y
        directions = [(-1, 0), (0, -1), (1, 0), (0, 1)]
        # 这里多留了一个位置，表示与边上的 'O' 相连
        uf = UnionFind(m * n + 1)
        for i in range(m):
            for j in range(n):
                if board[i][j] == 'O':
                    # 把所有不被 'X' 包围的 'O' 放在同一个集合里
                    if i == 0 or j == 0 or i == m - 1 or j == n - 1:
                        uf.union(get_index(i, j), m * n)
                    else:
                        # 向 4 个方向找，只用看 4 个方向，不要和回溯算法混淆了
                        # 只要都是 'O' ，才有必要合并
                        for direction in directions:
                            new_i = i + direction[0]
                            new_j = j + direction[1]
                            if board[new_i][new_j] == 'O':
                                uf.union(get_index(i, j), get_index(new_i, new_j))
        # 最后，才内圈里，只要是 'O'，且不与边上的 'O' 连接，都改成 'X' 即可  
        for i in range(1, m - 1):
            for j in range(1, n - 1):
                if board[i][j] == 'O' and not uf.is_connected(get_index(i, j), m * n):
                    board[i][j] = 'X'

这个版本写出来，感觉思路不是很清晰，于是，我又写了一版。

Python 第 2 版：其实并查集的写法容易受 floorfill 的影响，用并查集的时候，只用每一行的右边和下面都看一下，只针对“O”，能合并就合并一下。

class Solution:
    def solve(self, board):
        """
        :type board: List[List[str]]
        :rtype: void Do not return anything, modify board in-place instead.
        """
        # 使用并查集
        class UnionFind:
            def __init__(self, n):
                self.parent = [i for i in range(n)]
            def find(self, p):
                root = p
                while root != self.parent[root]:
                    root = self.parent[root]
                while p != self.parent[p]:
                    temp = self.parent[p]
                    self.parent[p] = root
                    p = temp
                return root
            def is_connected(self, p, q):
                return self.find(p) == self.find(q)
            def union(self, p, q):
                p_id = self.find(p)
                q_id = self.find(q)
                if p_id == q_id:
                    return
                self.parent[p_id] = q_id
        # 一开始是常规的代码
        m = len(board)
        if m == 0:
            return
        n = len(board[0])
        def get_index(x, y):
            return x * n + y
        dummy_node = m * n
        uf = UnionFind(m * n + 1)
        # 先把四条边上的 "O" 全部连起来
        for row_index in range(m):
            if board[row_index][0] == 'O':
                uf.union(get_index(row_index, 0), dummy_node)
            if board[row_index][n - 1] == 'O':
                uf.union(get_index(row_index, n - 1), dummy_node)
        for col_index in range(n):
            if board[0][col_index] == 'O':
                uf.union(get_index(0, col_index), dummy_node)
            if board[m - 1][col_index] == 'O':
                uf.union(get_index(m - 1, col_index), dummy_node)
        directions = [(1, 0), (0, 1)]
        for i in range(m):
            for j in range(n):
                if board[i][j] == 'O':
                    # 只向 2 个方向找，只用看 2 个方向，不要和回溯算法混淆了
                    for direction in directions:
                        new_i = i + direction[0]
                        new_j = j + direction[1]
                        if new_i < m and new_j < n and board[new_i][new_j] == 'O':
                            uf.union(get_index(i, j), get_index(new_i, new_j))
        for i in range(1, m - 1):
            for j in range(1, n - 1):
                if board[i][j] == 'O' and not uf.is_connected(get_index(i, j), m * n):
                    board[i][j] = 'X'

练习3：LeetCode 第 200 题：岛屿的个数

给定一个由 '1'（陆地）和 '0'（水）组成的的二维网格，计算岛屿的数量。一个岛被水包围，并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。

示例 1:

输入:
11110
11010
11000
00000
输出: 1

示例 2:

输入:
11000
11000
00100
00011
输出: 3

Python 代码：

class Solution(object):
    def numIslands(self, grid):
        """
        :type grid: List[List[str]]
        :rtype: int
        """
        class UnionFind:
            def __init__(self, n):
                self.parent = [i for i in range(n)]
            def find(self, p):
                root = p
                while root != self.parent[root]:
                    root = self.parent[root]
                while p != self.parent[p]:
                    temp = self.parent[p]
                    self.parent[p] = root
                    p = temp
                return root
            def is_connected(self, p, q):
                return self.find(p) == self.find(q)
            def union(self, p, q):
                p_id = self.find(p)
                q_id = self.find(q)
                if p_id == q_id:
                    return
                self.parent[p_id] = q_id
        row = len(grid)
        if row == 0:
            return 0
        col = len(grid[0])
        def get_index(x, y):
            return x * col + y
        directions = [(1, 0), (0, 1)]
        # 多开一个空间，把 "0" 都归到这个虚拟的老大上
        dummy_node = row * col
        uf = UnionFind(dummy_node + 1)
        for i in range(row):
            for j in range(col):
                if grid[i][j] == '0':
                    uf.union(get_index(i, j), dummy_node)
                if grid[i][j] == '1':
                    # 向下向右如果都是 "1" 就要合并一下
                    for direction in directions:
                        new_x = i + direction[0]
                        new_y = j + direction[1]
                        if new_x < row and new_y < col and grid[new_x][new_y] == '1':
                            uf.union(get_index(i, j), get_index(new_x, new_y))
        # 因为一定要减掉 "0" 的区域，因此起始值是 -1
        res = -1
        for index, parent in enumerate(uf.parent):
            if parent == index:
                res += 1
        return res

（完）