红黑树

数据结构

阅读本文需要了解2-3树（实际上是一棵3阶B树），对于红黑树理解很有帮助
源码地址:https://github.com/huangyichun/DataStructure/tree/master/RB_Tree/src/main/java

定义:

• 红链接均为左链接
• 没有任何一个节点同时和两条红链接相连
• 该树是完美黑色平衡的，即任意空链接到根节点的路径上的黑链接数量相同

满足这样定义的红黑树和相应的2-3树是一一对应的。（2-3树是一颗3阶的B树，一个结点最多有2个Key，将左边的一个变成红黑树中的红色节点，就转换成红黑树了）

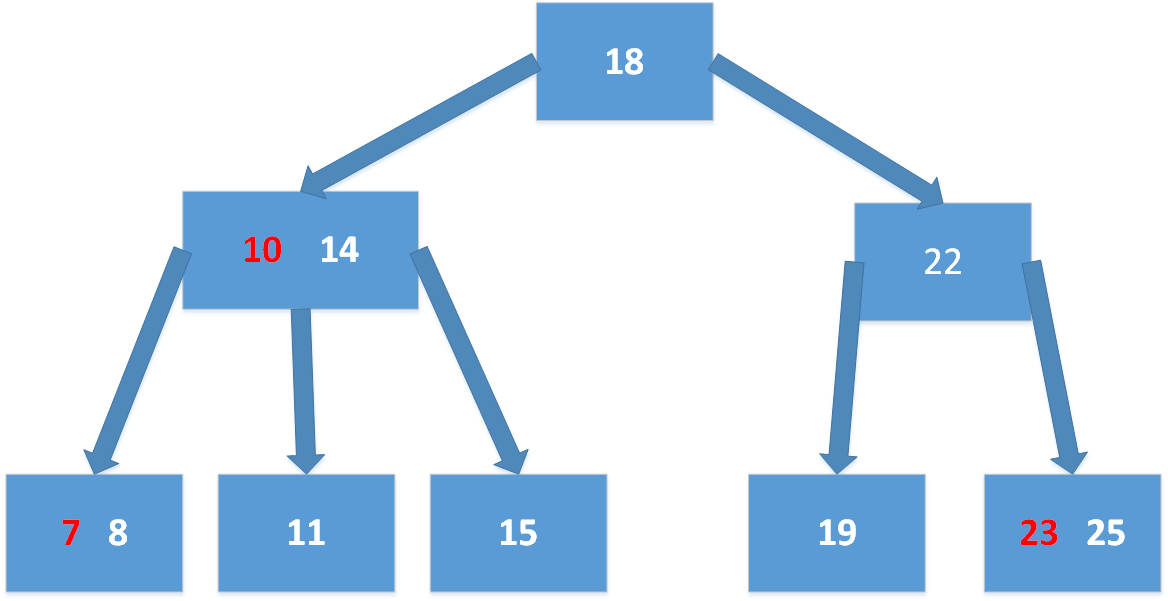
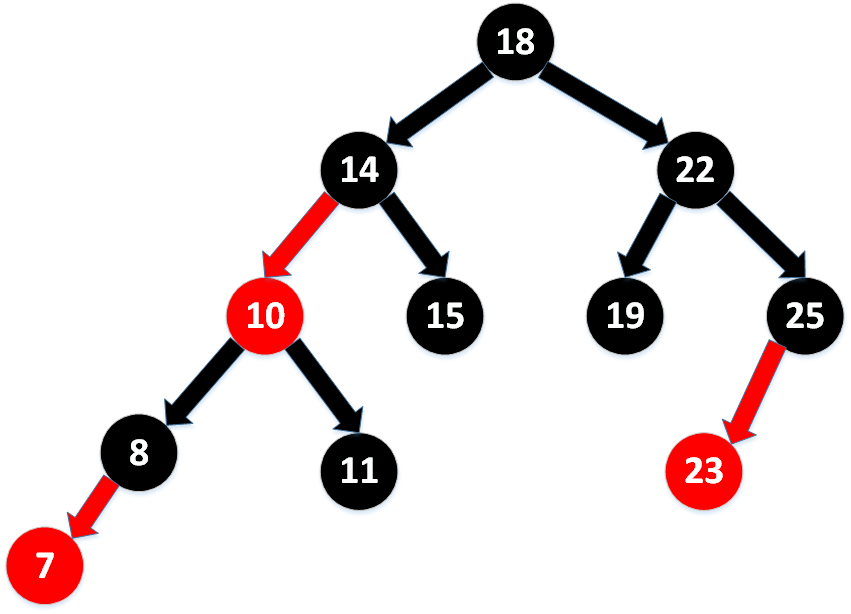
    因为每个节点都会只有一条指向自己的链接(从它的父节点指向它)，我们将链接的颜色保存在表示节点的Node数据类型的布尔变量color中。如果指向它的链接是红色的，那么该变量为true，黑色则为false。我们约定空连接为黑色。为了代码的清晰我么定义了两个常亮RED和BLACK来设置和测试这个变量。我们使用私有方法isRead()来测试一个节点和它的父节点之间的链接的颜色。

    /**
     * 红黑树
     */
    public class RBTree<Key extends Comparable<Key>, Value> {
        private static final boolean RED = true;
        private static final boolean BLACK = false;
        private class Node{
            Key key;    //键
            Value val;  //相关的值
            Node left ,right;   //左右子树
            int N;  //这棵子树的结点总数
            boolean color;  //由其父节点指向它的链接的颜色
            public Node(Key key, Value val, int n, boolean color) {
                this.key = key;
                this.val = val;
                N = n;
                this.color = color;
            }
        }
    }

红黑树旋转

在操作中可能会出现红色右链接或者两条连续的红链接，我们可以通过旋转修复。
左旋转: 将一条红色的右链接转换为左链接

     /**
         * 左旋转
         * @param h
         * @return
         */
        private Node rotateLeft(Node h){
            Node x = h.right;
            h.right = x.left;
            x.left = h;
            x.color = h.color;
            h.color = RED;
            x.N = h.N;
            h.N = size(h.left) + size(h.right) + 1;//修改节点个数
            return x;
        }

右旋转: 将一条红色的左链接转换为右链接

      /**
         * 右旋转
         * @param h
         * @return
         */
        private Node rotateRight(Node h){
            Node x = h.left;
            h.left = x.right;
            x.right = h;
            x.color = h.color;
            h.color = RED;
            x.N = h.N;
            h.N = size(h.left) + size(h.right) + 1;//修改节点个数
            return x;
        } 

插入:

• 向只有一个黑色节点的红黑树插入新键 :
  如果新键小于老键我们只需新增一个红色的节点即可。
  
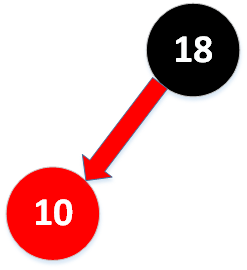
  如果新键大于老键，那么新增的红色结点将会产生一条红色的右链接。那么我们需要调用root = rotateLeft(root)；将其旋转为红色左链接并修正根节点的链接。
  
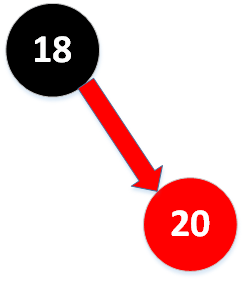
  旋转修正后:
  

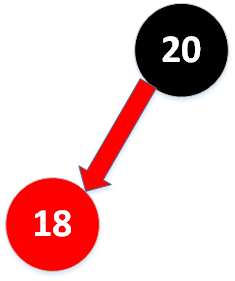
• 向底部的黑色节点插入新键（该节点已经没有子节点，2-节点）
  为了保证有序性，我们总是用红色链接将新节点和它的父节点相连。处理情况与上面的相同。

• 向一棵双键树中插入新键(即一个3-节点)有3中情况:

1. 新键小于树中的两个键

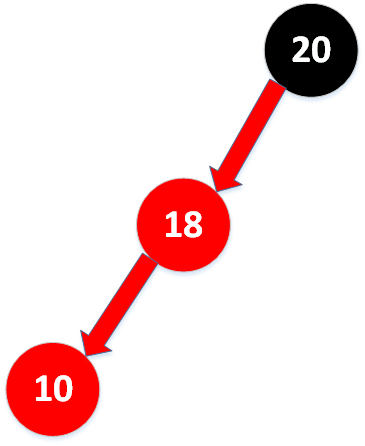
先进行右旋转:

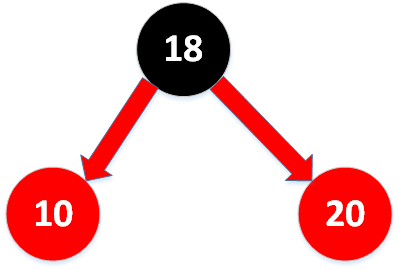
再将两个节点变为黑色:

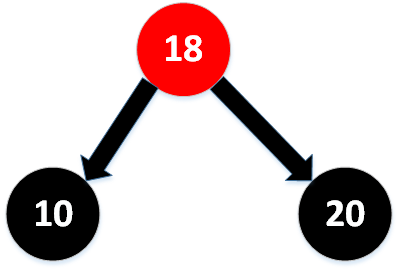
2. 新键在两者之间

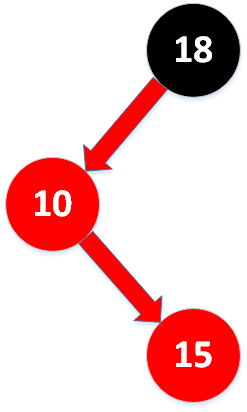
先进行左旋转:

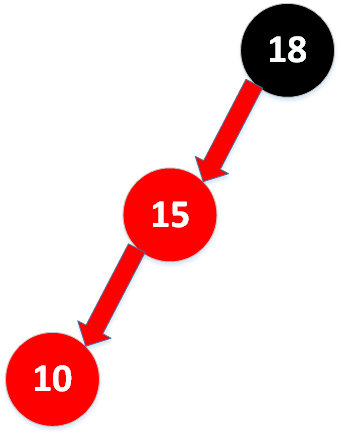
再根据上面的情况进行处理。

3. 新键大于树中的两个键

这种情况下:

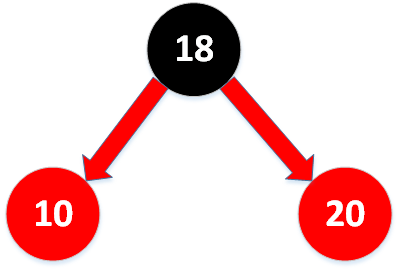
将两个节点变成黑色就可以了

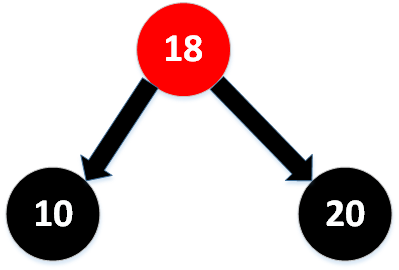
当我们将插入的结点变成3这种情况时，我们需要一个函数将一个节点的两个红色子节点的颜色变为黑色。父节点变为红色。

    /**
         * 颜色转换
         * @param h
         */
        private void flipColors(Node h){
            h.color = RED;
            h.left.color = BLACK;
            h.right.color = BLACK;
        }

红黑色的插入所有情况上面已经介绍了，总体是将红链接在树中向上传递。

在沿着插入点到根节点的路径向上移动时在所经过的每个结点中操作顺序如下:

    /**
         * 添加结点，如果存在修改，如果不存在创建新节点
         * @param h
         * @param key
         * @param val
         * @return
         */
        private Node put(Node h, Key key, Value val){
            if(h == null)//和父节点用红链接相连
                return new Node(key, val, 1, RED);
            int cmp = key.compareTo(h.key);
            if(cmp < 0) h.left = put(h.left, key, val);
            else if(cmp >0) h.right = put(h.right, key, val);
            else h.val = val;
            if(isRed(h.right) && !isRed(h.left)) h = rotateLeft(h);//右节点为红色，左节点为黑色
            if(isRed(h.left) && isRed(h.left.left)) h= rotateRight(h);//左节点是红色，且它的左子节点也为红色
            if(isRed(h.left) && isRed(h.right)) flipColors(h);//左右子节点均为红色
            h.N = size(h.left) + size(h.right) + 1;//修改节点个数
            return h;
        }

注意:根结点只能是黑色，每当根结点由红色变为黑色时黑链接高度就变为1。

测试:

    public class Test {
        public static void main(String[] args) {
            RBTree<Integer,Character> rbTree = new RBTree();
            rbTree.put(18,'A');
            rbTree.put(14, 'B');
            rbTree.put(22, 'C');
            rbTree.put(10, 'D');
            rbTree.put(15, 'E');
            rbTree.put(19, 'F');
            rbTree.put(25, 'G');
            rbTree.put(8, 'H');
            rbTree.put(11, 'I');
            rbTree.put(23, 'J');
            rbTree.put(7, 'K');
           rbTree.printfBST();
        }
    }

输出结果:

7 8 10 11 14 15 18 19 22 23 25 

删除操作比较复杂这里就不进行介绍了。
可以查看这篇博客
https://riteme.github.io/blog/2016-3-12/2-3-tree-and-red-black-tree.html