@Holmesee
2020-10-28T09:01:53.000000Z
字数 3846
阅读 988
树论
讲稿
by
- 题目描述一律放在引用里,简单的例题可能无标题无且solution也放在引用里。例子:
(题目描述)这是一道简单的例题
sol:!@#¥%%……- 题目太简单不要D我,太难也不要D我。
- 稿子写得比较简单,大家要认真听。
- 推荐一个图论作图工具 Graph Editor
- 推荐一个编辑器 Typora
- 推荐一个数学作图工具 GeoGebra
1. 轻工业
1.1 XX序
- dfs序:仅在第一次访问 时加入 。
- 括号序: 在第一次访问 与结束访问 时加入 。
- 欧拉序: 在第一次访问 与每次回溯 时都加入 。
明显dfs序可以对应子树。
给定一棵n个节点的树,m次查询,每次查询需要求出某个节点深度为h的所有子节点。
1.2 维护权值和
维护权值和这个问题,有这么几种常见情况:
1. 单点修改子树询问
2. 子树修改单点询问
3. 子树修改子树询问
4. 链修改单点询问
5. 单点修改链询问
请大家自行思考怎么做
1.3 重链剖分
给定一棵带边权的树,要求支持两种操作:
1.修改某条边的权值
2.询问树中两点之间唯一路径上的最大边权。
sol:线段树维护最大值,完了。
当然,也有稍微复杂点的。
[SDOI2011]染色
给定一棵 个节点的无根树,共有 个操作,操作分为两种:
- 将节点 到节点 的路径上的所有点(包括 和 )都染成颜色 。
- 询问节点 到节点 的路径上的颜色段数量。
颜色段的定义是极长的连续相同颜色被认为是一段。例如
112221由三段组成:11、222、1。
先解决序列问题,线段树维护颜色段数、左端颜色、右端颜色,合并随便讨论下。然后轻重链切换时注意也要合并。
2 树的直径与重心
2.1 树的直径
结论1: 离任意一个点最远的点一定是直径的一端。
这就导出第一种求法,两遍bfs。
第二种求法是dp,维护子树内最长链与次长链。
结论2: 两棵树合并后,新树的直径端点一定从原树直径端点中产生。
很多树论题一眼不会,可以从直径入手思考。
[APIO2010]巡逻
有一棵树,我们可以在树上加上 条边,使从一号节点出发遍历每条边并最终回到一号节点经过的路径最短。
-
-
加入一条边会形成一个环,环上所有边都少走一次。直接连直径。 -
可以扩展 的结论,再找一个环。但是一条边最多少走一次,因此把第一次求出的直径边权赋为 再求一次直径即可。注意这次不能两遍bfs。
2.2 树的重心
为奇数只有一个重心, 为偶数可能两个重心。
甩一波结论:
- 删除重心后所得的所有子树,节点数不超过原树的1/2;
- 树中所有节点到重心的距离之和最小,如果有两个重心,那么他们距离之和相等;
- 两个树通过一条边合并,新的重心在原树两个重心的路径上;
- 树删除或添加一个叶子节点,重心最多只移动一条边。
[CSP2019]树的重心
给出一棵树,我们知道,断掉一条边后,它会分成两棵子树,定义这条边的贡献为这两棵子树的重心的编号和。求所有边的贡献和。
考虑每个点的贡献。
先用整棵树的重心作根。
除了 以外点 ,断掉 子树内的点显然不能使 成为重心。
设 为 的子树大小, 为 的重儿子的大小, 为断掉的边, 为 另一棵(不包括 那棵)子树的大小。
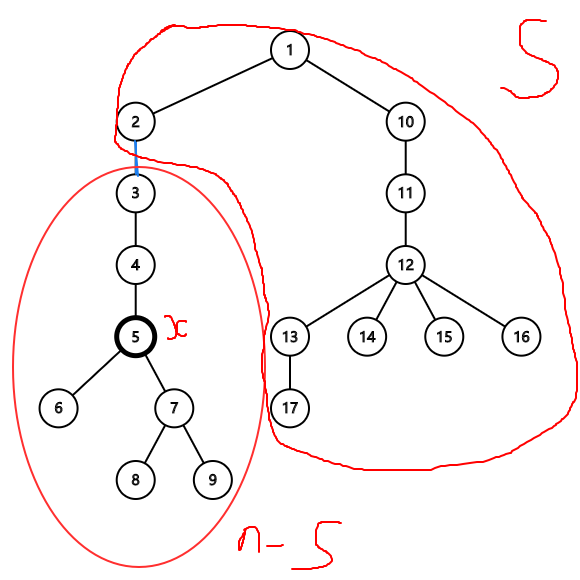
如图, 号点为 ,假设要断掉 。
那么要使 成为圆圈里面这棵子树的重心,要满足
- 在 的子树外。
先不管第一条,第二条和第三条合并为 。
这个大致做法是用树状数组动态维护每个满足条件2.3.的 的个数,询问就是区间查。
然后减掉在 子树内的合法边,这个可以用类似天天爱跑步的做法,考虑进 与出 的变化值。
还要算出 的贡献。
设 的儿子中子树最大的节点为 ,次大的节点为 。
若 在 中,则需满足 。
若 在 中,则需满足 。
可以顺便处理。
3 基环树
- @ 已经讲过了。
- 我会的是 @ 讲过的的子集。
- 所以我不用讲了。
4 小清新例题
4.1 [HDU5156]
节点树,根为 ,一个节点可能有多个不同颜色的苹果,但苹果总数为 。任务是:对于每个节点,输出它的子树内有多少种颜色的苹果。
思路1
对每种颜色分开考虑贡献。对每个颜色搞个虚树,要做到虚树上每个点只贡献一次。
思路2
转线性问题,假设要询问 中的颜色种数,求出 表示上一个与 颜色相同的位置,那么
扩展到树上相当于询问 个子树区间。这是个经典的二维数点问题,扫描线解决。
4.2 [NOIP2016]天天爱跑步
个节点的树,有 个玩家,第 个玩家会在时刻 出现在 然后以每秒一条边的速度沿唯一路径跑到 ,然后瞬间消失。每个节点上有一个观察员,他会在 时刻记录在 号节点停留的玩家个数 。求出 数组。
玩家们都可以拆成从下到上的路径,比如一种情况下, 对 有贡献当且仅当 开个全局桶统计。具体地说,看进 的子树,与出 的子树时桶的差值。注意 lca 处可能会算重,要减去。
4.3 [CF280C] Game on Tree
给定一棵有根树,每次随机选一个未被删除的点,将以它为根的子树删除。
求删除整棵树所用的期望步数。
期望的线性性。
你可以理解成,总的期望等于每个点贡献期望的和。
一个点有贡献,即被作为根删除的概率是多少呢?。
所以说遇到期望题优先考虑一下期望的线性性,就像遇到位运算题优先按位考虑。
4.4 ???
给你一棵树,问距离为 的倍数的无序点对有多少个。
如果淀粉质学傻了可能直接上点分了,但这题不需要。
表示以 为根的子树中到 距离 mod 3等于 的点的个数。
合并点 的儿子时,顺便统计当前儿子与前缀儿子组成的贡献。
4.5 [JZOJ5050]颜色树
个点的树,每个点有一种颜色。一共有 种颜色。求含 种颜色的路径数量。
Ps:出题人特意卡了空间 禁用状压 DP
状压咋做?。FWT优化到 。这咋过???
[JZOJ5050]颜色树 咋状压?
在座的能教教我吗。
正解大概是 的容斥做法。枚举不选颜色集合 ,删掉这些点,然后剩下一坨联通块,求出两端在不同联通块的路径数量。
4.6 [HDU4912]
个节点的树,给出 条路径 ,你需要选出尽量多的路径,要求路径之间没有公共点。
贪心,考虑从下往上贪心地选取
自底向上,对于lca在 上的一条路径,如果可选,那么一定会选。
怎么判断是否可选?
若选取了lca为 的一条路径,将整棵子树 均标记,注意若发现一个点已标记即可返回。
4.7 [bzoj1117]救火站
给你一棵 节点的树,现在要建立一些消防站,有以下要求:
1.消防站要建立在节点上,每个节点可能建立不只一个消防站。
2. 每个节点应该被一个消防站管理,这个消防站不一定建立在该节点上。
3. 每个消防站可以管理至多 个节点。
4. 消防站只能管理距离(两点间最短路径的边数)不超过 的结点。请问至少要设立多少个消防站。
我们的策略是,到万不得已时才放消防站。
设 表示 的第 层还有多少节点需要管理, 表示 的第 层还余下多少控制力。
void dfs(int x,int f){fa[x]=f; need[x][0]=1;for(int i=head[x];i;i=e[i].next){int to=e[i].to;if(to==fa[x]) continue;dfs(to,x);for(int j=1;j<=k;j++) need[x][j]+=need[to][j-1];for(int j=k-1;j>=0;j--) lef[x][j]+=lef[to][j+1];}ll tmp=(need[x][k]+s-1)/s;ans+=tmp;lef[x][k]+=(ll)tmp*s;for(int i=0;i<=k;i++){if(lef[x][i]){for(int j=i;j>=0&&(j>=i-1||x==1);j--){if(lef[x][i]<=need[x][j]){need[x][j]-=lef[x][i];lef[x][i]=0;break;}lef[x][i]-=need[x][j];need[x][j]=0;}}}}int main(){……dfs(1,0);for(int i=0;i<=k;i++) tot+=need[1][i];ans+=(tot+s-1)/s;……}
4.8 [CF735E]Ostap and Tree
问对一棵树染色,初始无色,要求距每个点最近的染色点的距离不超过 的染色方法总和 。