数论函数

未分类

---

记号

$\epsilon(n)=[n=1]$
$I(n)=1$
$d(n)=\sum\limits_{d|n}I$
$\sigma(n)=\sum\limits_{d|n}d$
$id(n)=n$
$\mu(n)=\begin{cases} (-1)^w &\ n=\prod\limits_{i=1}^{w}p_i&\\0 &\ n=p^2\prod\limits_{i=1}^{w}p_i^{c_i}&\end{cases}$
$\varphi(n)=\sum\limits_{i=1}^{n}[i\perp n]$

卷积

定理1：积性函数的卷积仍为积性函数
公式1：$\mu*I=\epsilon$
公式2：$\varphi*I=id$

补充公式

1. $$\sum_i^ni[i\perp n]=n\varphi(n)/2$$
2. (1.推论） $$\sum_i^n\sum_j^nij[i\perp j]=\sum_i^ni^2\varphi(i)$$
3. $$d(nm)=\sum_{i|n}\sum_{j|m}[i\perp j]$$

杜教筛

原理

设 $S(n)=\sum_{i=1}^{n}f_i$
则 $S(n)g(1)=\sum_{i=1}^{n}(f*g)(i)-\sum_{i=2}^{n}g(i)S(\lfloor n/i \rfloor)$
线性筛预处理 $S$ 的前 $n^{2/3}$ 项，整除分块并记忆化可以做到 $\Theta(n^{2/3})$ 复杂度。

例子

1.求 $\mu$ 前缀和

利用 $\mu*I=\epsilon$。

2.求 $\phi$ 前缀和

利用 $\varphi*I=id$。
也可以算 $\sum_i\sum_j[gcd(i,j)=1]=\sum_i\mu(i) {\lfloor n/i \rfloor}^2$ ，然后减一再除以二。

3.求 $f=F*I$ 前缀和，其中 $F(n)=\mu(n)*n$

$F$ 里面乘了个 $id$，所以卷一个 $id$ 把它消掉。
构造 $(F*id)(n)\\=\sum_{d|n}F(d)n/d\\=\sum_{d|n}\mu(d)·d·n/d\\=n\sum_{d|n}\mu(d)\\=[n=1]$
则 $F*id=\epsilon$
那么 $F*\varphi*I=\epsilon \Rightarrow f*\varphi=\epsilon$
就可以愉快地杜教筛了。
可能还得筛 $\varphi$ 的前缀和

4.「LuoguP3768」简单的数学题

求 $\left(\sum_{i=1}^n\sum_{j=1}^n ij \gcd(i,j)\right) \bmod p$

首先用欧拉反演把式子化成
$\sum_k\varphi(k)·k^2·F(n/k),F(n)=\sum_i^ni^3$
然后杜教筛 $\varphi(k)·k^2$ 的前缀和。构造就卷上 $id^2$。

有意思的题

「LuoguP6222」简单题加强版

求

$$\sum_i^n\sum_j^n(i+j)^k(i,j)\mu^2((i,j))\bmod 2^{32}$$
$k$ 是常量，多组询问。

写一下主要步骤：

$$Ans=\sum_d^nd\mu^2(d)\sum_i^{n/d}\sum_j^{n/d}[i\perp j](id+jd)^k$$
$$=\sum_d^nd\mu^2(d)\sum_t^{n/d}\mu(t)\sum_i^{n/dt}\sum_j^{n/dt}(idt+jdt)^k$$
枚举 $T=dt$
$$=\sum_T^nT^k\sum_i^{n/T}\sum_j^{n/T}(i+j)^k\sum_{d|T}d\mu^2(d)\mu(T/d)$$
令 $g(n)=\sum_i^n\sum_j^n(i+j)^k$，$f(n)=\sum_{d|n}d\mu^2(d)\mu(n/d)$。
先来解决 $g(n)$，
$$g(n)=\sum_{i=2}^{2n}i^k\sum_{j=1}^n[1\le i-j \le n]$$
$$=\sum_{j=1}^n\sum_{i=2}^{2n}i^k[j+1\le i \le n+j]$$
令 $s(n)=\sum_i^n i^k$，则
$$g(n)=\sum_{j=1}^n(s(n+j)-s(j))$$
接下来只需要处理 $s_n$ 的前缀和。

如何线性筛 $f(n)=\sum_{d|n}d\mu^2(d)\mu(n/d)$？
假设现在枚举的质因子为 $p$，要求出 $f(ip)$。根据积性函数的性质，设 $ip$ 中因子 $p$ 的次数为 $d$，则 $f(ip)=f(i)f(p^d)$。分类讨论 $d$ 的取值，能快速求出 $f(p^d)$ 就行了。
1. $f(p)=\mu(p)+p=p-1$；
2. $f(p^2)=1\mu^2(1)\mu(p^2)+p\mu^2(p)\mu(p)+p^2\mu^2(p^2)\mu(1)=-p$；
3. $d>2$ 的情况 $f(p^d)=0$。

「CF1139D」Steps to One

序列初始为空，每次随机从 $[1,m]$ 中选一个数加到序列末尾，当序列中所有数的 $gcd$ 等于 $1$ 时停止，求期望长度。
$m\le 10^5$

本来这是个可以推出 $\Theta(m)$ 甚至 $\Theta(\sqrt m)$ （用数论分块）的数学题，结果因为数据范围比较小被我直接用 $\Theta(m\log m\sqrt m)$ 的DP过了……
偷一张题解的图：

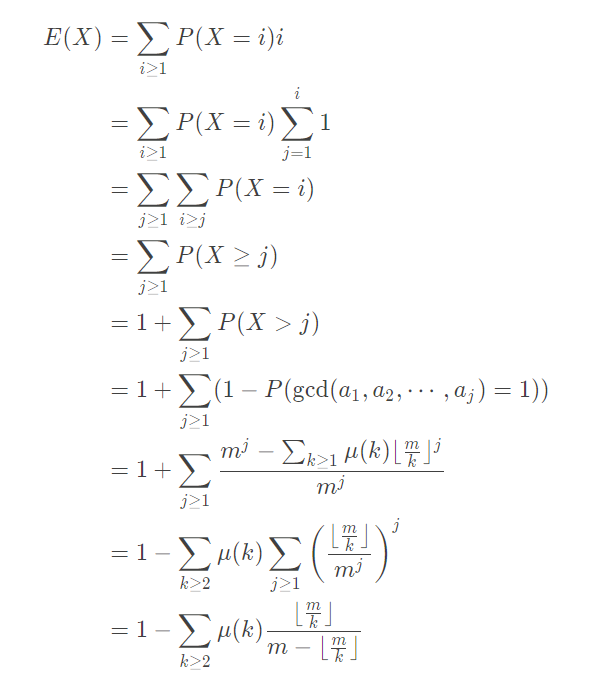
奇妙之处在于第一步恰好转至少，还有钦定前 $i$ 个不互质。