反悔贪心

未分类

有人把这个东西分成两种：贪心自动机和贪心堆。在此主要介绍前者。

例子

树上k条路径最大权值和

边有边权，树上选择k个边不相交的路径，总和最大（权值有正有负）

求k次树的直径，每次把直径上的边权取反即可。

CF865D Buy Low Sell High

已知接下来 $n$ 天的股票价格，每天可以买入当天的股票，卖出已有的股票，或者什么都不做，求 $n$ 天之后最大的利润。

显然答案是由若干对卖出价-买入价组成的。维护一个小根堆。对于 $a_i$，先放进堆里作可能的买入价，如果$a_i$比 $top$ 大，则 $ans+=a_i-top$ 并 $pop$ 掉 $top$ ，但是 $a_i$ 作为卖出价可能不是最优的，所以我们把再放一个 $a_i$ 进堆，这样即使以后可能有比 $a_i$ 更大的卖出价也能反悔。

BZOJ2151 种树

有 $n$ 个位置，每个位置有一个价值。有 $m$ 个树苗，将这些树苗种在这些位置上，相邻位置不能都种。求可以得到的最大值或无解信息。

维护一个大根堆，每次选最大元素 $C$，把它删了后放个 $A+B-C$ ($A$ 和 $B$ 是 $C$ 的相邻元素）进堆就行了。

楼房搭建

有一个非负序列 $a_{i}$，每次可以进行两种操作：
1. $a_i-=1,a_{i+1}-=2$
2. $a_i-=2,a_{i+1}-=1$
求使得所有元素小于等于 $0$ 的最小操作次数。

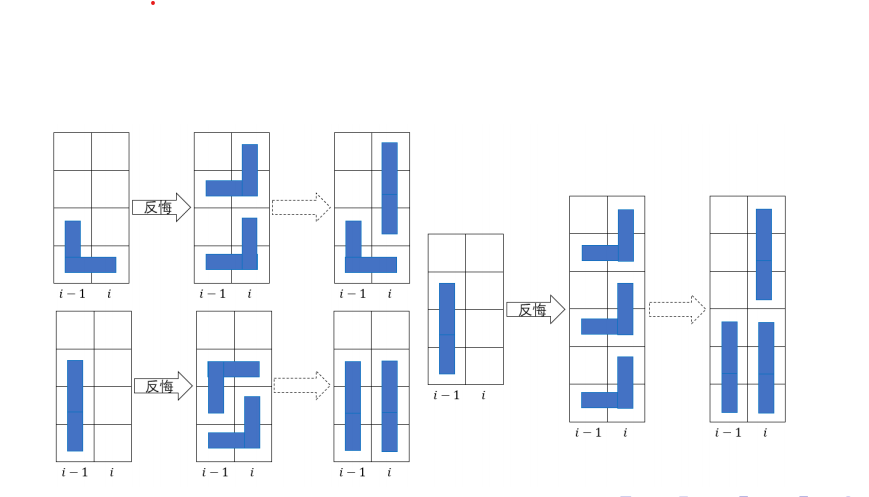
我们朴素的贪心策略当然是对 $a_i$ 尽可能多地使用 $2$ 操作，考虑反悔 $2$ 操作，就是上图中的第一个反悔，相当于添加了一个新的操作叫 $3$ 操作，可以使 $a_i-=2$，但是 $3$ 操作也需要反悔，于是有了另外的两种反悔。
Code

for(int i = 0; i < n; i++)
{
    h[i] = max(h[i], 0ll);
    t1 = min(h[i] / 3, a[i]);
    h[i] -= t1 * 3;
    t2 = h[i] / 2;
    h[i] -= t2 * 2;
    t3 = h[i];
    h[i] -= t3;
    h[i+1] -= t2 + t3 * 2;
    a[i+1] = t1 * 2 + t2;
    ans += t1 + t2 + t3;
}

共性

1. 问题是一个线性的决策过程，每次决策要付出一个代价，总代价是一定的。
2. 每次采取朴素贪心策略（即局部最优），但是要把撤销操作加入可选决策集。
3. 撤销操作应该满足：能够完全填补被撤销操作，且代价要比被撤销操作大（当然，往往恰好大 $1$）。