吴恩达机器学习002线性回归&&梯度下降

算法 机器学习

模型描述

先再回顾一下监督学习算法预测房价的例子

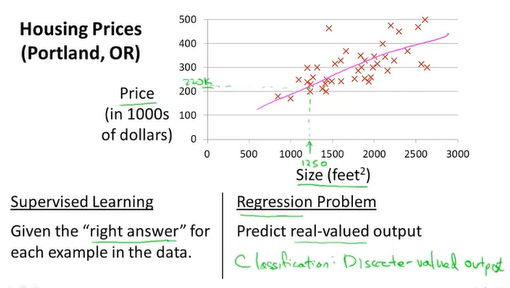
 下面给定一些符号来描述训练集

m表示训练样本的数目，x表示输入的参数，y表示输出的参数，（x，y）表示一组训练样本，（x⁽ⁱ⁾，y⁽ⁱ⁾）则用来表示特定的训练样本。

线性回归算法（单变量线性回归）

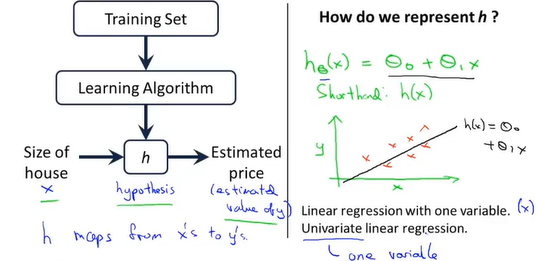
训练集通过学习算法来得到一个假设函数h，通过这个假设函数h我们可以通过输入房子的占地面积来得到房子的售价，从而拟合出一条一次直线，这个算法又叫线性回归算法

代价函数（平方误差函数）

接下来讨论如何确定参数（parameter）θ₀和θ₁

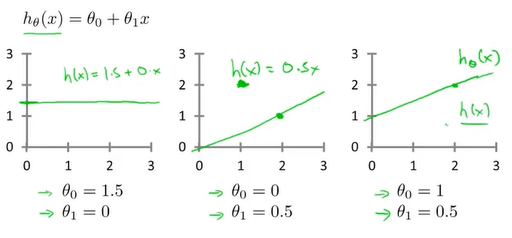
代价函数:J(θ₀,θ₁)=1/2m*∑^m_i=1(h_θ(x⁽ⁱ⁾)-y⁽ⁱ⁾)  

代价函数（一）

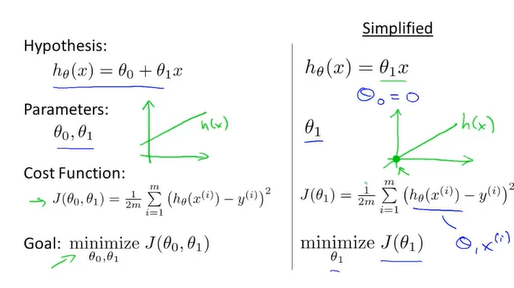
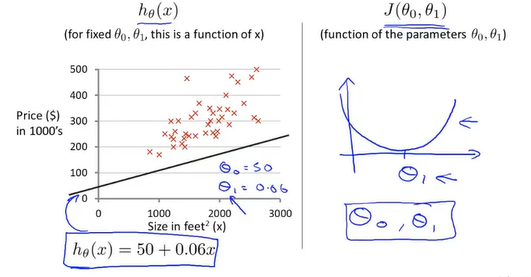
现在先让θ₀取0 ，那么假设函数就是一条经过原点的直线，代价函数的形式则就是为了求J(θ₁)的最小值

从图中可以得知，当θ取不同的值时，假设函数对应着不同的直线，代价函数则取到不同的值，当θ=1时代价函数取值为0，表示拟合的程度最好。

代价函数（二）

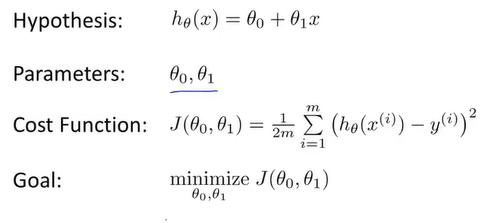
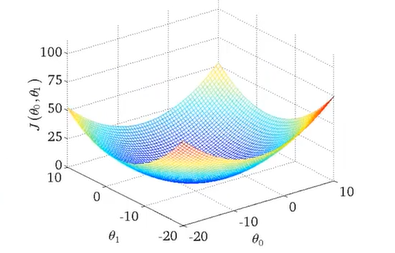
这一次保留假设函数里所有参数，按照同样的分析方法可得 一个三维碗装的代价函数

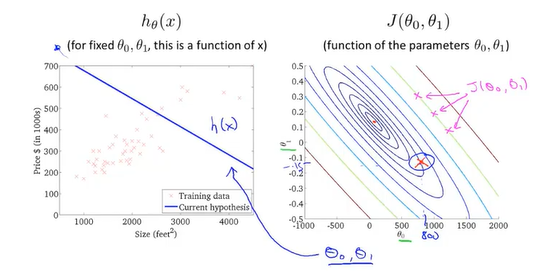
为了能够更加方便地在平面图上表示代价函数，我们采用等高线来表示代价函数

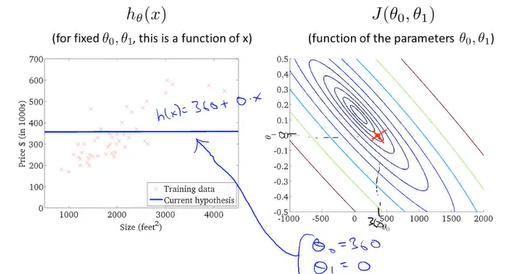
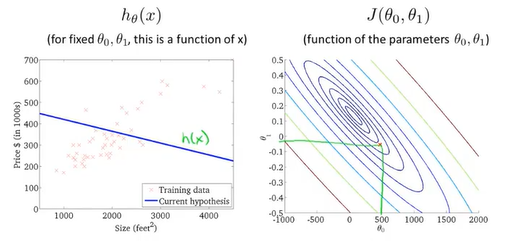
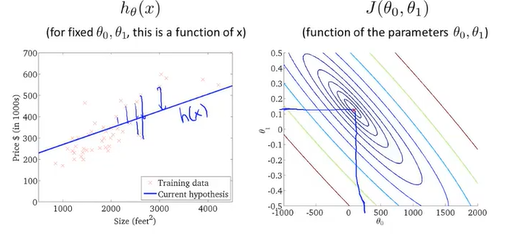
梯度下降算法

我们选择从0开始改变参数直到我们得到代价函数地最小值

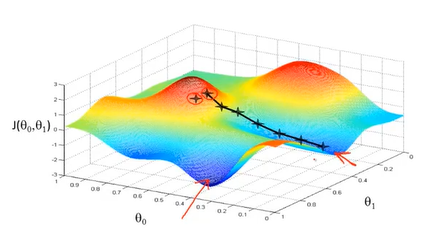
假设图中的最高的黑点时你在所在地位置，把图中的模型想象作一座山，你在黑点环顾周围要找到最快地下山路线，于是你走了一步到了下一个黑点，这是你再反复重复上一步操作你就能走到一个局部最低地地方（局部最优解）。

图中为梯度下降算法地数学原理，α代表的是学习率，学习率越大，下山地速度越快（梯度下降越快），反之越慢。

θ₀和θ₁一般腰同时更新，所以在计算时先用temp值保存，再同时更新，平时人们所说地梯度下降指的是同时更新地梯度下降 。

（计算机里 := 代表地是赋值 普通的等号表示的是判断）

下面讲讲述变化率和微分，先用单变量地形式来讨论

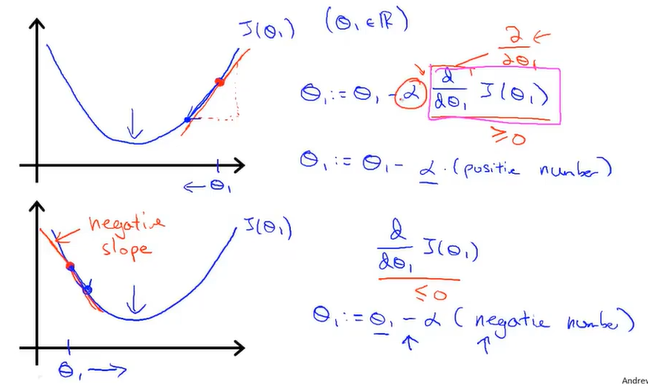
从右边来看，做梯度下降算法会让θ₁减小从而趋紧代价函数最小值所对应的值，相反的从左边取值的话会向右趋紧最小值

下面讨论学习率α对代价函数的影响

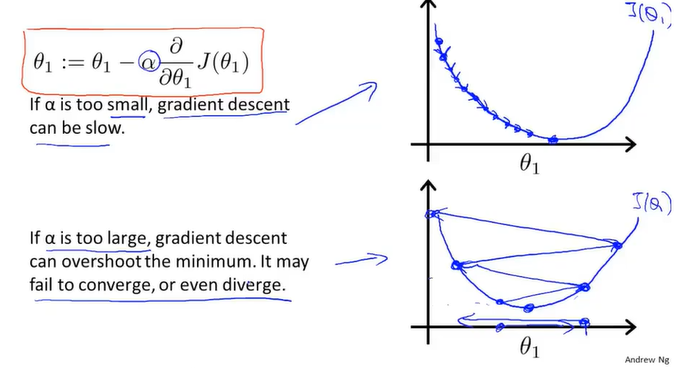
当学习率过小时，梯度下降的速度将会很慢，因为每次都只走一小步；但是要是学习率过大，有可能会直接越过了最低点到达另一侧，再次返回走得可能越来越大导致无法收敛。

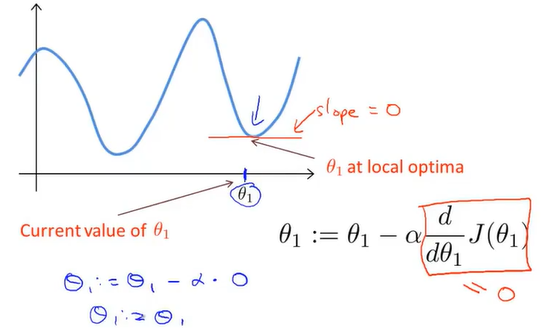
假设已经到达的局部最优解，那此地的偏导数为0，更新变得没有用处了，所以会一直保持不变

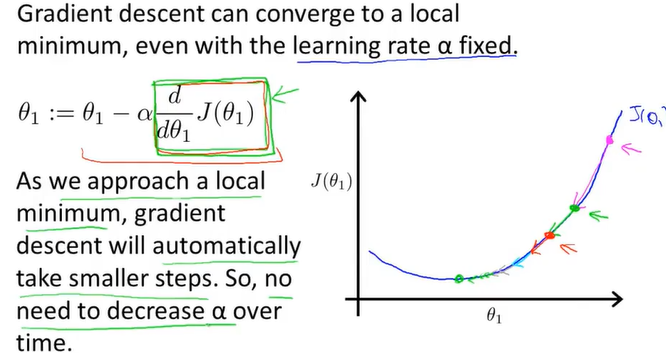
当梯度下降时，斜率会减小，所以不需要手动减小学习率

线性回归的梯度下降（Batch梯度下降）

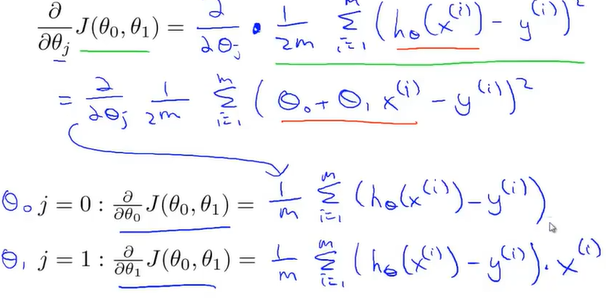
现在对代价函数求偏导，得到的值再代会梯度下降方程，得到如下方程

挑选一个初始值作为开始梯度下降的起点

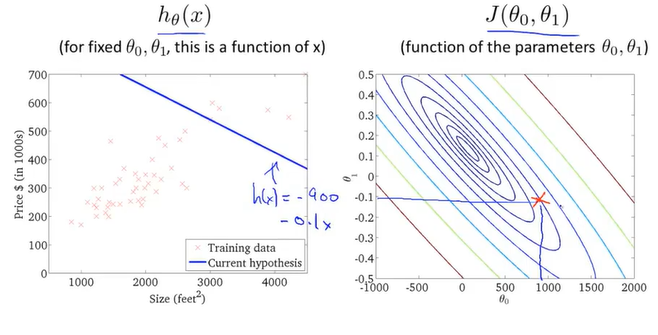
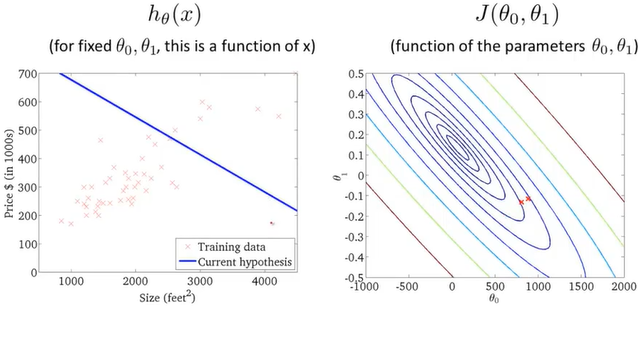
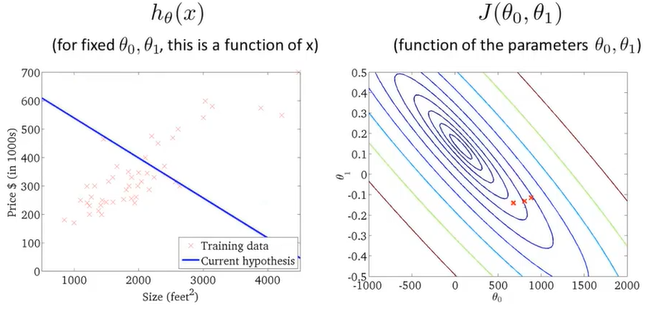
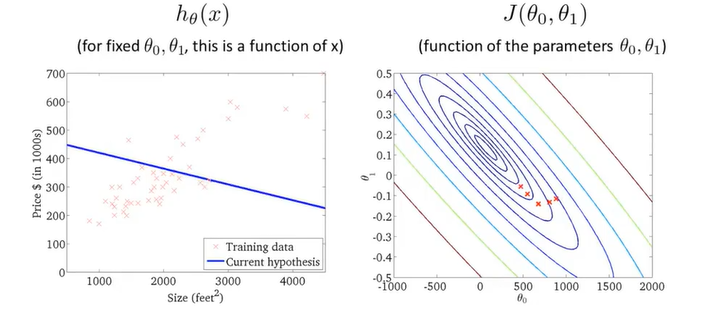
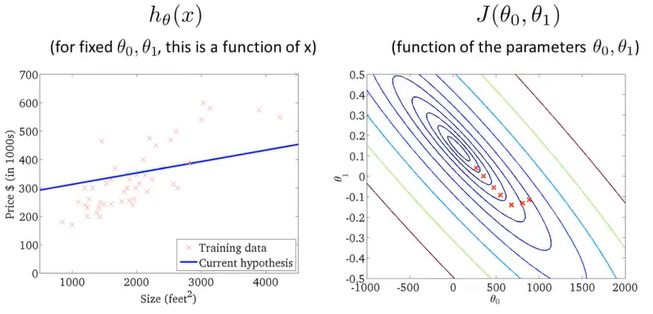
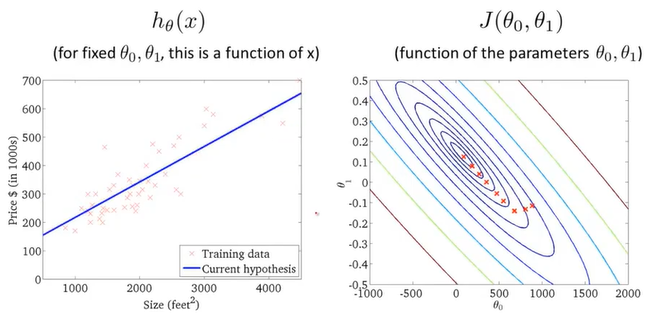
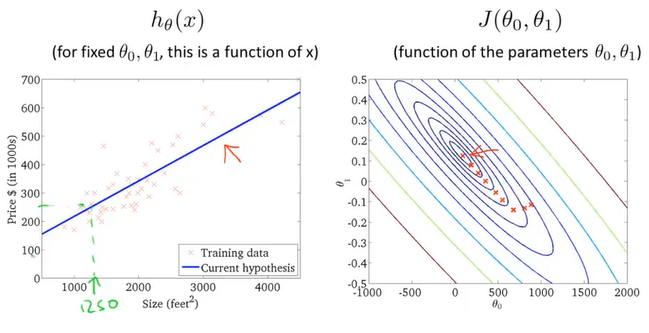
通过不断地拟合，得到了一条房价和房屋大小的关系图