吴恩达机器学习004多元梯度下降

算法 机器学习

特征和多项式回归

正规方程

多功能

我们引入更加多的特征来对房价进行进一步评估，同时也新增一些符号来帮助表示参数。

n用来表示特征（feature）量，x⁽ⁱ⁾这是表示的就不是一个值了，而是一组向量 ，同时用x_j⁽ⁱ⁾来表示向量里的具体哪一个参数 

有了多个特征之后假设函数就应该将所有特征考虑进去才合适，于是就有了新的形式

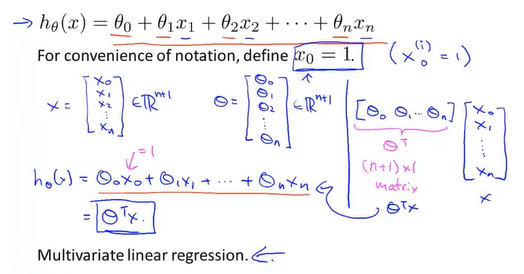
上一章讲了矩阵和向量，这个时候可以学以致用了，假设函数可以写成如上形式，至于为什么θ^T为什么要放左边，因为行向量只能放左边，列向量只能放右边，不然不能相乘 

多元梯度下降法

类似的，我们也可以列出相应的代价函数

特征缩放

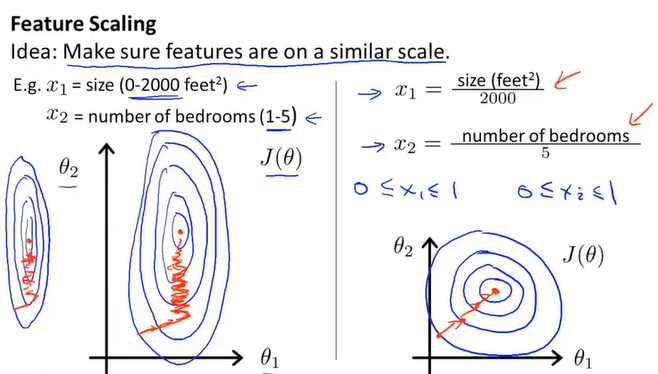
当两个特征的取值范围相差过大时，会出现如左边图一样的细长椭圆形，这样的话梯度下降会收敛地很慢，但如果在之前我们将特征进行缩放的话，可以加快梯度下降地速度，减少迭代地次数。

特征缩放到地范围接近【-1，1】即可，但最好不要像后两个例子一样

还可以用均值归一化来加快收敛，如图，将参数减去特征的平均值再除以特征地范围（最大值-最小值  或者  标准差）

学习率α

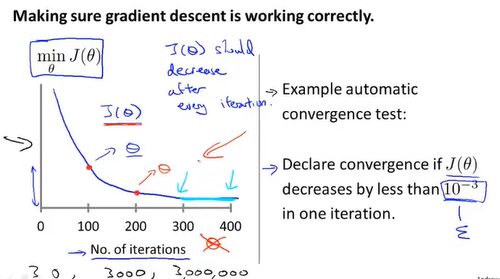
为了知道代价函数是否收敛，我们可以每隔规定迭代次数进行采样绘图，当图像地线趋于平缓时代表函数收敛，从而判断梯度下降是否在正常工作

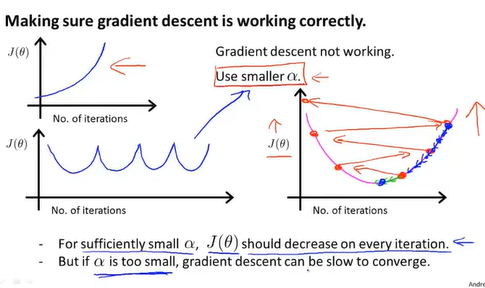
当图像呈现出以上左图两种情形时，可能是因为学习率过大了，这式可以换一个小一点地学习率。数学家已经证明只要学习率足够小，函数会一直下降，迭代次数会很多，收敛速度会很慢

在寻找合适学习率时可以尝试按10的倍数来找，找到合适的再在中间按3的倍数找，直到找到合适的学习率

特征和多项式回归

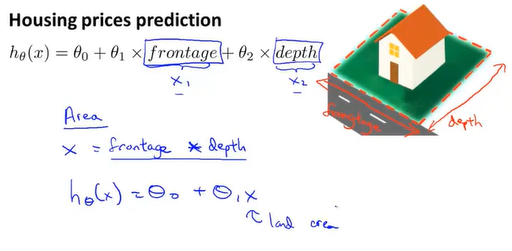
在对问题进行分析时，可以现有的特征组合出新的更加易于我们分析的特征，比如将房子的长和宽相乘，得到面积特征和价格进行比较

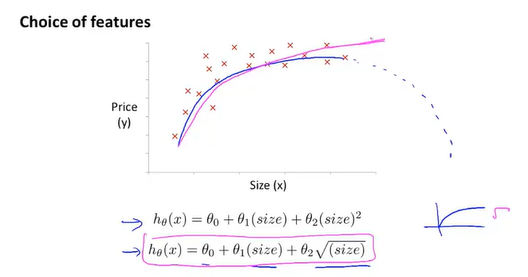
多元线性回归如上图，当我们发现直线不能很好的拟合时，我们可以用抛物线来拟合，但抛物线会下降，所以可以用三次曲线来拟合得到一条良好的关系图，这时样本就可以是平方或立方，这时特征缩放显得尤为重要，适当的缩放能把值得范围变得又可比性

正规方程

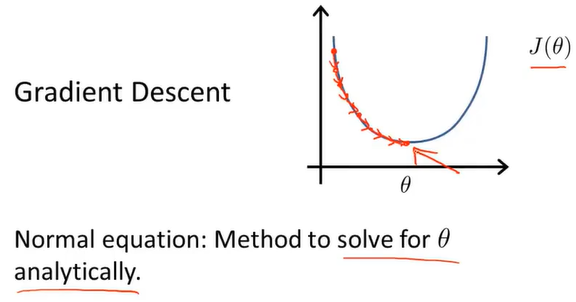
正规方程和梯度下降算法不同之处在于，梯度下降算法是J(θ)得最小值，而正规方程则是求θ，所以正规方程可以一步到最优解，但正规方程有好处有坏处，

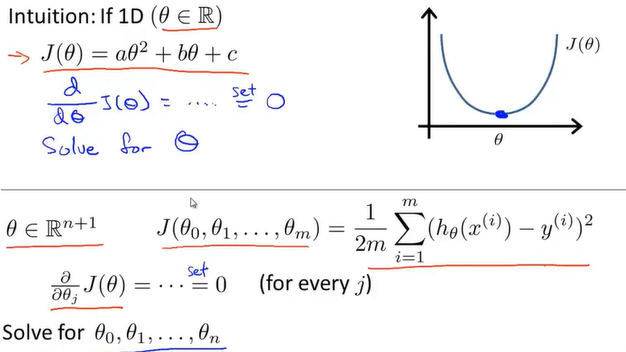
为了求得最小值时的θ，可以对代价函数求偏导，然后全部置零解出每一个θ

如图有四个训练样本，加上一列后写成矩阵得形式，再根据左下角公式可以算出θ得值

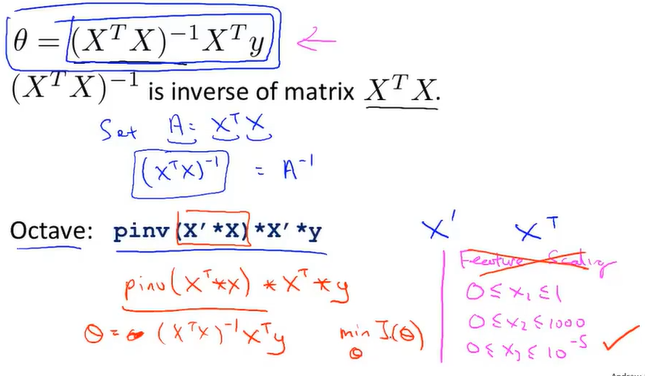
当使用正规方程时，特征缩放便不那么重要了

梯度下降和正规方程得优缺点比较

正规方程再矩阵不可逆得情况下得解决方法

在octave里面求解逆有两种函数pinv和inv，pinv在逆不存在时也能给出θ得正确解

通常出现不可逆得情况有如上情况，特征始终满足乘积为定值，或者当训练集少于特征量时