HMM、CRF模型

机器学习&深度学习

---

首发时间：2020.10.8
作者：zakexu（个人主页）

---

目录

---

一、HMM模型

（一）简介

1、隐马尔科夫模型（Hidden Markov Model，HMM）：关于时序的概率模型，描述由一个隐藏的马尔科夫链随机生成不可观测的状态序列，再由各个状态随机生成观测序列的过程。
（1）状态序列：HMM生成的状态的序列，称为状态序列。
（2）观测序列：每个状态生成一个观测，而由此产生的观测的随机序列，称为观测序列。
（3）序列的每一个位置又可以看作是一个时刻。
2、HMM模型的2个基本假设：
（1）齐次马尔科夫性假设：假设隐藏的马尔科夫链在任意时刻 t 的状态只依赖于其前一时刻的状态，与其他时刻的状态及观测无关，也与时刻 t 无关。
（2）观测独立性假设：假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态，与其他观测及状态无关。
3、HMM模型可以表示为：

$$\lambda=(\pi,A,B)$$

其中$\pi$表示状态的初始概率，$A$表示状态的转移概率矩阵，$B$表示状态产生预测值的观测概率矩阵。
假设状态取值$S$、观测取值$V$、状态序列$I$、观测序列$O$可以表示如下：

$$S=(s_1,s_2,...,s_N) \\V=(v_1,v_2,...,v_M) \\I=(i_1,i_2,...,i_T) \\O=(o_1,o_2,...,o_T)$$

（1）状态的初始概率$\pi$

$$\pi=[\pi_i]_{1*N} \\\pi_i=p(s_i)$$

（2）状态的转移概率矩阵$A$

$$A=[a_{ij}]_{N*N} \\a_{ij}=p(i_{t+1}=s_j|i_{t}=s_i)$$

（3）状态产生预测值的观测概率矩阵$B$

$$B=[b_{jk}]_{N*M} \\b_{jk}=p(o_{t}=v_k|i_{t}=s_j)$$

4、HMM模型的3个基本问题：
（1）学习问题：给定观测序列，估计HMM模型参数。
（2）概率计算问题：给定HMM模型下，求观测序列的概率。
（3）预测问题：给定HMM模型跟观测序列，求状态序列。

（二）学习问题

1、假设有训练数据$\{(i_1,o_1),(i_2,o_2),...,(i_L,o_L)\}$，那么可以用极大似然估计的方法来得到模型参数$\lambda$。
2、状态的初始概率$\pi$可学习如下：

$$\pi_i=\frac{sum(i_t=s_i)}{L}$$

3、状态的转移概率矩阵$A$可学习如下：

$$a_{ij}=\frac{sum(i_t=s_i,i_{t+1}=s_j)}{sum(i_t=s_i)}$$

4、状态产生预测值的观测概率矩阵$B$可学习如下：

$$b_{jk}=\frac{sum(i_t=s_j,o_t=v_k)}{sum(i_t=s_j)}$$

（三）概率计算问题

1、假设$t$时刻状态为$i_t$，观测序列为$(o_1,o_2,...,o_t)$，那么可以有前向概率表示如下：

$$\alpha_{ts_i}=p(o_1,o_2,...,o_t;i_t=s_i|\lambda)$$

2、初始化前向概率如下：

$$\alpha_{1s_i}=\pi_ib_{s_io_1}$$

3、递归计算如下：

$$\alpha_{(t+1)s_i}=[\sum_j\alpha_{ts_j}a_{s_js_i}]b_{s_io_{t+1}}$$

4、最终概率累加可得：

$$p(O|\lambda)=\sum_i\alpha_{Ts_i}$$

（四）预测问题

1、解决预测问题用的是维特比算法：

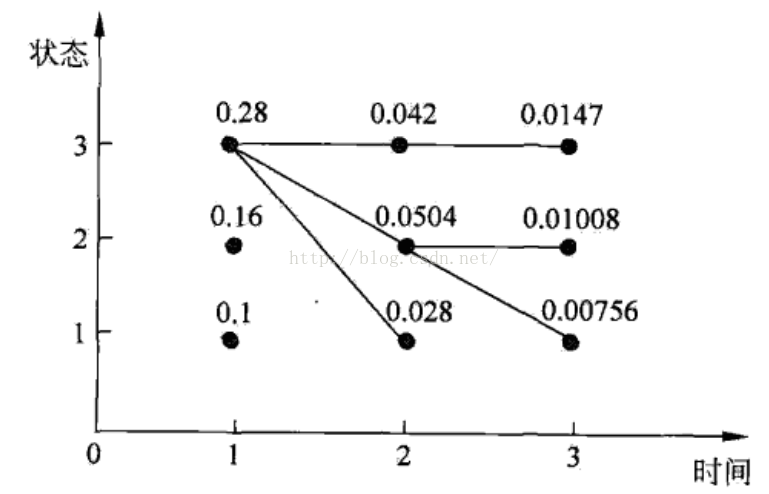
（1）每一列代表一个时刻$t$。
（2）初始化时，第一列$t_1$可根据$o_1$得到每个状态的概率分布，同时记录概率最大的状态。
（3）当往后迭代时，根据$o_t$可以得到当前时刻的状态分布，对于每一个状态，结合以往的状态路径以及状态转移矩阵，记录当前时刻每个状态的之前概率最大状态路径的最后一个节点。
（4）迭代到最后一个时刻$T$，根据每个状态记录的之前最大概率状态路径的最后一个状态节点往前回溯，即可得到最佳状态路径，比如上图，最佳路径就是3-3-3。

二、CRF模型

（一）简介

1、条件随机场（Conditional Random Field，CRF）是给定一组输入随机变量条件下另一组输出随机变量的条件概率分布模型，其特点是假设输出随机变量构成马尔可夫随机场。条件随机场常用于序列标注问题，比如命名实体识别等。

（二）马尔可夫随机场

1、马尔可夫随机场又称为概率无向图模型，假设有联合概率分布$P(Y)$，由无向图$G=( V , E )$表示（节点表示随机变量，边表示变量之间的依赖关系），在图$G$中，如果联合概率分布$P(Y)$满足成对、局部或全局马尔可夫性，则称此联合概率分布为概率无向图模型。

（1）成对马尔可夫性

$$P(Y_u,Y_v|Y_O)=P(Y_u|Y_O)P(Y_v|Y_O)$$

其中$u,v$是属于图中任意两个没有边连接的节点，$O$表示其余的节点。

（2）局部马尔可夫性

$$P(Y_u,Y_O|Y_V)=P(Y_u|Y_V)P(Y_O|Y_V)$$

其中$u$是属于图中任意的节点，$V$表示跟$u$连接的节点，$O$表示其余的节点。

（3）全局马尔可夫性

$$P(Y_U,Y_V|Y_O)=P(Y_U|Y_O)P(Y_V|Y_O)$$

设结点集合$U,V$是在无向图$G$中被结点集合$O$分开的任意结点集合。

2、概率无向图模型中联合概率分布可以表示如下：

$$P(Y)=\frac{1}{Z}\prod_{C}\Psi_C(Y_C) \\Z=\sum_Y\prod_{C}\Psi_C(Y_C)$$
其中，$C$是无向图的最大团，无向图$G$中任何两个节点均有边连接的节点子集称为团，若$C$是无向图$G$的一个团，并且不能再加进任何一个$G$的节点使其成为一个更大的团，则称此$C$为最大团。$Y_C$是$C$的节点对应的随机变量，$\Psi_C(Y_C)$是$C$上定义的严格正函数，一般为指数函数。

（三）条件随机场

1、设$x$与$y$是随机变量，$P(y|x)$是在给定$x$的条件下$y$的条件概率分布。若随机变量$y$构成一个由无向图$G = ( V , E )$表示的马尔可夫随机场，则称条件概率分布$P(y|x)$为条件随机场。
2、在现实情况下，我们一般假设$x$与$y$具有相同的图结构，并且考虑线性链的情况：

$$P(y_t|x;y_1,y_2,..,y_T)=P(y_t|x;y_{t-1},y_{t+1})$$
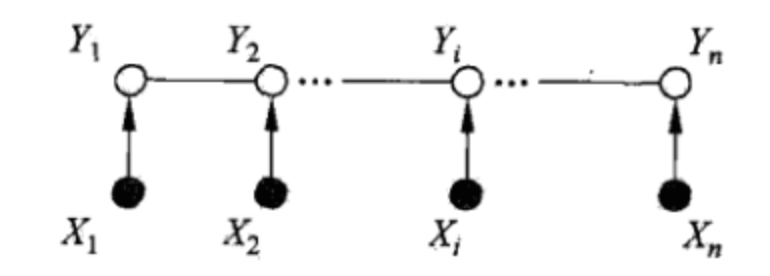
此时最大团为相邻两个节点的集合。在标注问题中，$x$表示输入观测序列，$y$表示对应的输出标记序列或状态序列。
3、条件随机场的概率分布可以表示如下：
$$P(y|x)=\frac{1}{Z(x)}exp(\sum_{i,k_1}\lambda_{k_1}t_{k_1}(i,x,y_{i-1},y_i)+\sum_{i,k_2}\mu_{k_2}s_{k_2}(i,x,y_i)) \\Z(x)=\sum_yexp(\sum_{i,k_1}\lambda_{k_1}t_{k_1}(i,x,y_{i-1},y_i)+\sum_{i,k_2}\mu_{k_2}s_{k_2}(i,x,y_i))$$

其中$t_{k_1}$表示转移（transfer）特征函数，$s_{k_2}$表示状态（state）/发射特征函数，$\lambda_{k_1}$跟$\mu_{k_2}$则表示对应的权重。
由上可以看出，在一个条件随机场中，是可以定义多个转移特征函数以及多个状态特征函数的。当转移特征函数用状态转移概率矩阵表示，状态特征函数用观测概率矩阵表示，则条件随机场可以等同于hmm模型。
4、crf跟hmm模型同样有3个基本问题：学习、概率计算、预测，解决方案跟hmm类似。

三、HMM VS CRF

1、HMM是生成模型，CRF是判别模型。
2、HMM是有向图，CRF是无向图。