LR、Softmax、FM、FFM模型

机器学习&深度学习

---

首发时间：2020.6.26
作者：zakexu（个人主页）

---

目录

---

一、LR模型

（一）简介

1、定义：逻辑回归（Logistic Regression，LR）模型属于二分类模型，其假设数据服从伯努利分布，通过极大化似然函数的策略，运用梯度下降算法来求解参数，从而达到将数据二分类的目的。

注：伯努利分布指的是对于随机变量$X$，分别以概率$p$跟$1-p$取$1$和$0$为值。

（二）模型

1、根据LR模型的定义，其模型（默认用$+1$跟$0$表示正负样本）可以表示为：

$$p(y|x;\theta)=h_\theta(x)^{y}(1-h_\theta(x))^{(1-y)}$$

$h_\theta(x)$，也就是伯努利分布中的概率$p$可以表示如下：

$$h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}$$

其中$g(z)$函数就是sigmoid函数，也叫logistic函数，目的主要是将加权后的特征向量分数压缩到0-1之间。

注：sigmoid函数属于非线性函数，其导数可表示为：

$$g'(z)=g(z)(1-g(z))$$

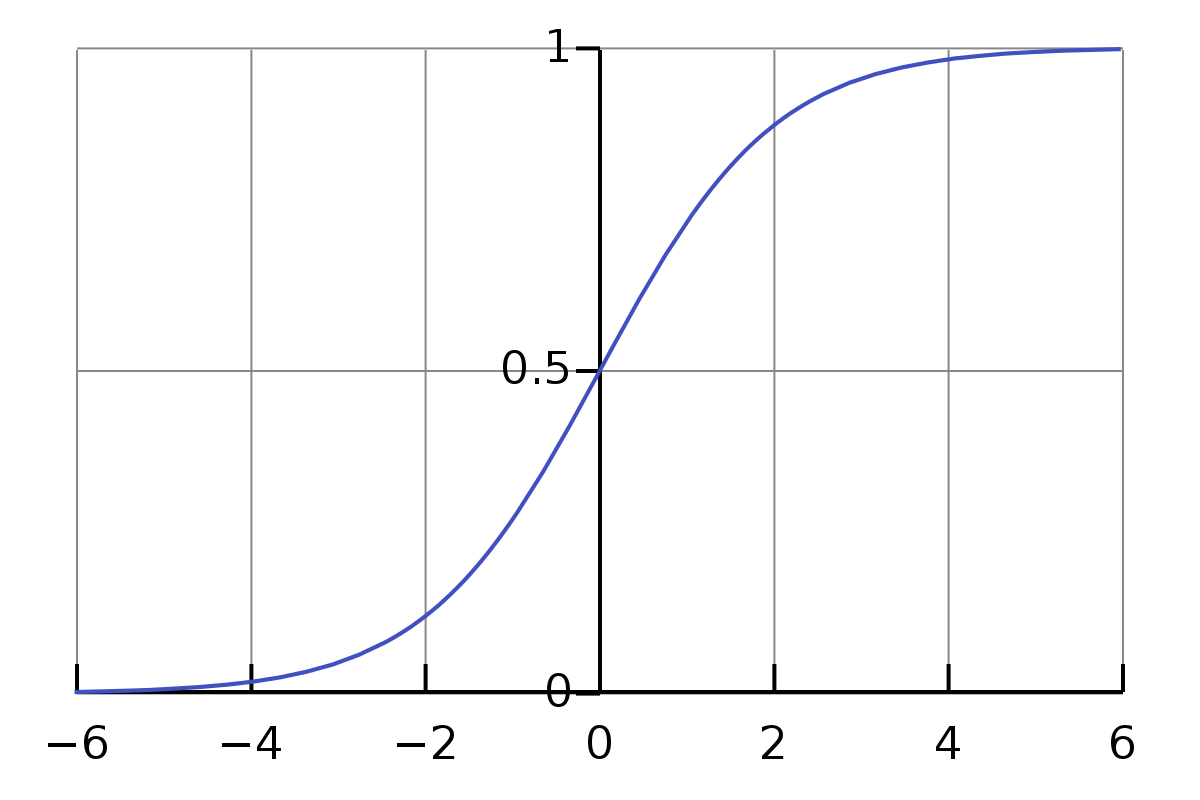
2、逻辑回归虽然使用了非线性函数sigmoid，但因其决策边界$\theta^Tx=0$是一个线性平面，所以逻辑回归本质上属于线性模型。

（三）策略

1、极大似然估计：利用已知的样本结果信息（$x_iy_i$对），反推最有可能导致这些样本结果产生的模型参数（$\theta$）。

2、根据逻辑回归的模型，可得其似然损失：

$$L(\theta)=-\frac{1}{m}\sum_{i=1}^m{log[h_\theta(x_i)^{y_i}(1-h_\theta(x_i))^{(1-y_i)}}]\\=-\frac{1}{m}\sum_{i=1}^m{[y_i log h_\theta(x_i)+(1-y_i)log(1-h_\theta(x_i))}]$$

梯度可表示为：

$$\frac{\partial{L(\theta)}}{\partial{\theta}}=-\frac{1}{m}\sum_{i=1}^m(\frac{y_i}{h_\theta(x_i)}-\frac{1-y_i}{1-h_\theta(x_i)})\frac{\partial{h_\theta(x_i)}}{\partial{\theta}}\\ =-\frac{1}{m}\sum_{i=1}^m(\frac{y_i}{h_\theta(x_i)}-\frac{1-y_i}{1-h_\theta(x_i)})h_\theta(x_i)(1-h_\theta(x_i))x_i \\=-\frac{1}{m}\sum_{i=1}^m(y_i(1-h_\theta(x_i))-(1-y_i)h_\theta(x_i))x_i\\ =-\frac{1}{m}\sum_{i=1}^m(y_i-h_\theta(x_i))x_i$$

注：这儿的loss之所以采用交叉损失而不是均方差，主要是交叉损失带有log，可以化简掉sigmoid里面的指数，从而最后的梯度只跟残差相关，残差越大，梯度越大，训练越快。但是如果是均方差损失的话，化不去sigmoid里面的指数，最后的梯度跟sigmoid的梯度有关，可能存在梯度消失的现象，从而导致训练变慢。

3、为了防止过拟合，可以采用正则化（L1、L2）的手段。
具体体现在似然函数中增加参数的先验，比如对于L1正则，假设参数服从0均值拉普拉斯分布，也就是：

$$p(\theta|u,b)=\frac{1}{2b}e^{-\frac{|\theta-u|}{b}}$$
那么其取log可以表示为：
$$\frac{1}{2b^2}\sum_{j=1}^d|\theta_j|$$
对于L2正则，假设参数服从0均值正态分布，也就是：
$$p(\theta|u,\sigma)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(\theta-u)^2}{2\sigma^2}}$$
那么其取log可以表示为：
$$\frac{1}{2\sigma^2}\sum_{j=1}^d\theta_j^2$$

PS：L1 vs L2：前者的梯度要么是-1要么是1，而后者的梯度是一个直线，越靠近0梯度越小；因此在参数更新过程中，前者是稳步前进，并有可能为更新到0，而后者越更新梯度越小步长也就越小，很难更新到0，这也就是为啥L1更容易稀疏的原因。

二、Softmax模型

（一）简介

1、定义：Softmax模型是逻辑回归模型的一般形式，逻辑回归用于二分类，而Softmax模型用于多分类。

（二）模型

ps：这儿之所以横坐标取值都是负数，原因在于原始的softmax函数，logit值可能会比较大，所以e指数之后会发生溢出，所以一般实现的时候都会对每一个logit减去max（logit）。左右两边取log可以变为：$log(p(y=j|x;\theta))=(logit_j-c)-log\sum_{l=1}^ke^{(logit_l-c)}$，因此该技巧也叫做log-sum-exp技巧。

1、Softmax模型可以表示如下（总共有$k$个类别）：

$$p(y=j|x;\theta)=\frac{e^{\theta_j^Tx}}{\sum_{l=1}^ke^{\theta_l^Tx}}$$

2、当$k=2$时，Softmax模型是可以退化成逻辑回归模型的，一个重要的前提是：

$$p(y=j|x;\theta)=\frac{e^{\theta_j^Tx}}{\sum_{l=1}^ke^{\theta_l^Tx}} \\=\frac{e^{(\theta_j-\theta')^Tx}}{\sum_{l=1}^ke^{(\theta_l-\theta')^Tx}}$$
那么可以假设$\theta'=\theta_1$，因此有：
$$p(y=1|x;\theta)=\frac{e^{(\theta_1-\theta')^Tx}}{\sum_{l=1}^2e^{(\theta_l-\theta')^Tx}} \\=\frac{e^{(\theta_1-\theta_1)^Tx}}{\sum_{l=1}^2e^{(\theta_l-\theta_1)^Tx}} \\=\frac{1}{1+e^{(\theta_2-\theta_1)^Tx}}$$

$$p(y=2|x;\theta)=\frac{e^{(\theta_2-\theta')^Tx}}{\sum_{l=1}^2e^{(\theta_l-\theta')^Tx}} \\=\frac{e^{(\theta_2-\theta_1)^Tx}}{\sum_{l=1}^2e^{(\theta_l-\theta_1)^Tx}} \\=\frac{e^{(\theta_2-\theta_1)^Tx}}{1+e^{(\theta_2-\theta_1)^Tx}} \\=1-\frac{1}{1+e^{(\theta_2-\theta_1)^Tx}}$$

（三）策略

1、【注意代码实现】根据Softmax的模型，可得其似然损失：

$$L(\theta)=-\frac{1}{m}\sum_{i=1}^m{log\prod_{j=1}^k(\frac{e^{\theta_j^Tx_i}}{\sum_{l=1}^ke^{\theta_l^Tx_i}})^{1(y_i=j)}}$$

PS：交叉熵的定义：假设$p$表示样本的真实输出，$q$表示样本的模型输出，那么交叉熵的定义如下：

$$CE = - \frac{1}{m}\sum_xp(x)logq(x)$$
似然损失跟交叉熵最终式子一致。

注：Noise Contrastive Estimation（NCE）vs Negative Sampled Softmax（NEG） vs Hierarchical Softmax（HS）

根据上文可以看出，Softmax模型每一次计算分母都需要遍历所有类别，当分类体系越庞大，计算量越复杂；因此通常会用NCE、NEG、HS等方法来加速计算。
（1）NCE：把softmax的参数估计问题变成一个二分类问题的参数估计，从而避免归一化的计算。二分类中的两类分别是噪声样本和真实样本，具体可以表示为：

$$p(y=0,label_-|context)=\frac{k*q(label_-)}{1+k}\\ p(y=1,label_+|context)=\frac{p(label_+|context;\theta)}{1+k}$$

其中$context$表示进softmax之前的向量，$label$表示预测的类别，$q$表示随机负采样分布，$k$表示负样本数量，$y$表示样本标签。可化简为：

$$p(y=0|context,label_-)=\frac{k*q(label_-)}{p(label_-|context;\theta)+k*q(label_-)}\\ p(y=1|context,label_+)=\frac{p(label_+|context;\theta)}{p(label_+|context;\theta)+k*q(label_-)}$$

那么二分类的loss可以表示为（体现了pairwise的思想）：

$$L(\theta)=\sum_{label_+ \in D}[logp(y=1|context,label_+)+\sum_{label_- \in q}^k log(p(y=0|context,label_-))]$$

（2）NEG：假设$k=|D|$，并且$q$是均匀分布，那么$k*q(label_-)=1$，那么上述可以化简为：

$$p(y=0|context,label_-)=\frac{1}{p(label_-|context;\theta)+1}=1-\frac{1}{1+e^{-s_\theta(context, label_-)}}\\ p(y=1|context,label_+)=\frac{p(label_+|context;\theta)}{p(label_+|context;\theta)+1}=\frac{1}{1+e^{-s_\theta(context, label_+)}}$$

那么其loss就跟二分类的loss是一摸一样的了。

由于NEG的假设前提是$k=|D|$，并且$q$是均匀分布，如果不满足的话（大多数情况是不满足），那么只能近似于softmax（NCE可以证明是等价于softmax）。因此NEG通常用于vector representation的学习，而不用于语言模型的学习（因为对概率的准确输出有要求），NCE多用于语言模型的学习（但相比NEG，NCE会有多余的参数来表示负采样分布，也就是$q(label_-)$）。
（3）HS是为每个类别单独训练一个二分类器，同时通过哈夫曼树将这些分类器进行组织（因此需要各个类别之间存在层级关系的假设，学习效果才会比较好）。

三、FM模型

（一）简介

1、因子分解机(Factorization Machine, FM)是由Steffen Rendle提出的一种基于矩阵分解的机器学习算法。
2、FM主要是解决稀疏数据下的特征组合问题，并且其预测的复杂度是线性的，对于连续和离散特征有较好的通用性。

（二）模型

1、特征组合：将两个特征进行关联之后，可以增加特征跟样本标签的相关性。比如对于“性别”特征以及“商品类型”特征进行关联之后，可以提供更多信息判断用户是否购买。具体做法一般是先将特征分别进行one-hot编码，然后将两个one-hot进行笛卡尔积，就可以得到例如“女性-包包”或者“男性-剃须刀”这样的组合特征，从而可以判断用户是否购买。

2、为了引入组合特征，可以用以下的模型表示：

$$p(y|x;\theta,W)=sigmoid(\theta_0+\sum_{t=1}^{n}\theta_tx^t+\sum_{t=1}^{n-1}\sum_{l=t+1}^{n}w_{tl}x^tx^l)$$
从上述式子可以看出，模型的前半部分是普通的LR线性组合，后半部分的交叉即为特征的组合。其中，$n$代表样本的特征数量，$x^t$代表第$t$个特征，$\theta_0,\theta_t,w_{tl}$是模型参数。组合部分的模型参数$w_{tl}$训练是非常困难的，每个参数$w_{tl}$都需要大量的非零特征$x^t$，$x^l$，由于样本数据本来就比较稀疏，满足“$x^t$，$x^l$同时非零”的样本就更少了，因此训练才困难。

3、为了解决组合部分模型参数训练的困难，FM模型提出了因式分解的方式来解决。对于一个对称矩阵权重参数$W$，可以分解如下：

$$W=VV^T$$
其中$W \in R^{n*n},V \in R^{n*k}$，一般来说，$k$远小于$n$，那么上述的模型可以表示为：
$$p(y|x;\theta,W)=sigmoid(\theta_0+\sum_{t=1}^{n}\theta_tx^t+\sum_{t=1}^{n-1}\sum_{l=t+1}^{n}<v_t, v_l>x^tx^l)$$
$$<v_t, v_l>:=\sum_{f=1}^kv_{t,f}v_{l,f}$$
经过上述的因式分解之后会有几个好处：
（1）参数量减少，本来是$n*n$，现在是$k*n$，其中$k$远小于$n$。
（2）增加特征权重的相关性，比如原先组合特征$x^tx^l$跟$x^tx^{l+1}$的权重参数$w_{tl}$跟$w_{tl+1}$毫无关联，而优化后的权重参数$<v_t, v_l>$跟$<v_t, v_{l+1}>$通过$v_t$产生关联，很大程度可以避免样本稀疏带来的问题。
（3）训练得到的参数$V$可以作为特征的embedding向量。

4、从上述式子来看，FM的前向计算复杂度是$O(kn^2)$，但经过化简，其实复杂度只有$O(kn)$：

$$\sum_{t=1}^{n-1}\sum_{l=t+1}^{n}<v_t, v_l>x^tx^l=\frac{1}{2}(\sum_{t=1}^{n}\sum_{l=1}^{n}<v_t, v_l>x^tx^l-\sum_{t=1}^{n}<v_t, v_t>x^tx^t) \\=\frac{1}{2}(\sum_{t=1}^{n}\sum_{l=1}^{n}\sum_{f=1}^{k}v_{t,f} v_{l,f}x^tx^l-\sum_{t=1}^{n}\sum_{f=1}^{k}v_{t,f} v_{t,f}x^tx^t) \\=\frac{1}{2}\sum_{f=1}^{k}[(\sum_{t=1}^{n}v_{t,f} x^t)(\sum_{l=1}^{n}v_{l,f}x^l)-\sum_{t=1}^{n}v_{t,f}^2{x^t}^2] \\=\frac{1}{2}\sum_{f=1}^{k}[(\sum_{t=1}^{n}v_{t,f} x^t)^2-\sum_{t=1}^{n}{(v_{t,f}x^t)}^2]$$

注：公式的第二步到第三步的依据是：$\sum_i \sum_j U_iI_j=\sum_i U_i \sum_j I_j$。
注：公式的第三步可以理解为对所有的特征embedding向量做累加，然后自己跟自己做内积，等价于第二步的所有特征交叉和；进一步思考，$\sum_{f=1}^{k}(\sum_{t=1}^{n}v_{t,f} x^t)(\sum_{l=1}^{n}v_{l,f}x^l)$可以推算出$\sum_{f=1}^{k}(\sum_{i=1}^{n_1}U_i+\sum_{i=1}^{n_2}I_i+\sum_{i=1}^{n_3}C_i)(\sum_{i=1}^{n_1}U_i+\sum_{i=1}^{n_2}I_i+\sum_{i=1}^{n_3}C_i)$，只考虑有意义的简单交叉也就是$\sum_{f=1}^{k}(\sum_{i=1}^{n_1}U_i)(\sum_{i=1}^{n_2}I_i)$，其实就是分别对用户特征embedding向量以及item特征embedding向量做累加，然后算用户embedding向量跟item embedding向量的内积来表示相似度，相似度越高，代表U-I越为正（这种思路可用于召回层，偏个性化，毕竟是基于特征交叉来做的）（之所以不需要考虑上述第三步括号中的第二项是因为不考虑自己与自己交叉的话，是没有第二项的）；进一步考虑上下文特征的话，那么就是$\sum_{f=1}^{k}(\sum_{i=1}^{n_1}U_i)(\sum_{i=1}^{n_2}I_i)+\sum_{f=1}^{k}(\sum_{i=1}^{n_1}U_i)(\sum_{i=1}^{n_2}C_i)+\sum_{f=1}^{k}(\sum_{i=1}^{n_1}C_i)(\sum_{i=1}^{n_2}I_i)$，注意的是$UC$部分的交叉不影响召回排序。

5、损失函数跟梯度：

损失函数可以表示为：$L(\theta)=-log(\sigma(y^{'}y))$，对应的梯度可以表示为：

$$\frac{\partial{L(\theta)}}{\partial{\theta}}=-\frac{\sigma(y^{'}y)}{\sigma(y^{'}y)}(1-\sigma(y^{'}y))y \frac{\partial{y^{'}}}{\partial{\theta}}$$

其中：对于一阶权重，

$$\frac{\partial{y^{'}}}{\partial{\theta^t}}=x^t$$

对于二阶交叉权重，

$$\frac{\partial{y^{'}}}{\partial{v_{t,f}}}=x_t\sum_{l=1}^nv_{l,f}x^l-v_{t,f}{x^t}^2$$

注：假设$y$的取值为正负1，那么其模型可以表示为：

$$h_\theta(y^{'}y)=g(y^{'}y)=\frac{1}{1+e^{-y\theta^Tx}}$$ ，主要是因为当$y=-1$时， $$1-\frac{1}{1+e^{-\theta^Tx}}=\frac{1}{1+e^{\theta^Tx}}$$

四、FFM模型

（一）简介

1、FFM（Field-aware Factorization Machine）最初的概念来自Yu-Chin Juan（阮毓钦，毕业于中国台湾大学，现在美国Criteo工作）与其比赛队员，是他们借鉴了来自Michael Jahrer的论中的field概念提出了FM的升级版模型。通过引入field的概念，FFM把相同性质的特征归于同一个field。

（二）模型

1、在FFM中，每一维特征$x^t$，针对其它特征的每一种field$f_o$，都会学习一个隐向量 $v_{t,f_o}$。因此，隐向量不仅与特征相关，也与field相关。

2、假设样本的$n$个特征属于$f$个field，那么FFM的二次项有 $nf$个隐向量。而在FM模型中，每一维特征的隐向量只有一个。FM可以看作FFM的特例，是把所有特征都归属到一个field时的FFM模型。根据FFM的field敏感特性，可以导出其模型方程:

$$p(y|x;\theta,W)=sigmoid(\theta_0+\sum_{t=1}^{n}\theta_tx^t+\sum_{t=1}^{n-1}\sum_{l=t+1}^{n}<v_{t,f_l}, v_{l,f_t}>x^tx^l)$$
其中，$f_l$ 是第$l$个特征所属的field。如果隐向量的长度为$k$，那么FFM的二次参数有$nfk$ 个，远多于FM模型的 $nk$ 个。此外，由于隐向量与field相关，FFM二次项并不能够化简，其预测复杂度是 $O(kn^2)$。