@Yeasion-Nein 2018-07-30T12:03:58.000000Z 字数 12294 阅读 1524

网络流 ———— 从零开始（的异世界）

`网络流`

最大流

首先，我们要知道什么是网络流，我们可以类比水流在水管里面的流动，假设在一个类似于有向图中的水管道中，有一个自来水厂 $S$ 点，里面有源源不断的自来水流出，然后在另一个 $T$ 点有一个基饥♂渴的人正在等待着喝水，他已经 $0x7fffffff$ 年没有喝过水啦，所以我们要想办法能让他喝到尽可能多的水。我们知道，每一根管子都有各自的粗♂细，也就是容量，从S点流出的流量不能超过这条路径上的任意一条边的容量，不然管子就会爆掉的。

而求这个人能够喝到的水的最大量就是最大流问题。这个 $S$ 点称为源点，这个 $T$ 点称为汇点，这样的图就叫做网络流。

比如下面这个图的最大流就是 $1$ + $2$ + $2$ = $5$ 。

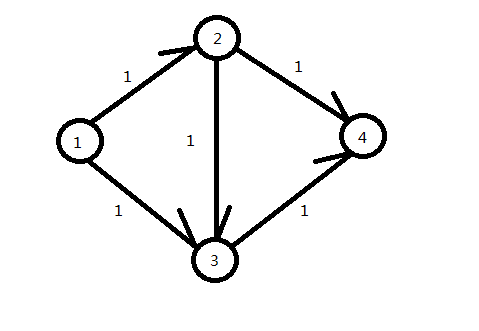
要注意：一个图的最大流路径并不是只有一个（有例外啦），比如上图在上方就是 $1$ ，中间就是 $2$ ，下方也是 $2$ ，然后才总汇成了最大流 $5$ 。

然后是可行流，就是假如所有边上的流量都没有超过容量，那么这一组流称为一组可行流，而很显然，一个网络流的最大流就是所有可行流中流量最大的一种。然后可行流中最简单的就是零流。也就是流量为 $0$ 啦。

然后对于求最大流的算法，这里；列举出了两种：

1： $EK$ 算法 ( $Edmonds-Karp$ )

首先，我们从最简单的零流开始，假设我们搜索到了一条路径 $A$ ，从源点可以到达汇点，即A:{ $S$ -> $a1$ -> $a2$ ->...-> $T$ },然后要注意，这条路上的每一条边满足的条件是流量<容量。并不是<=，因为这样会造成程序死循环。

然后我们可以找到这条路上的每一条边的剩余量的最小值 $rest$ ，就是说我这个流的每一条边都有这 $rest$ 的容量剩余，那么显而易见，我们将这条路上的所有边的流量都加上 $rest$ 仍然是一个可行流。

就这样，我们找到了一个比一开始的流更大的流，也就是之前的流量+ $rest$ ，我们称这条路为增广路。我们从 $S$ 开始不断地寻找增广路，每次增广候我们都会得到一个比原来更大的流。这也就是为什么之前的流量是严格小于容量的，如果是=的话，程序就会一直寻找到 $rest$ 的最小值为 $0$ ，就会形成死循环。

而当找不到增广路的时候，当前的流就是最大流了。

然后具体的算法实现还是有些东西的。举一个已经用烂了的例子来说明吧。

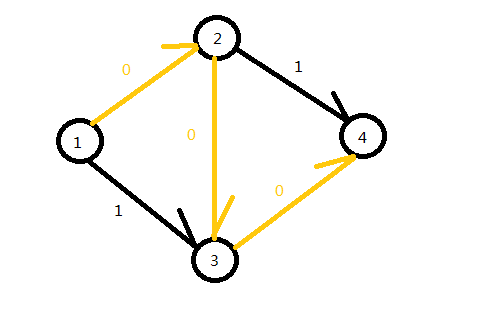
在这里，我们假设傻傻的程序先找到了 $1$ -> $2$ -> $3$ -> $4$ 这条路径，我们就会发现程序找出来的最大流为 $1$ ，然后更改{ $1$ -> $2$ }、{ $2$ -> $3$ }、{ $3$ -> $4$ }的 $rest$ 为 $0$ 。

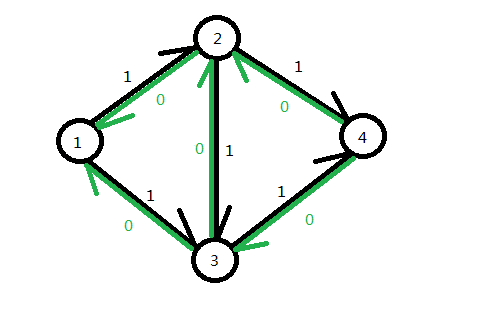
然而我们能很明显的看出来如果流{ $1$ -> $2$ -> $4$ }、{ $1$ -> $3$ -> $4$ }的话，能够得到更大的流量2，于是我们就知道这个程序是有问题的咯。所以我们反思：为什么会出错呢？

答案就是：你可能很聪明，一眼就看出来怎么走，但是程序是傻的，它只会按照你给的机制跑，但是很无奈你并没有给它一个反悔的机制，于是就凉凉了~

在这里我们采用加反向边的做法，对每一条{ $a[i]->a[j]$ }都建一条容量为 $0$ 的反向边{ $a[j]->a[i]$ }。然后整个图建完是这样的：

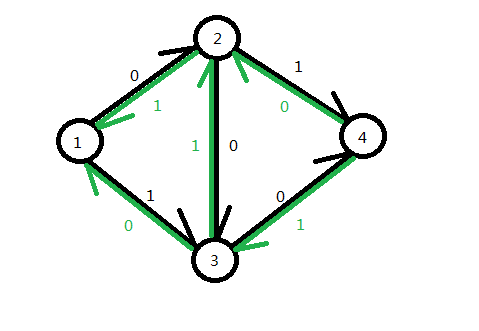
我们在每一次找到增广路的时候会将每一段的容量减少 $rest$ ，同时我们也将这些反向边容量增加 $rest$ 。即：

$cap[a[i]][a[j]]$ -= $rest$ ; $cap[a[j]][a[i]]$ += $rest$ ;

然后按刚才的方法我们先找到了 $1$ -> $2$ -> $3$ -> $4$ ,然后更改.

然后我们再次寻找增广路，找到 $1$ -> $3$ -> $2$ -> $4$ , $rest$ 为 $1$ ，再次增广之后，我们得到了最大流2。就相当与是把流进来的 $2$ -> $4$ 又给退了回去，最后结果就是选了 $1$ -> $2$ -> $4$ 、 $1$ -> $3$ -> $4$ 。这就是原由。

而这个网络流版本就是 $EK$ 算法。

#define MAXN 100010
#define INF 0x7fffffff
bool visit[MAXN];
int pre[MAXN];
queue<int> q;
void update(int now,int rest){
    while(pre[now]){
        map[pre[now]][now]-=rest;//正向的-=rest 
        map[now][pre[now]]+=rest;//负向的+=rest 
        now=pre[now];
    }
}
int find(int S,int T){//寻找增广路流量 
    memset(visit,0,sizeof(visit));
    memset(pre,-1,sizeof(pre));
    visit[S]=1; int minn=INF;
    q.push(S);
    while(!q.empty()){
        int now=q.front(); q.pop();
        if(now==t) break;
        for(int i=1;i<=m;i++){
            if(!visit[i]&&MAP[now][i]){
                q.push(i);
                minn=min(minn,map[now][i]);//最小的rest 
                pre[i]=now; visit[i]=1;
            }
        } 
    }
    if(pre[i]==-1) return 0;
    return minn;
}
int EK(int S,int T){ //EK算法主体 
    int new_flow=0;//增广路的流量 
    int max_flow=0;//最大流 
    do{
        new_flow=find(S,T);
        update(T,new_flow);
        max_flow+=new_flow;
    }while(new_flow);
    return max_flow;
}

恩， $EK$ 算法差不多就是这个样子。

$Dinic$ 算法

首先我们要知道几个重要的基本概念：

$1.cap[u][v]=-cap[v][u]$

$2.∑(p∈E)cap[p][u]==∑(p∈E)cap[u][p]$

而 $Dinic$ 也是基于增广路的思想进行运算的,我们用另一种方式重申一遍增广路的基本步骤

1.找到一条从源点到汇点的路径，使得这条路径上任意一条边的残余流量 $rest$ >0，这条路径便称为增广路。

2.找到这条路径上最小的 $rest$ 为 $minrest$ ，然后将这条路径上的所有边的 $rest$ 减去这个 $minrest$ ,对于我们建的反向边的 $rest$ 都加上这个 $minrest$ 。

重复此上的过程，直到再也找不到增广路，此时我们就找到了最大流。

然后在我们的 $Dinic$ 算法中我们引入分层图的概念，具体就是对于每一个点，我们根据从源点开始的 $BFS$ 序列，给每一个点分配一个 $deep,$ 深度，然后我们进行不断的 $DFS$ 寻找增广路，而每一次我们由 $now$ 推出 $to$ 必须保证 $deep[to]$ == $deep[now]$ + $1;$ 下面是 $Dinic$ 的代码流程。

#define MAXN 100010
#define INF 0x7fffffff
int n,m,s,t;//n:点数，m:边数，s:源点，t:汇点 
struct node{//前向星不解释 
    int from;
    int to;
    int next;
    int rest;//每一条边的剩余流量 
}edge[MAXN*100];
int head[MAXN],total=-1;
void add(int f,int t,int l){
    total++;
    edge[total].from=f;
    edge[total].to=t;
    edge[total].rest=l;
    edge[total].next=head[f];
    head[f]=total;
}
int deep[MAXN];//深度 
queue<int> q;//BFS用队列 
bool bfs(){//bfs用来寻找分层图，增广路 
    while(!q.empty()) q.pop();//清空队列 
    memset(deep,0,sizeof(deep));//清空深度 
    deep[s]=1; q.push(s);//处理源点 
    do{
        int now=q.front(); q.pop();//取队首 
        for(int i=head[now];i!=-1;i=edge[i].next){
            if(edge[i].rest&&!deep[edge[i].to]){
                //如果这条边还有rest并且这个点还没有被发放deep 
                deep[edge[i].to]=deep[now]+1;
                q.push(edge[i].to);//入队列接着bfs 
            }
        }
    }while(!q.empty());
    if(deep[t]==0) return 0;
    //当没有汇点的深度时，说明不存在分层图，也就没有增广路 
    else return 1; //有增广路，可以跑Dinic。 
}
int dfs(int now,int flow){//now：当前节点，flow：当前流量 
    if(now==t||!flow) return flow;
    int res=0;
    for(int i=head[now];i!=-1;i=edge[i].next){
        if(deep[edge[i].to]==deep[now]+1&&edge[i].rest){
        //如果满足分层图并且rest不为0 
            int rest=dfs(edge[i].to,min(flow,edge[i].rest));
            //接着向下dfs。 
            if(rest>0){//增广成功 
                edge[i].rest-=rest;//正向边减去剩余流量 
                edge[i^1].rest+=rest;//负向边加上剩余流量 
                res+=rest;
                flow-=rest;
            }
        }
    }
    return res;//没有增广路的话，就返回0.
}
int Dinic(){
    int ans=0; //用来记录最大流量
    while(bfs()){
        while(int d=dfs(s,INF))
        ans+=d;
    } 
    return ans;
}

然后我们可以在 $Dinic$ 的 $dfs$ 当中进行一个当前弧优化就是说：我们 $DFS$ 的时候不从第一条边开始，用一个数组 $cur$ 记录点 $now$ 之前循环到了那一条边，就可以起到优化的效果，但是要注意：每一次在 $Dinic$ 函数中建立完一次分层图都要把 $cur$ 置为每一个点的第一条边。

#define MAXN 100010
#define INF 0x7fffffff
int n,m,s,t;//n:点数，m:边数，s:源点，t:汇点 
struct node{//前向星不解释 
    int from;
    int to;
    int next;
    int rest;//每一条边的剩余流量 
}edge[MAXN*100];
int head[MAXN],total=-1;
void add(int f,int t,int l){
    total++;
    edge[total].from=f;
    edge[total].to=t;
    edge[total].rest=l;
    edge[total].next=head[f];
    head[f]=total;
}
int cur[MAXN];//这就是那个cur，用来当前弧优化 
int deep[MAXN];//深度 
queue<int> q;//BFS用队列 
bool bfs(){//bfs用来寻找分层图，增广路 
    while(!q.empty()) q.pop();//清空队列 
    memset(deep,0,sizeof(deep));//清空深度 
    deep[s]=1; q.push(s);//处理源点 
    do{
        int now=q.front(); q.pop();//取队首 
        for(int i=head[now];i!=-1;i=edge[i].next){
            if(edge[i].rest&&!deep[edge[i].to]){
                //如果这条边还有rest并且这个点还没有被发放deep 
                deep[edge[i].to]=deep[now]+1;
                q.push(edge[i].to);//入队列接着bfs 
            }
        }
    }while(!q.empty());
    if(deep[t]==0) return 0;
    //当没有汇点的深度时，说明不存在分层图，也就没有增广路 
    else return 1; //有增广路，可以跑Dinic。 
}
int dfs(int now,int flow){//now：当前节点，flow：当前流量 
    if(now==t||!flow) return flow;
    int res=0;
    for(int& i=cur[now];i!=-1;i=edge[i].next){
        //这就是当前弧优化的主要部分，前面的&是为了让cur和i一起变化 
        if(deep[edge[i].to]==deep[now]+1&&edge[i].rest){
        //如果满足分层图并且rest不为0 
            int rest=dfs(edge[i].to,min(flow,edge[i].rest));
            //接着向下dfs。 
            if(rest>0){//增广成功 
                edge[i].rest-=rest;//正向边减去剩余流量 
                edge[i^1].rest+=rest;//负向边加上剩余流量 
                res+=rest;
                flow-=rest;
            }
        }
    }
    return res;//没有增广路的话，就返回0.
}
int Dinic(){
    int ans=0; //用来记录最大流量
    while(bfs()){
        for(int i=1;i<=n;i++)
        cur[i]=head[i];//不要忘了重置 
        while(int d=dfs(s,INF))
        ans+=d;
    } 
    return ans;
}

最大流模板题

$\color{purple}{Link}$

下面放上的是洛谷P3376的网络流模板题，就是为了存个完整代码...

题目描述

如题，给出一个网络图，以及其源点和汇点，求出其网络最大流。

输入输出格式

输入格式：

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含三个正整数ui、vi、wi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi）

输出格式：

一行，包含一个正整数，即为该网络的最大流。

输入样例#1：
4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 40
输出样例#1：
50

样例说明：

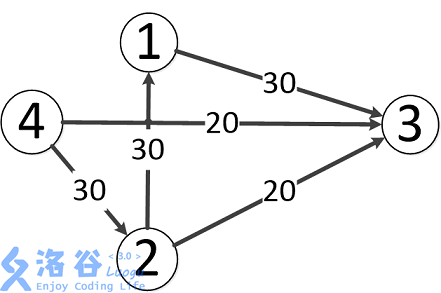
题目中存在3条路径：

4-->2-->3，该路线可通过20的流量

4-->3，可通过20的流量

4-->2-->1-->3，可通过10的流量（边4-->2之前已经耗费了20的流量）

故流量总计20+20+10=50。输出50。

通过证明：

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
#define MAXN 100010
#define INF 0x7fffffff
using namespace std;
int n,m,s,t;//n:点数，m:边数，s:源点，t:汇点 
struct node{//前向星不解释 
    int from;
    int to;
    int next;
    int rest;//每一条边的剩余流量 
}edge[MAXN*100];
int head[MAXN],total=-1;
void add(int f,int t,int l){
    total++;
    edge[total].from=f;
    edge[total].to=t;
    edge[total].rest=l;
    edge[total].next=head[f];
    head[f]=total;
}
int cur[MAXN];//这就是那个cur，用来当前弧优化 
int deep[MAXN];//深度 
queue<int> q;//BFS用队列 
bool bfs(){//bfs用来寻找分层图，增广路 
    while(!q.empty()) q.pop();//清空队列 
    memset(deep,0,sizeof(deep));//清空深度 
    deep[s]=1; q.push(s);//处理源点 
    do{
        int now=q.front(); q.pop();//取队首 
        for(int i=head[now];i!=-1;i=edge[i].next){
            if(edge[i].rest&&!deep[edge[i].to]){
                //如果这条边还有rest并且这个点还没有被发放deep 
                deep[edge[i].to]=deep[now]+1;
                q.push(edge[i].to);//入队列接着bfs 
            }
        }
    }while(!q.empty());
    if(deep[t]==0) return 0;
    //当没有汇点的深度时，说明不存在分层图，也就没有增广路 
    else return 1; //有增广路，可以跑Dinic。 
}
int dfs(int now,int flow){//now：当前节点，flow：当前流量 
    if(now==t||!flow) return flow;
    int res=0;
    for(int& i=cur[now];i!=-1;i=edge[i].next){
        //这就是当前弧优化的主要部分，前面的&是为了让cur和i一起变化 
        if(deep[edge[i].to]==deep[now]+1&&edge[i].rest){
        //如果满足分层图并且rest不为0 
            int rest=dfs(edge[i].to,min(flow,edge[i].rest));
            //接着向下dfs。 
            if(rest>0){//增广成功 
                edge[i].rest-=rest;//正向边减去剩余流量 
                edge[i^1].rest+=rest;//负向边加上剩余流量 
                res+=rest;
                flow-=rest;
            }
        }
    }
    return res;//没有增广路的话，就返回0.
}
int Dinic(){
    int ans=0; //用来记录最大流量
    while(bfs()){
        for(int i=1;i<=n;i++)
        cur[i]=head[i];//不要忘了重置 
        while(int d=dfs(s,INF))
        ans+=d;
    } 
    return ans;
}
int main(){
    scanf("%d%d%d%d",&n,&m,&s,&t);
    for(int i=1;i<=n;i++)   head[i]=-1;
    for(int i=1;i<=m;i++){
        int x,y,l;
        scanf("%d%d%d",&x,&y,&l);
        add(x,y,l);
        add(y,x,0);
    }
    printf("%d",Dinic());
    return 0;
}

最小费用最大流

最小费用最大流的意思其实也很简单，我们现在已经知道最大流是什么了，而我们知道网络流的可行流有很多，而最大流也是不只有一个，题目在每一条边上设定了两个属性：1.cap流量，2.cost费用，要我们输出所有最大流方案中的最小费用。而最小费用最大流和最大费用最大流统称费用流。那么接下来是最小费用最大流的完整的题目描述。

题目描述

如题，给出一个网络图，以及其源点和汇点，每条边已知其最大流量和单位流量费用，求出其网络最大流和在最大流情况下的最小费用。

输入输出格式

输入格式：

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含四个正整数ui、vi、wi、fi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi），单位流量的费用为fi。

输出格式：

　一行，包含两个整数，依次为最大流量和在最大流量情况下的最小费用。＃

大家还记得我们在讲解最大流的时候讲过一种叫做 $EK$ 的算法吧，下面我们来回顾一下：

若一条从源点SS到汇点TT的路径上各条边的剩余容量都大于00，则称这条路径为一条增广路。显然，可以让一股流沿着增广路从SS流到TT，使网络的流量增大。

Edmonds-Karp 算法的思想就是不断用BFS寻找增广路，直至网络上不存在增广路为止。

在每轮寻找增广路的过程中，Edmonds-Karp 算法只考虑图中所有 $f(x,y)<c(x,y)$ 的边，用 $BFS$ 找到任意一条从 $S$ 到 $T$ 的路径，同时计算出路径上各边的剩余容量的最小值 $minf$ ，则网络的流量就可以增加 $minf$ 。

需要注意的是，当一条边的流量 $f(x,y)>0$ 时，根据斜对称性质，它的反向边流量 $f(x,y)<0$ ，此时必有 $f(y,x)<c(y,x)$ 。故 $Edmonds$ - $Karp$ 算法在 BFS时除了原图的边集 $E$ 之外，还应该考虑遍历 $E$ 中每条边的反向边。

在具体实现时，可以按照邻接表成对存储的技巧，把网络的每条有向边及其反向边存在邻接表下标相邻的两个位置，可以相互用xor\1xor得到。并且每条边只记录剩余容量 $c-f$ 即可。当一条边 $(x,y)$ 流过大小为 $e$ 的流时，令 $(x,y)$ 的剩余流量减少 $e$ , $(y,x)$ 的剩余流量增大 $e$ 。

$Edmonds$ - $Karp$ 算法的时间复杂度为 $O(n⋅m^2)$ ，在实际应用中则远远达不到这个上界，效率较高，一般能够处理 $10^3$ 至 $10^4$ 规模的网络。

那么我们接下来要讲解的最小费用最大流也是利用 $EK$ 算法来解决的，首先，我们沿着最短路进行增广，而路径长度自然就是路径上的费用，而我们建的反向边的费用是对应正向边的费用的相反数（为了保证过程可逆），而反向边的流量像往常一样依然是0。这里我们可以选择用 $SPFA$ 或者是 $Dijkstra$ 进行最短路，然后就是求解最短路的实际流量并修改相关数据，以便下一次在残余网络上继续进行增广。

说到这里可能会有些懵逼，不要急，我会先通过更简单易懂的语言来讲解，然后我们还会结合代码慢慢的讲。

其实我们要想：最小费用最大流比单纯的最大流多了什么？就是一个路径上的费用，那我们要解决的就是这个费用问题，那么我们要求得最小的费用要用的最好懒的方法是什么呢？当然就是最短路啊，我们知道 $EK$ 算法有一个 $BFS()$ 函数，我们也知道 $SPFA$ 和 $Dijkstra$ 这种最短路求法也是 $BFS$ ，那么我们就可以很愉快地将 $BFS$ 函数转化为最短路的算法啦~。

下面我们结合着代码讲解一下：

首先我们来介绍一下下面要用到的变量的名称：

int n,m,s,t;
//n:点数,m:边数,s:起点,t:终点
int dist[MAXN],flow[MAXN];
//dist[i]:从s到i的最短路径长度(SPFA用)
//flow:流量
bool inque[MAXN];;
//inque[i]表示点i是否在队列里面。
int pre[MAXN],rest[MAXN];
//pre[i]:i的前驱节点
//rest[i]第i条边的剩余流量
int max_flow; int min_spent;
//max_flow:最大流
//min_spent:最小花费
queue<int> q;
//队列

加边没有什么问题。

struct node{
    int from;
    int to;
    int len;
    //费用 
    int cap;
    //流量 
    int next;
}edge[MAXN];
int head[MAXN],total=-1;
//要注意将这里的head[MAXN]和total都置为-1！Yeasion在这上面摔了好几次 
void add(int f,int t,int l,int c){
    total++;
    edge[total].from=f;
    edge[total].to=t;
    edge[total].len=l;
    edge[total].cap=c;
    edge[total].next=head[f];
    head[f]=total;
}

然后主函数颇为稀松，但是要注意建反向边的时候要将流量置为0，将费用置为原正向边的相反数（ $edge[i].cap=-edge[i$ ^ $1].cap$ ）。

int main(){
    scanf("%d%d%d%d",&n,&m,&s,&t);
    for(int i=1;i<=n;i++) head[i]=-1;
    for(int i=1;i<=m;i++){
        int x; int y; int l; int c;
        scanf("%d%d%d%d",&x,&y,&c,&l);
        add(x,y,l,c); add(y,x,0,-c);
        //注意加反向边要注意的两点哦
    } Edmonds_Karp(s,t);
    printf("%d %d",max_flow,min_spent);
    return 0;
}

接下来就是 $EK$ 函数了，我们在这个函数里面传入了begin和end的参数，如果大家不想传递的话是可以省略掉的

void Edmonds_Karp(int begin,int end){
    while(SPFA(begin,end)){
        //寻找增广路 
        int now=end;
        max_flow+=rest[end];
        //将最大流加上最小流量 
        min_spent+=dist[end]*rest[end];
        //将最小花费加上从s开始到t的最小路径长*到t的最小流量 
        while(now!=begin){
            edge[last[now]].cap-=rest[end];
            //正向边减去最小流量 
            edge[last[now]^1].cap+=rest[end];
            //反向边加上最小流量 
            now=pre[now];
            //设置前趋 
        }
    }
}

最后是SPFA的函数，在这里面我们主要进行的操作有三个：1.找出最短路。当然这个最短路的前提条件是每一条边都有剩余流量edge[i].cap，不然没有任何意义。2.寻找最小流量rest。3.寻找每一个点的前驱。然后返回的条件依然是看有没有找到增广路，就是看t的前驱有没有被更新如果没有，自然就是没有任何一条路能够到达t节点。

bool SPFA(int begin,int end){
    while(!q.empty()) q.pop();
    memset(dist,127,sizeof(dist));
    memset(inque,0,sizeof(inque));
    memset(rest,127,sizeof(rest));
    //每一次的SPFA不要忘了将所有的变量还原 
    //但千万别还原pre qwq 
    q.push(begin); inque[begin]=1;
    //入队s点 ，初始化 
    pre[end]=-1; dist[begin]=0;
    //SPFA过程 
    while(!q.empty()){
        int now=q.front();q.pop();
        inque[now]=false;
        for(int i=head[now];i!=-1;i=edge[i].next)
            if(edge[i].cap>0)//这里就是网络流的部分了，首先这条边如果没有了残余流量我们肯定不跑 
            if(dist[edge[i].to]>dist[now]+edge[i].len){
                dist[edge[i].to]=dist[now]+edge[i].len;//SPFA松弛操作 
                pre[edge[i].to]=now;//更新edge[i].to的前驱为now 
                rest[edge[i].to]=min(rest[now],edge[i].cap);
                //寻找最小的流量 
                if(!inque[edge[i].to]){//入队，继续SPFA 
                    q.push(edge[i].to);
                    inque[edge[i].to]=1;
                }
            }
    }
    if(pre[end]==-1) return 0;
    //如果没有找到t即：t的前驱依然是不存在的-1，则没有增广路，返回0，停止EK 
    else return 1; //继续进行EK 
}

下面是 $EK$ 的算法代码：

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
#define MAXN 100010
#define INF 0x7fffffff
#define ll long long
using namespace std;
int n,m,s,t;
struct node{
    int from;
    int to;
    int len;
    int cap;
    int next;
}edge[MAXN];
int head[MAXN],total=-1;
void add(int f,int t,int l,int c){
    total++;
    edge[total].from=f;
    edge[total].to=t;
    edge[total].len=l;
    edge[total].cap=c;
    edge[total].next=head[f];
    head[f]=total;
}
int dist[MAXN],flow[MAXN];
bool inque[MAXN]; int last[MAXN];
int pre[MAXN],rest[MAXN];
int max_flow; int min_spent;
queue<int> q;
bool SPFA(int begin,int end){
    while(!q.empty()) q.pop();
    memset(dist,127,sizeof(dist));
    memset(inque,0,sizeof(inque));
    memset(rest,127,sizeof(rest));
    q.push(begin); inque[begin]=1;
    pre[end]=-1; dist[begin]=0;
    while(!q.empty()){
        int now=q.front();q.pop();
        inque[now]=false;
        for(int i=head[now];i!=-1;i=edge[i].next)
            if(edge[i].cap>0)
            if(dist[edge[i].to]>dist[now]+edge[i].len){
                dist[edge[i].to]=dist[now]+edge[i].len;
                pre[edge[i].to]=now;
                last[edge[i].to]=i;
                rest[edge[i].to]=min(rest[now],edge[i].cap);
                if(!inque[edge[i].to]){
                    q.push(edge[i].to);
                    inque[edge[i].to]=1;
                }
            }
    }
    if(pre[end]==-1) return 0;
    else return 1;
}
void Edmonds_Karp(int begin,int end){
    while(SPFA(begin,end)){
        int now=end;
        max_flow+=rest[end];
        min_spent+=dist[end]*rest[end];
        while(now!=begin){
            edge[last[now]].cap-=rest[end];
            edge[last[now]^1].cap+=rest[end];
            now=pre[now];
        }
    }
}
int main(){
    scanf("%d%d%d%d",&n,&m,&s,&t);
    for(int i=1;i<=n;i++) head[i]=-1;
    for(int i=1;i<=m;i++){
        int x; int y; int l; int c;
        scanf("%d%d%d%d",&x,&y,&c,&l);
        add(x,y,l,c); add(y,x,0,-c);
    } Edmonds_Karp(s,t);
    printf("%d %d",max_flow,min_spent);
    return 0;
}

网络流 ———— 从零开始（的异世界）

网络流

最大流

而求这个人能够喝到的水的最大量就是最大流问题。这个S点称为源点，这个T点称为汇点，这样的图就叫做网络流。

比如下面这个图的最大流就是1+2+2=5。

要注意：一个图的最大流路径并不是只有一个（有例外啦），比如上图在上方就是1，中间就是2，下方也是2，然后才总汇成了最大流5。

然后是可行流，就是假如所有边上的流量都没有超过容量，那么这一组流称为一组可行流，而很显然，一个网络流的最大流就是所有可行流中流量最大的一种。然后可行流中最简单的就是零流。也就是流量为0啦。

然后对于求最大流的算法，这里；列举出了两种：

1：EK算法 (Edmonds-Karp)

首先，我们从最简单的零流开始，假设我们搜索到了一条路径A，从源点可以到达汇点，即A:{S->a1->a2->...->T},然后要注意，这条路上的每一条边满足的条件是流量<容量。并不是<=，因为这样会造成程序死循环。

然后我们可以找到这条路上的每一条边的剩余量的最小值rest，就是说我这个流的每一条边都有这rest的容量剩余，那么显而易见，我们将这条路上的所有边的流量都加上rest仍然是一个可行流。

而当找不到增广路的时候，当前的流就是最大流了。

然后具体的算法实现还是有些东西的。举一个已经用烂了的例子来说明吧。

在这里，我们假设傻傻的程序先找到了1->2->3->4这条路径，我们就会发现程序找出来的最大流为1，然后更改{1->2}、{2->3}、{3->4}的rest为0。

然而我们能很明显的看出来如果流{1->2->4}、{1->3->4}的话，能够得到更大的流量2，于是我们就知道这个程序是有问题的咯。所以我们反思：为什么会出错呢？

答案就是：你可能很聪明，一眼就看出来怎么走，但是程序是傻的，它只会按照你给的机制跑，但是很无奈你并没有给它一个反悔的机制，于是就凉凉了~

在这里我们采用加反向边的做法，对每一条{a[i]->a[j]}都建一条容量为0的反向边{a[j]->a[i]}。然后整个图建完是这样的：

我们在每一次找到增广路的时候会将每一段的容量减少rest，同时我们也将这些反向边容量增加rest。即：

cap[a[i]][a[j]]-=rest; cap[a[j]][a[i]]+=rest;

然后按刚才的方法我们先找到了1->2->3->4,然后更改.

然后我们再次寻找增广路，找到1->3->2->4,rest为1，再次增广之后，我们得到了最大流2。就相当与是把流进来的2->4又给退了回去，最后结果就是选了1->2->4、1->3->4。这就是原由。

而这个网络流版本就是EK算法。

恩，EK算法差不多就是这个样子。

Dinic算法

首先我们要知道几个重要的基本概念：

1.cap[u][v]=-cap[v][u]

2.∑(p∈E)cap[p][u]==∑(p∈E)cap[u][p]

而Dinic也是基于增广路的思想进行运算的,我们用另一种方式重申一遍增广路的基本步骤

1.找到一条从源点到汇点的路径，使得这条路径上任意一条边的残余流量rest>0，这条路径便称为增广路。

2.找到这条路径上最小的rest为minrest，然后将这条路径上的所有边的rest减去这个minrest,对于我们建的反向边的rest都加上这个minrest。

重复此上的过程，直到再也找不到增广路，此时我们就找到了最大流。

最大流模板题

下面放上的是洛谷P3376的网络流模板题，就是为了存个完整代码...

题目描述

如题，给出一个网络图，以及其源点和汇点，求出其网络最大流。

输入输出格式

输入格式：

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含三个正整数ui、vi、wi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi）

输出格式：

一行，包含一个正整数，即为该网络的最大流。

样例说明：

题目中存在3条路径：

4-->2-->3，该路线可通过20的流量

4-->3，可通过20的流量

4-->2-->1-->3，可通过10的流量（边4-->2之前已经耗费了20的流量）

故流量总计20+20+10=50。输出50。

通过证明：

最小费用最大流

题目描述

如题，给出一个网络图，以及其源点和汇点，每条边已知其最大流量和单位流量费用，求出其网络最大流和在最大流情况下的最小费用。

输入输出格式

输入格式：

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含四个正整数ui、vi、wi、fi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi），单位流量的费用为fi。

输出格式：

一行，包含两个整数，依次为最大流量和在最大流量情况下的最小费用。＃

大家还记得我们在讲解最大流的时候讲过一种叫做EK的算法吧，下面我们来回顾一下：

若一条从源点SS到汇点TT的路径上各条边的剩余容量都大于00，则称这条路径为一条增广路。显然，可以让一股流沿着增广路从SS流到TT，使网络的流量增大。

Edmonds-Karp 算法的思想就是不断用BFS寻找增广路，直至网络上不存在增广路为止。

在每轮寻找增广路的过程中，Edmonds-Karp 算法只考虑图中所有 f(x,y)<c(x,y)的边，用BFS找到任意一条从S到T的路径，同时计算出路径上各边的剩余容量的最小值minf，则网络的流量就可以增加minf。

需要注意的是，当一条边的流量f(x,y)>0时，根据斜对称性质，它的反向边流量f(x,y)<0，此时必有f(y,x)<c(y,x)。故Edmonds-Karp算法在 BFS时除了原图的边集E之外，还应该考虑遍历E中每条边的反向边。

Edmonds-Karp算法的时间复杂度为O(n⋅m^2)，在实际应用中则远远达不到这个上界，效率较高，一般能够处理 10^3至10^4规模的网络。

说到这里可能会有些懵逼，不要急，我会先通过更简单易懂的语言来讲解，然后我们还会结合代码慢慢的讲。

下面我们结合着代码讲解一下：

首先我们来介绍一下下面要用到的变量的名称：

加边没有什么问题。

然后主函数颇为稀松，但是要注意建反向边的时候要将流量置为0，将费用置为原正向边的相反数（edge[i].cap=-edge[i^1].cap）。

接下来就是EK函数了，我们在这个函数里面传入了begin和end的参数，如果大家不想传递的话是可以省略掉的

下面是EK的算法代码：

内容目录

`网络流`

而求这个人能够喝到的水的最大量就是最大流问题。这个 $S$ 点称为源点，这个 $T$ 点称为汇点，这样的图就叫做网络流。

比如下面这个图的最大流就是 $1$ + $2$ + $2$ = $5$ 。

要注意：一个图的最大流路径并不是只有一个（有例外啦），比如上图在上方就是 $1$ ，中间就是 $2$ ，下方也是 $2$ ，然后才总汇成了最大流 $5$ 。

然后是可行流，就是假如所有边上的流量都没有超过容量，那么这一组流称为一组可行流，而很显然，一个网络流的最大流就是所有可行流中流量最大的一种。然后可行流中最简单的就是零流。也就是流量为 $0$ 啦。

1： $EK$ 算法 ( $Edmonds-Karp$ )

首先，我们从最简单的零流开始，假设我们搜索到了一条路径 $A$ ，从源点可以到达汇点，即A:{ $S$ -> $a1$ -> $a2$ ->...-> $T$ },然后要注意，这条路上的每一条边满足的条件是流量<容量。并不是<=，因为这样会造成程序死循环。

然后我们可以找到这条路上的每一条边的剩余量的最小值 $rest$ ，就是说我这个流的每一条边都有这 $rest$ 的容量剩余，那么显而易见，我们将这条路上的所有边的流量都加上 $rest$ 仍然是一个可行流。

在这里，我们假设傻傻的程序先找到了 $1$ -> $2$ -> $3$ -> $4$ 这条路径，我们就会发现程序找出来的最大流为 $1$ ，然后更改{ $1$ -> $2$ }、{ $2$ -> $3$ }、{ $3$ -> $4$ }的 $rest$ 为 $0$ 。

然而我们能很明显的看出来如果流{ $1$ -> $2$ -> $4$ }、{ $1$ -> $3$ -> $4$ }的话，能够得到更大的流量2，于是我们就知道这个程序是有问题的咯。所以我们反思：为什么会出错呢？

在这里我们采用加反向边的做法，对每一条{ $a[i]->a[j]$ }都建一条容量为 $0$ 的反向边{ $a[j]->a[i]$ }。然后整个图建完是这样的：

我们在每一次找到增广路的时候会将每一段的容量减少 $rest$ ，同时我们也将这些反向边容量增加 $rest$ 。即：

$cap[a[i]][a[j]]$ -= $rest$ ; $cap[a[j]][a[i]]$ += $rest$ ;

然后按刚才的方法我们先找到了 $1$ -> $2$ -> $3$ -> $4$ ,然后更改.

然后我们再次寻找增广路，找到 $1$ -> $3$ -> $2$ -> $4$ , $rest$ 为 $1$ ，再次增广之后，我们得到了最大流2。就相当与是把流进来的 $2$ -> $4$ 又给退了回去，最后结果就是选了 $1$ -> $2$ -> $4$ 、 $1$ -> $3$ -> $4$ 。这就是原由。

而这个网络流版本就是 $EK$ 算法。

恩， $EK$ 算法差不多就是这个样子。

$Dinic$ 算法

$1.cap[u][v]=-cap[v][u]$

$2.∑(p∈E)cap[p][u]==∑(p∈E)cap[u][p]$

而 $Dinic$ 也是基于增广路的思想进行运算的,我们用另一种方式重申一遍增广路的基本步骤

1.找到一条从源点到汇点的路径，使得这条路径上任意一条边的残余流量 $rest$ >0，这条路径便称为增广路。

2.找到这条路径上最小的 $rest$ 为 $minrest$ ，然后将这条路径上的所有边的 $rest$ 减去这个 $minrest$ ,对于我们建的反向边的 $rest$ 都加上这个 $minrest$ 。

　一行，包含两个整数，依次为最大流量和在最大流量情况下的最小费用。＃

大家还记得我们在讲解最大流的时候讲过一种叫做 $EK$ 的算法吧，下面我们来回顾一下：

在每轮寻找增广路的过程中，Edmonds-Karp 算法只考虑图中所有 $f(x,y)<c(x,y)$ 的边，用 $BFS$ 找到任意一条从 $S$ 到 $T$ 的路径，同时计算出路径上各边的剩余容量的最小值 $minf$ ，则网络的流量就可以增加 $minf$ 。

需要注意的是，当一条边的流量 $f(x,y)>0$ 时，根据斜对称性质，它的反向边流量 $f(x,y)<0$ ，此时必有 $f(y,x)<c(y,x)$ 。故 $Edmonds$ - $Karp$ 算法在 BFS时除了原图的边集 $E$ 之外，还应该考虑遍历 $E$ 中每条边的反向边。

$Edmonds$ - $Karp$ 算法的时间复杂度为 $O(n⋅m^2)$ ，在实际应用中则远远达不到这个上界，效率较高，一般能够处理 $10^3$ 至 $10^4$ 规模的网络。

然后主函数颇为稀松，但是要注意建反向边的时候要将流量置为0，将费用置为原正向边的相反数（ $edge[i].cap=-edge[i$ ^ $1].cap$ ）。

接下来就是 $EK$ 函数了，我们在这个函数里面传入了begin和end的参数，如果大家不想传递的话是可以省略掉的

下面是 $EK$ 的算法代码：