@Wayne-Z
2017-11-05T07:27:12.000000Z
字数 3728
阅读 5505
Data Lab: Manipulating Bits
ssd6
Environment
- vscode
- gcc
Analisis
This project need we use just 8 operators to finish 10 puzzles. So lets review these 8 operators and their uses as follows.
- '!' logical operation NOT
- '~' bit level operation NOT
- '&' bit level operation AND
- '^' bit level operation EXCLUSIVE-OR
- ' | ' bit level operation OR
- '+' arithmatical plus
- '<<' left shift
- '>>' arithmatical right shift for signed number in the implemantation, logical right shift for unsigned number
Then we can take a look at this puzzles, we can know the basic idea for many problems is to find the combination of those operators that has equivalent truth values of the expected outcomes.
Puzzles
bitAnd(x,y)
/** bitAnd - x&y using only ~ and |* Example: bitAnd(6, 5) = 4* Legal ops: ~ |* Max ops: 8* Rating: 1*/int bitAnd(int x, int y) {return ~(~x|~y);}
For this function, we just need to look at the true value table and find a equivalent way.
| x | y | x&y | ~x | ~y | ~(~x |~y) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 |
bitOr(x,y)
/** bitOr - x|y using only ~ and &* Example: bitOr(6, 5) = 7* Legal ops: ~ &* Max ops: 8* Rating: 1*/int bitOr(int x, int y) {return ~(~x&~y);}
similarly, we just need to look at the truth value table.
| x | y | x | y | ~x | ~y | ~(~x&~y) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 |
isZero()
/** isZero - returns 1 if x == 0, and 0 otherwise* Examples: isZero(5) = 0, isZero(0) = 1* Legal ops: ! ~ & ^ | + << >>* Max ops: 2* Rating: 1*/int isZero(int x) {return !x;}
This function just need we to use logical not, if x is zero, then x means false, !x is true.
minusOne
/** minusOne - return a value of -1* Legal ops: ! ~ & ^ | + << >>* Max ops: 2* Rating: 1*/int minusOne(void) {return ~0;}
This time we need the bit operation not. We can know that signed integer 0 in binary expression is all 0 in each bit, so use ~ we get all 1 which is -1 in decimal.
TMax
/** TMax - return maximum two's complement integer* Legal ops: ! ~ & ^ | + << >>* Max ops: 4* Rating: 1*/int tmax(void) {return ~(1<<31);}
to find the max integer in two's complement, we know it is 0x7fffffff, we just need 0x1 left shift 31 bit to get 0x80000000, and use bit level not to make it all 1 except the first bit.
bitXor
/** bitXor - x^y using only ~ and &* Example: bitXor(4, 5) = 1* Legal ops: ~ &* Max ops: 14* Rating: 2*/int bitXor(int x, int y) {return ~(~(~x&y)&~(x&~y));}
It is more compicated than the former, but we still need to use the truth value table.
| x | y | x ^ y | ~x | ~y | (~x&y) | (x&~y) | (~x&y)|(x&~y) |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
However, '|' is not allowed, so we need to use bitOr again thuse we get ~(~(~x&y)&~(x&~y)).
getByte
/** getByte - Extract byte n from word x* Bytes numbered from 0 (LSB) to 3 (MSB)* Examples: getByte(0x12345678,1) = 0x56* Legal ops: ! ~ & ^ | + << >>* Max ops: 6* Rating: 2*/int getByte(int x, int n) {return (x>>(n<<3)&(0xff);}
This time, we need to use a mask to get the exact byte we need. First we move bits to the start of the byte, we need move 8*n bit, which is equal to n<<3, then we just need a mask has 8 bits' 1, which is 0xff, and use & to mask them. We can also use mask first, but since right shift is arithmatic shift as we mentioned before, it may get some bugs since we need both shift the mask and the number if x is negative.
isEqual
/** isEqual - return 1 if x == y, and 0 otherwise* Examples: isEqual(5,5) = 1, isEqual(4,5) = 0* Legal ops: ! ~ & ^ | + << >>* Max ops: 5* Rating: 2*/int isEqual(int x, int y) {return !(x^y);}
What we need to do is using bit level exclusive not to compare their bits to check whether they are equal, and use logical not to check if there are bits that is 1. We can use the truth value table.
| x | y | x ^ y | !(x^y) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
negate
/** negate - return -x* Example: negate(1) = -1.* Legal ops: ! ~ & ^ | + << >>* Max ops: 5* Rating: 2*/int negate(int x) {return ~x+1;}
We can know that the definetion of twos complement. So we just need to take the back and plus 1.
isPositive
/** isPositive - return 1 if x > 0, return 0 otherwise* Example: isPositive(-1) = 0.* Legal ops: ! ~ & ^ | + << >>* Max ops: 8* Rating: 3*/int isPositive(int x) {return !(x>>31)&(!(!(x&(0x7FFFFFFF))));}
This take some time for some cases. First we need to right shift 31 bits to check its sign bit. If it is positive, x>>31 get all 0, but if x is not, x<31 get all 1. And since x should bigger than 0, so we still need (x&(0x7FFFFFFF)) to ensure x is not 0;
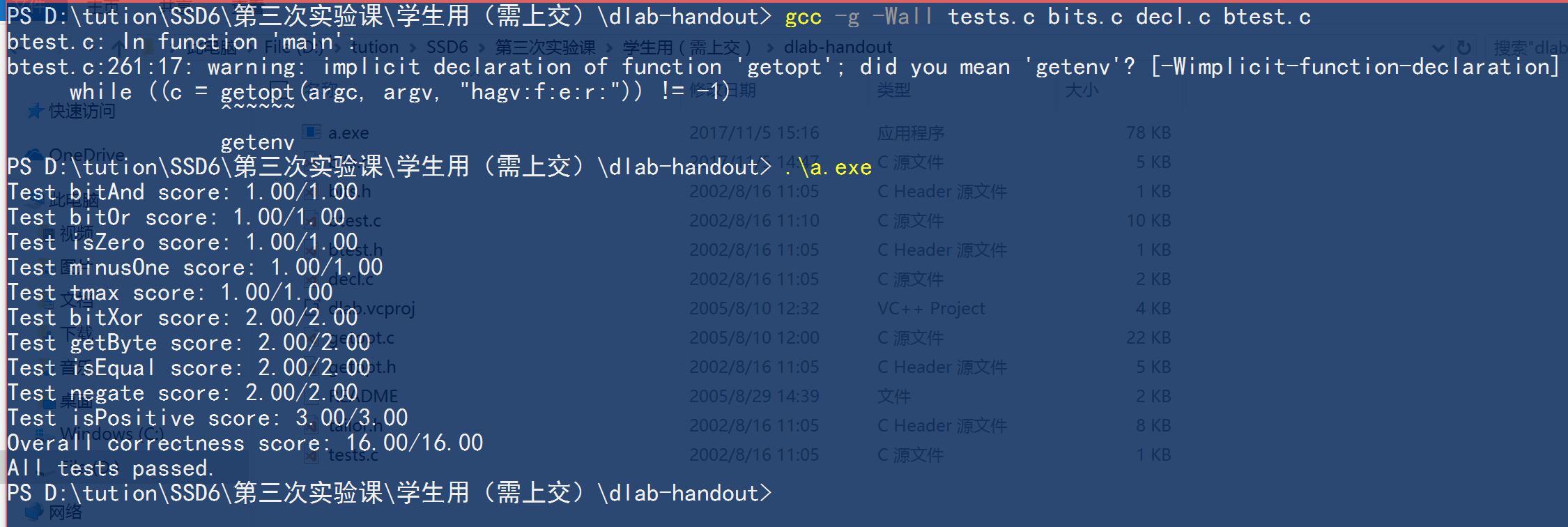
Outcom
After compilation, we can run the program for test, we can see it passes all tests.