关于KNN和K-means算法的学习报告

KNNK-means

---

KNN:

KNN 算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性

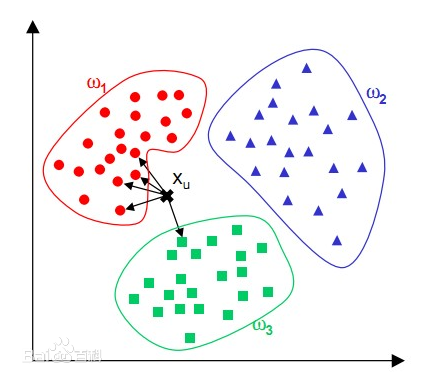
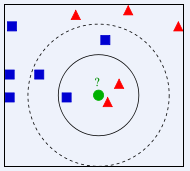
伪代码：

计算测试数据与各个训练数据之间的距离；
按照距离的递增关系进行排序；
选取距离最小的K个点；
确定前K个点所在类别的出现频率；
返回前K个点中出现频率最高的类别作为测试数据的预测分类

训练参数：

dataset16.mat\fourclass

实现代码(Python)：

KNN_Algorithm:

#coding=utf-8
__anthor__='Haoyang Li'
'''KNN算法的实现，时间复杂度O(n)
样本数据集采用datesaet16.mat中的fourclass'''
import numpy as np
import matplotlib.pyplot as plt
import scipy.io as sio
import math
import operator
d = sio.loadmat('dataset16.mat')
data = (d['fourclass'])
x, y = data[:, 1], data[:, 2]  # 样本的两个特征x
xy_set = np.array([np.reshape(x,len(x)),np.reshape(y,len(y))]).transpose()
label = data[:, 0]  # 对应的标签y
def Knn_Algorithm(input=([0,0.5]),k=3):
    # 计算输入点据样本中各个点的距离
    data_num = data.shape[0]
    diff_xy = np.tile(input,(data_num,1))-xy_set
    diff_xy_2 = diff_xy ** 2
    dist_2 = diff_xy_2[:, 0] + diff_xy_2[:, 1]
    #另一种操作：dist_2 = np.sum(cha_xy_2,axis=1)
    distance = dist_2 ** 0.5
    #对距离进行排序
    sorted_index = np.argsort(distance)
    #对所属类别进行统
    cluster_cnt = {}
    for i in range(k):
        to_label = label[sorted_index[i]]
        if 'to_label' in cluster_cnt.keys():
            cluster_cnt[to_label] += 1
        else:
            cluster_cnt[to_label] = 1
        # 更好的操作：cluster_cnt[to_label] = cluster_cnt.get(to_label,0)+1
    #遍历一次得出结果
    max = 0
    for key,value in cluster_cnt.items():
        if(value) > max:
            result = key
    return  result
#print (Knn_Algorithm())

测试代码：

#coding=utf-8
import  sys
import  numpy as np
sys.path.append(r"C:\Users\54164\PycharmProjects\K-Algorithm")
import KNN_Algorithm
input = np.array([0.34,0.32])
k=3
output = KNN_Algorithm.Knn_Algorithm(input,k)
print("测试数据为：",input,"分类结果为:",output)

实验结果：

K-means:

K-means算法是硬聚类算法，是典型的基于原型的目标函数聚类方法的代表，它是数据点到原型的某种距离作为优化的目标函数，利用函数求极值的方法得到迭代运算的调整规则。K-means算法以欧式距离作为相似度测度，它是求对应某一初始聚类中心向量V最优分类，使得评价指标J最小。算法采用误差平方和准则函数作为聚类准则函数。

算法步骤

1.Initialize cluster centroids(初始化聚类中心)

$$\mu_1,\mu_2\cdots\mu_k\in R^n$$
2.repeat till convergence(重复下面步骤直到收敛)
i) $$c^{i}:=arg\min \limits_{j}\left \| x^{i}-\mu_j \right \|^2$$
ii) $$\mu_j:=\frac{\sum_{i=1}^m1\left\{ \ c^{i} = j \right\}x^{i}}{\sum_{i=1}^m1\left\{ \ c^{i} = j \right\}}$$

伪代码：

随机选择k个点作为初始聚类中心；
当任意一个点的簇分配结果发生改变时：
  对数据集中的每一个数据点：
    对每一个质心：
      计算质心与数据点的距离
    将数据点分配到距离最近的簇
  对每一个簇，计算簇中所有点的均值，并将均值作为质心

训练参数：

dateset16.mat\kmeans_test

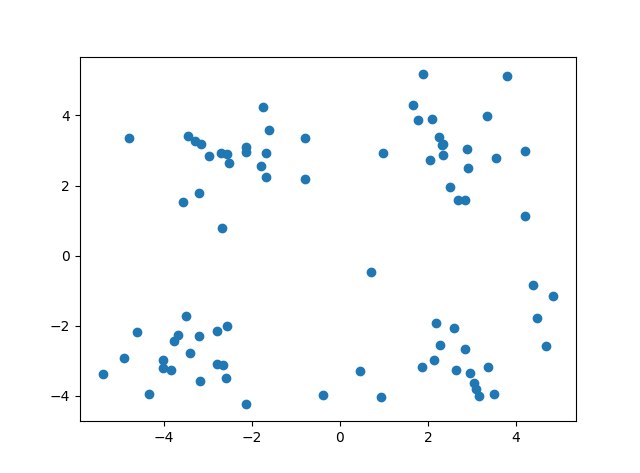
实现代码(Python)：

#coding=utf-8
__anthor__='Haoyang Li'
'''K-means算法的实现
样本数据集采用datesaet16.mat中的svmguide1'''
import numpy as np
import time
import matplotlib.pyplot as plt
import scipy.io as sio
import math
d = sio.loadmat('dataset16.mat')
data = (d['kmeans_test'])
#x, y = data[:, 0], data[:, 1]
#计算欧式距离(Euclidean distance)
def eucl_distance(vec_1,vec_2):
    return math.sqrt(np.sum(np.power(vec_1-vec_2,2)))
#s随机初始化聚类中心(inicialize centroids)
def init_centroids(data_set,k):
    data_num,dimension = data_set.shape
    centroids = np.zeros((k,dimension))
    for i in range(k):
        index = int(np.random.uniform(0,data_num))
        centroids[i,:] = data_set[index,:]
    return  centroids
def k_means(data_set,k):
    data_num = data_set.shape[0]
    clus_assiment = np.zeros((data_num, 1))
    clus_adjusted = True
    #初始化聚类
    centroids = init_centroids(data_set,k)
    while clus_adjusted:
        clus_adjusted=False
        #对于每个样本
        for i in range(data_num):
            min_dist = 1000000
            min_index = 0
            #对于每个聚类中心
            for j in range(k):
                #找到最近的聚类
                distance = eucl_distance(centroids[j,:],data_set[i,:])
                if distance < min_dist:
                    min_dist = distance
                    min_index = j
            #更新点的聚类
            if clus_assiment[i,0] != min_index:
                clus_adjusted = True
                clus_assiment[i] = min_index
        #更新聚类
        for j in range(k):
            points = data_set[np.nonzero(clus_assiment[:, 0] == j)[0]]
            centroids[j, :] = np.mean(points, axis=0)
    print('K-means聚类完成~')
    #绘图
    colors = ['b', 'g', 'r', 'k', 'c', 'm', 'y', '#e24fff', '#524C90', '#845868']
    for i in range(data_num):
        mark_index = int(clus_assiment[i,0])
        plt.scatter(data_set[i,0],data[i,1],color=colors[mark_index])
    plt.show()

测试代码：

#coding=utf-8
import  sys
import scipy.io as sio
import  numpy as np
sys.path.append(r"C:\Users\54164\PycharmProjects\K-Algorithm")
import K_means
d = sio.loadmat('dataset16.mat')
data = (d['kmeans_test'])
k=4
K_means.k_means(data,k)

实验结果：

总结：

KNN	K-means
1.KNN是分类算法 2.监督学习 3.喂给它的数据集是带label的数据，已经是完全正确的数据	1.K-means是聚类算法 2.无监督学习
没有明显的前期训练过程，属于memory-based learning	有明显的前期训练过程
K的含义：来了一个样本x，要给它分类，即求出它的y，就从数据集中，在x附近找离它最近的K个数据点，这K个数据点，类别c占的个数最多，就把x的label设为c	K的含义：K是人工固定好的数字，假设数据集合可以分为K个簇，由于是依靠人工定好，需要一点先验知识

The End