10.24 solution

Jewel Splitting

哈希的各种技巧…
对于每个 $d$ ，恰好有 $n/d$ 个子段：前缀 +后缀。计算所有前缀子段与后缀子段的哈希值，并离散化（为了方便维护集合的哈希值，转化为序列哈希）。枚举前缀，可以动态维护每种子段的出现次数。为了去重，也需要维护集合的哈希值。使用哈希表维护得到更优的时间复杂度，总共需要写四个不同的哈希。时间复杂度为 $O(n \log n)$ 。

Holy Sequence

考察对于计数 DP 的熟悉程度，以及对于组合意义的运用。
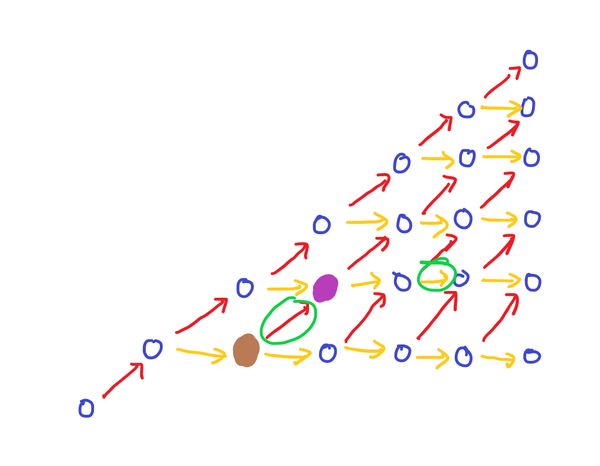
考虑第二类斯特林数的 DP 方程： $s[i][j]=s[i-1][j-1]+s[i-1][j]*j$ ，给它找一个组合意义。如果转移为 $s[i-1][j-1]$ ，表示新增了一个数 $j+1$ 。如果转移为 $s[i-1][j]*j$ 表示新增一个 $[1,j]$ 中的数 $x$ 。可以发现任意一个合法序列都恰好被统计一次。

DP 的转移是一个 DAG，那么 DP 可以看做是 DAG 的路径计数，发现合法序列与从 $(0,0)$ 到 $(n,j)$ 的路径一一对应。转移边分为两类，这里用不同的颜色标记。
假设数字 $k$ 在合法序列中出现了 $x$ 次，贡献为 $x^2$ 。 可以考虑组合意义，表示在 $x$ 个 $k$ 中选择两次的方案数。分两类情况：两次都选择在了同一个位置上，或者选择了不同的位置。这里只考虑选择两个不同的位置怎么处理。

不同的转移边对应不同的决策（什么位置放什么数），由于某个数第二次出现之后一定不是前缀最大值，就只能是黄色转移边了。
一种情况如上图所示，就需要求出经过这两条转移边的路径数量。可以从左往右DP $(0,0)$ 到棕色点的路径数量，从右往左DP $(n,j)$ 到紫色点的数量（附加状态：是否选择了某条转移边）。
另一种情况就是左侧的转移边为黄色转移边。这样会对一个前缀的 k 产生贡献，做一个差分就可以了。时间复杂度为 $\mathcal{O}(n^2)$ 。