斯特林数

OI

一个经典套路：求答案的k次方之和。下降幂转成组合数，往往可以做一个多项式快速幂，然后第二类斯特林数还原。

更加一般化的套路：求形如 $(\sum x_i)^k$，可以枚举选择了多少不同的 $x$。

这里的不同 $x$ 往往都是等价的，所以可以一起算。常应用于期望题

CC EASYEX 求 $\prod (\sum a_{i,j})^k$ 的期望。对于每个 $(\sum a_{i,j})^k$，可以枚举出现了多少个相互独立的随机变量。注意到不同的 $\sum$ 乘起来并不是独立的，所以需要把存在多少独立随机变量记录在DP的状态里。这个东西可以用分治NTT优化。

第一类

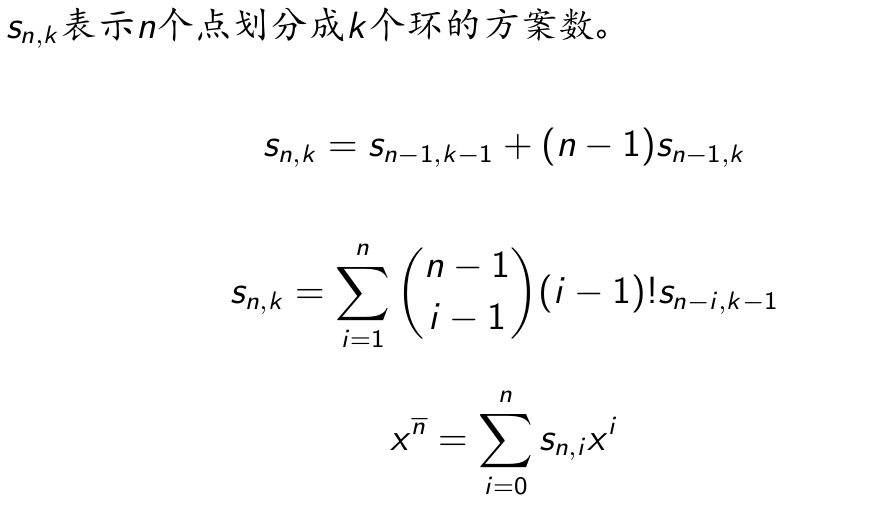
第二类

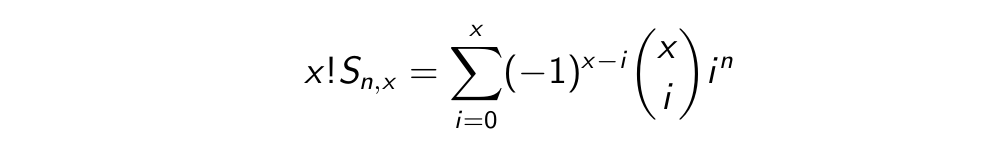
一个应用

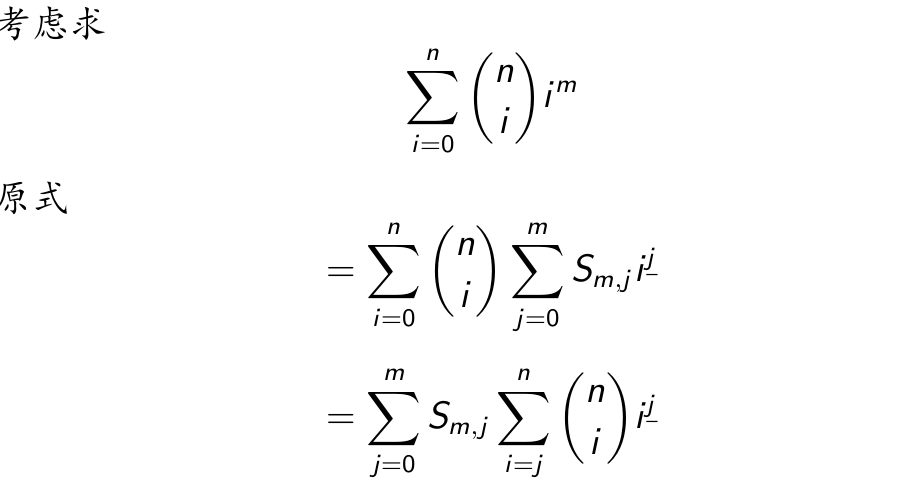
经典题目一

经典题目二