[关闭]
@Catyee 2021-05-28T14:10:00.000000Z 字数 5546 阅读 612

二叉树算法题

数据结构与算法

一、二叉搜索树

二叉搜索数的一个重要特性：中序遍历是升序的

leetcode 230 二叉搜索树中第k小的数

  1. int result = Integer.MIN_VALUE;
  2. int current = 0;
  3. public int kthSmallest(TreeNode root, int k) {
  4.     calKthSmallest(root, k);
  5.     return result;
  6. }
  8. public void calKthSmallest(TreeNode root, int k) {
  9.     if (root == null || result != Integer.MIN_VALUE) {
  10.         return;
  11.     }
  12.     calKthSmallest(root.left, k);
  13.     if (++current == k) {
  14.         result = root.val;
  15.     }
  16.     calKthSmallest(root.right, k);
  17. }

利用中序遍历升序的特点进行遍历，当遍历到第k个节点的时候就是要找的节点，不用再继续遍历了。

leetcode 538 转化累加树

给出二叉搜索树的根节点，该树的节点值各不相同，将该树转化为累加树，使新树的每个节点的新值等于原树中大于或等于node.val的值的和。

  1. TreeNode last = null;
  2. public TreeNode convertBST(TreeNode root) {
  3.     convert(root);
  4.     return root;
  5. }
  7. public void convert(TreeNode root) {
  8.     if (root == null) {
  9.         return;
  10.     }
  11.     convert(root.right);
  12.     int newVal = root.val;
  13.     if (last != null) {
  14.         newVal += last.val;
  15.     }
  16.     root.val = newVal;
  17.     last = root;
  18.     convert(root.left);
  19. }

下图是leetcode中给出的示例：
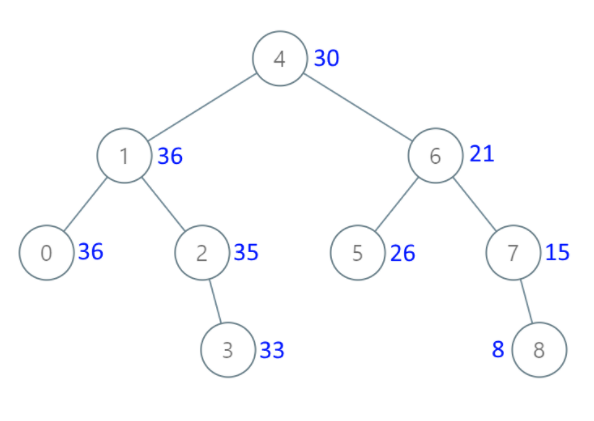
1、leetcode538示例
由于要处理每个节点的值，每个节点都要访问到，所以总是要进行树的遍历的，树的遍历就只有前序、中序、后序、层次这四种，不妨把遍历顺序和最终结果都写出来找找规律，这里就只写中序遍历的结果了：

节点原值 0 1 2 3 4 5 6 7 8
最终值 36 36 35 33 30 26 21 15 8

发现了吗？当前节点的最终值是下一个节点的最终值+当前节点的原值，如果我们将中序反过来，也就是说先遍历右子树，然后访问当前节点，再访问左子树，那么当前节点的最终值就是上一个访问的节点的最终值+当前节点的原值，我们只需要一个额外的节点记录上一次访问的节点就可以了。

leetcode 98 验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

二叉搜索树是这样一棵树，如果左子树不为空，则左子树的所有节点的值都小于根节点，如果右子树不为空，则右子树的所有节点都大于根节点，同时左子树和右子树也都是二叉搜索树。
根据题目的意思，我们很可能将代码写成如下的样子：

  1. public boolean isVaildBST(TreeNode root) {
  2.     if (root == null) {
  3.         return true;
  4.     }
  5.     if (root.left != null && root.left.val >= root.val) {
  6.         return false;
  7.     } 
  8.     if (root.right != null && root.right.val <= root.val) {
  9.         return false;
  10.     }
  11.     return isVaildBST(root.left) && isVaildBST(root.right);
  12. }

但是要注意！！二叉搜索树的根节点大于所有左子树节点，小于所有右子树节点，并不仅仅是大于左子树的根节点，也不仅仅是小于右子树的根节点。上面这段代码只是比较了根节点和左孩子右孩子的值，这是不够的。比如这样一棵树：

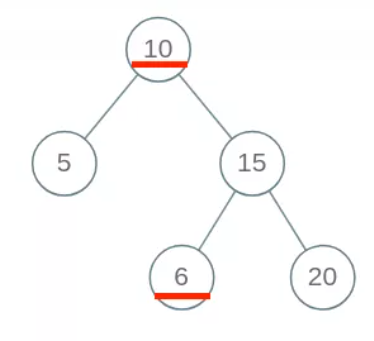
2、leetcode98错误的树
这棵树显然不是一棵二叉搜索树，但是上面的代码将返回true。
正确的做法就是在递归的时候传入子树节点的取值范围来加强约束：

  1. public boolean isVaildBST(TreeNode root) {
  2.     return isVaildBST(root, null, null);
  3. }
  5. public boolean isVaildBST(TreeNode root, TreeNode min, TreeNode max) {
  6.     if (root == null) {
  7.         return true;
  8.     }
  9.     if (min != null && min.val >= root.val) {
  10.         return false;
  11.     }
  12.     if (max != null && max.val <= root.val) {
  13.         return false;
  14.     }
  15.     return isVaildBST(root.left, min, root) && isVaildBST(root.right, root, max);
  16. }

leetcode 701 二叉搜索树中的插入操作

二叉搜索树的插入操作是比较简单的，因为最终插入的位置总是叶子节点的位置。

  1. public TreeNode insertIntoBST(TreeNode root, int val) {
  2.     if (root == null) {
  3.         return new TreeNode(val);
  4.     }
  5.     insert(root, val);
  6.     return root;
  7. }
  9. public void insert(TreeNode root, int val) {
  10.     if (val < root.val) {
  11.         if (root.left != null) {
  12.             insert(root.left, val);
  13.         } else {
  14.             TreeNode node = new TreeNode(val);
  15.             root.left = node;
  16.         }
  17.     } else if (val > root.val) {
  18.         if (root.right != null) {
  19.             insert(root.right, val);
  20.         } else {
  21.             TreeNode node = new TreeNode(val);
  22.             root.right = node;
  23.         }
  24.     } else {
  25.         throw new RuntimeException("unexpect error");
  26.     }
  27. }

leetcode 450 删除二叉搜索树中的节点

删除二叉树的节点要比插入麻烦许多，因为一个节点直接删除之后可能会破坏二叉搜索树的性质，所以要考虑清楚如何删除：
有三种情况：

三种情况分析完了之后我们看"删除节点"这个行为，如果"被删除的节点"有父节点，则需要将父节点原来指向"被删除节点"的指针指向替代它的节点，同时将"被删除节点"的左右孩子置为空，还要保证替代它的节点左右指针的指向也要正确。如果被删除的节点没有父节点，则说明被删除的节点就是根节点。

小技巧：在上面第三种情况中："删除节点，然后用左子树的最大值或者右子树的最小值代替它的位置"可以进一步简化，这里以左子树的最大值为例，只要把左子树的最大值赋给"待删除的节点"，然后删掉左子树最大值所在的节点，由于左子树最大值所在的节点要么是叶子节点，要么是右孩子为空的节点，所以第三种情况转化为了前两种情况。
代码：

  1. /**
  2. * deleteNode方法的定义：删除二叉搜索树中的一个节点，然后返回删除之后树的根节点
  3. * 要记住这个定义，递归的时候不要陷入递归栈中，而应该把握递归方法的定义，相信这个方法能完成的工作
  4. */
  5. public TreeNode deleteNode(TreeNode root, int key) {
  6.     if (root == null) {
  7.         return null;
  8.     }
  9.     if (key == root.val) { // 相等表示root即使要删除的节点
  10.         /* 处理左右孩子有空节点的情况，也就是上面列举的前两种情况 */
  11.         if (root.left == null) {
  12.             return root.right;
  13.         }
  14.         if (root.right == null) {
  15.             return root.left;
  16.         }
  17.         /* 处理左右孩子节点都不为空的情况，也就是上面列举的第三种情况 */
  18.         TreeNode leftMaxNode = getMaxNode(root.left); 
  19.         // 把左子树的最大值赋给待删除的节点
  20.         root.val = leftMaxNode.val; 
  21.         // 在左子树中删除左子树最大值所在的节点，相信deleteNode方法的定义，所以返回的是删除之后左子树的根节点，重新连接上
  22.         root.left = deleteNode(root.left, leftMaxNode.val); 
  23.     } else if (key < root.val) {
  24.         // 到左子树上去删除，相信deleteNode方法的定义，所以返回的是删除之后左子树的根节点，重新连接上
  25.         root.left = deleteNode(root.left, key); 
  26.     } else if (key > root.val) {
  27.         // 到右子树上去删除，相信deleteNode方法的定义，所以返回的是删除之后右子树的根节点，重新连接上
  28.         root.right = deleteNode(root.right, key); 
  29.     }
  30.     return root;
  31. }
  33. private TreeNode getMaxNode(TreeNode root) {
  34.     while (root.right != null) {
  35.         root = root.right;
  36.     }
  37.     return root;
  38. }

这种实现优雅、巧妙，但是如果真实的开发环境，可能每个节点都有着复杂的值，“赋值操作”反而麻烦，进行引用的操作反而简单，下面提供修改引用的方式：

  1. /**
  2. * deleteNode方法的定义：删除二叉搜索树中的一个节点，然后返回删除之后树的根节点
  3. * 要记住这个定义，递归的时候不要陷入递归栈中，而应该把握递归方法的定义，相信这个方法能完成的工作
  4. */
  5. public TreeNode deleteNode(TreeNode root, int key) {
  6.     if (root == null) {
  7.         return null;
  8.     }
  9.     if (key == root.val) {
  10.         /* 处理左右孩子有空节点的情况，也就是上面列举的前两种情况 */
  11.         if (root.left == null) {
  12.             return root.right;
  13.         }
  14.         if (root.right == null) {
  15.             return root.left;
  16.         }
  17.         /* 处理左右孩子节点都不为空的情况，也就是上面列举的第三种情况 */
  18.         TreeNode leftMaxNode = getMaxNode(root.left);
  19.         leftMaxNode.left = deleteNode(root.left, leftMaxNode.val);
  20.         leftMaxNode.right = root.right;
  21.         root.left = null; 
  22.         root.right = null; 
  23.         // 用左子树最大值所在节点替换要删除的节点，所以返回的也是左子树最大值所在节点
  24.         return leftMaxNode; 
  25.     } else if (key < root.val) {
  26.         root.left = deleteNode(root.left, key);
  27.     } else if (key > root.val) {
  28.         root.right = deleteNode(root.right, key);
  29.     }
  30.     return root;
  31. }
  33. private TreeNode getMaxNode(TreeNode root) {
  34.     while (root.right != null) {
  35.         root = root.right;
  36.     }
  37.     return root;
  38. }

非递归的实现方式：

  1. private TreeNode parrent = null;
  2. private TreeNode node = null; 
  3. public TreeNode deleteNode(TreeNode root, int key) {
  4.     findNode(root, key);
  5.     if (node == null) {
  6.         return root;
  7.     }
  8.     TreeNode current = null;
  9.     if (node.left != null && node.right != null) {
  10.         current = findAndDeleteLeftMax(node.left);
  11.         if (current != node.left) {
  12.             current.left = node.left;
  13.         }
  14.         current.right = node.right;
  15.     } else {
  16.         current = node.left == null ? node.right : node.left;
  17.     }
  18.     node.left = null;
  19.     node.right = null;
  20.     if (parrent == null) {
  21.         return current;
  22.     }
  23.     if (parrent.left == node) {
  24.         parrent.left = current; 
  25.     }
  26.     if (parrent.right == node) {
  27.         parrent.right = current;
  28.     }
  29.     return root;
  30. }
  32. public TreeNode findAndDeleteLeftMax(TreeNode root) {
  33.     TreeNode last = null;
  34.     while (root.right != null) {
  35.         last = root;
  36.         root = root.right;
  37.     }
  38.     if (last != null) {
  39.         last.right = root.left;
  40.         root.left = null;
  41.     }
  42.     return root;
  43. }
  45. public void findNode(TreeNode root, int key) {
  46.     if (root == null || node != null) {
  47.         return;
  48.     }
  49.     if (root.val == key) {
  50.         node = root;
  51.         return;
  52.     }
  53.     if (key < root.val) {
  54.         parrent = root;
  55.         findNode(root.left, key); 
  56.     }
  57.     if (key > root.val) {
  58.         parrent = root;
  59.         findNode(root.right, key);
  60.     }
  61. }
添加新批注
在作者公开此批注前，只有你和作者可见。
回复批注