对于群论与生成函数的重新整理

群论

---

定义

群G是一个定义在二元组$(S,\cdot)$的代数结构
$S$是一个集合," $\cdot$ "是一个二元运算，比如"$+,-,*,/$",与集合的运算中的$∪\ ∩$
满足下列条件的二元组$G=(S,\cdot)$可以为群
一对元素，一个运算，满足封闭性，集合率，幺元存在唯一/x + x = x/ ，逆元存在唯一

1.封闭性

$\forall x,y∈S,x·y∈S$
就是集合$S$中任意取两个元素，他们

置换是排列

置换

对于置换f(x)和置换g(x)的乘积，就是f(g(x))
也就是上图先做左边，再做右边
置换群就是置换的集合

Burnside引理：
在某个置换下不变的值就是

生成函数

形式幂级数

泰勒展开

在某个点附近把一个函数展开成一个无限项的多项式
比如：等比数列求和

$$\sum_{i = 0}^{inf} = \frac{1}{1-x}$$

广义牛顿二项式定理

$$(x + y)^n = \sum_{k=0}^{inf}C(n,k)x^{n-k}y^k$$
其中
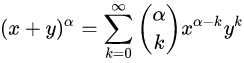这是形式上的组合数

形式幂级数

对于一个序列$a_i$
定义一个$A(x)=\sum_{i=0}^{inf}a_ix^i$

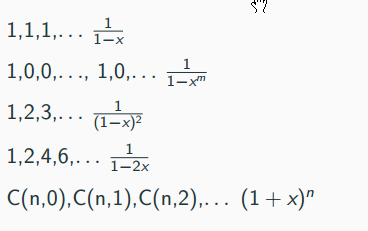
生成函数能干啥

生成函数整题可以做多项式运算。
生成函数的乘法相当于两个集合的组合
还可以用生成函数来解一类组合问题
还能用来求通项

例子：
斐波那契数列
$f_n = f_{n-1}+f_{n-2}$
构造斐波那契数列生成函数
$F(x) = \sum_{i=0}^{inf}f_ix^i$
$xF(x) = 0 + 1x + 1x^2+2x^3+3x^4+5x^5+...$
$x^2F(x) =0 + 0x + 1x^2+1x^3+2x^4+3x^5$
做差得到
$(1-x-x^2)A=1$那么$A=\frac{1}{1-x-x^2}$
我们构造了两个生成函数解出了斐波那契数列的通项

*x能让整个生成函数后退一次
下式-1为空项

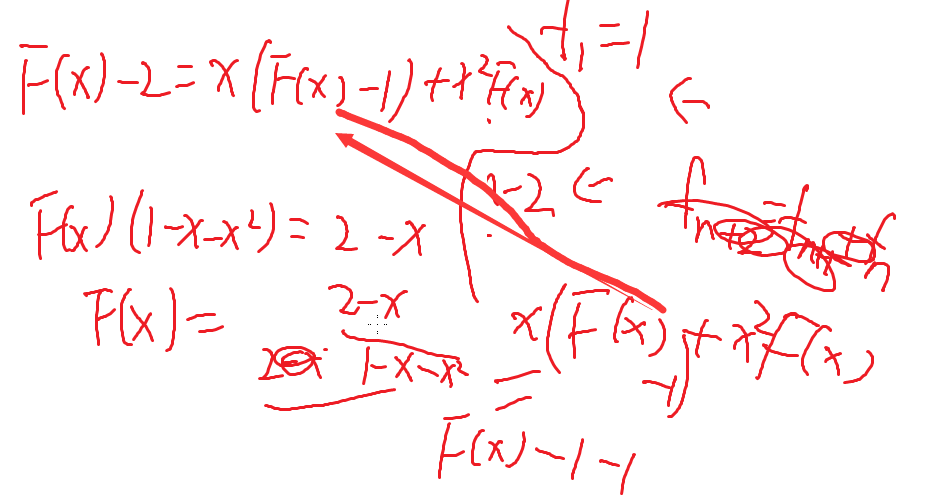
然后我们得到的就是一个组合的问题

指数型生成函数

也就是每个地下除一个i！
这样定义出来的就是指数生成函数

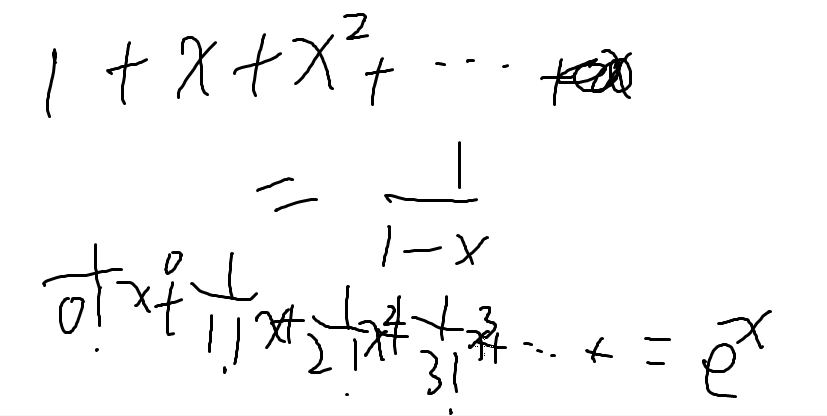
对于两个指数型生成函数相乘

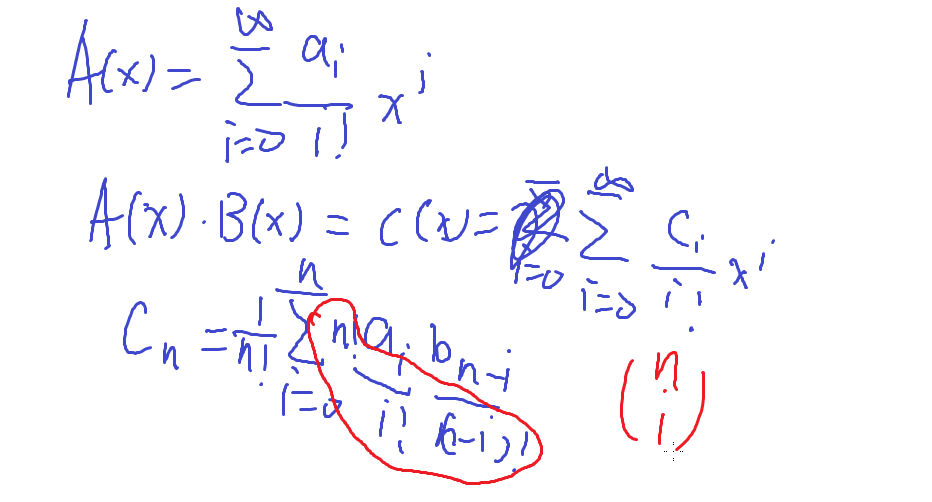
指数型生成函数C就是

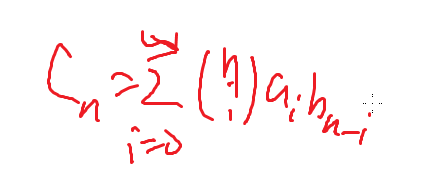
然后我们得到的是一个排列的问题

简单反演