零基础微积分入门基本教程

微积分

---

$$\lim_{学习 \to 坚持} 学习 = 成功$$

前言

非常高兴你能浏览到这篇文章。
我也不太清楚我写作的动机，可能纯属兴趣使然吧。

参考书籍

1. 《高等数学（第六版）》上册
   同济大学数学系 编
   高等教育出版社 出版
2. 《7 天搞定微积分》
   石山平 大上丈彦 著 李巧丽 译
   南海出版公司 出版
3. 《Principles of Mathematical Analysis》
   Walter Rudin 著
   McGraw-Hill Education 出版

我是否适合看下去？

在看这篇文章前，你至少需要掌握以下知识：
1. 至少初中水平的数学应用能力
2. 至少小学水平的阅读能力
3. 耐心和对数学的热情
4. 以上三条是扯淡
5. 这条也是

What’s calculus?

在正式开始学习微积分前，首先我们得明白微积分是啥。
百度一下，我们很容易找到这样的描述：

微积分（Calculus）是高等数学中研究函数的微分、积分以及有关概念和应用的数学分支。它是数学的一个基础学科。
内容主要包括极限、微分学、积分学及其应用。
微分学包括求导数的运算，是一套关于变化率的理论。
它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。
积分学，包括求积分的运算，为定义和计算面积、体积等提供一套通用的方法。

诶诶诶，别跑啊，我知道这种专家写出来的东西不是一般人能领会得了的。。

简单的说，微积分学是高等数学(并不是高中数学)的重要组成部分，它的地位，相当于小学的四则运算或是初中的方程运算。它非常奇怪、麻烦，可是在高等数学中，你时时刻刻都要用到它。

当然，人们不会故意发明奇怪、麻烦的东西来为难自己，它的应用十分广泛，我们在后面会慢慢提到。

它主要分成两个部分：微分和积分，它们相辅相成，虽各有变化却互为表里，是一对基佬兄弟。我们会在接下来的文章中分别讨论这两个东西。

废话不多说，马上上干货～～

一。导数

导数是微分学的主要内容。翻回去看看百度百科对导数的解释：

导数描述一个函数的变化率。

这是啥么意思呢？变化率是个什么东西？

1.1 First Blood —— 斜率

先来看个函数图像：

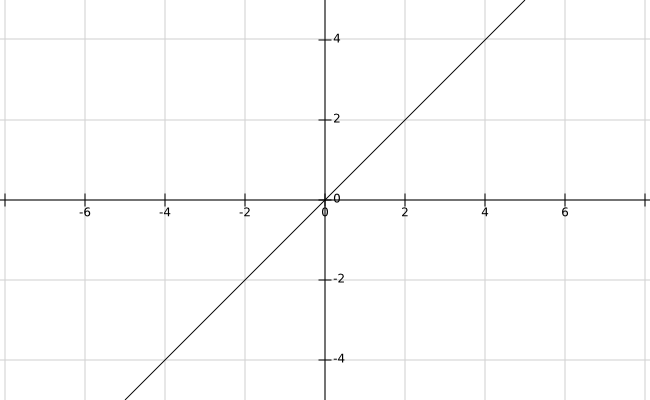
相信你一口就能报出这个函数的解析式：

$$y=x$$
然后，我们再看个稍微复杂点的图像：

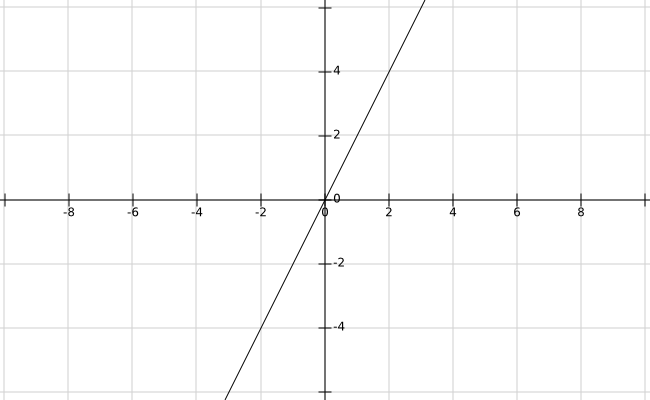
额，这哪里复杂了嘛！明明还是个一次函数啊。。。

不不不，差别大了去了，试试找出这两个函数图像的不同之处？

上下滚动页面，你应当能够看出图像倾斜程度存在着区别，有的数学老师也叫它 $k$决定函数陡平啥啥的。

回忆一次函数的表达式:

$$y = kx+b (k≠0)$$
哈，所以上面这个式子里，$k$ 值的大小就代表着图像倾斜程度的大小，不是吗？

好了，你的头脑中已经有了基本的微分概念了，同学们，下课！

哈哈，开个玩笑，还是先别急着关掉页面(从哪里能找到这么没节操的文章 真是)。
不过这句话并没有问题，应当说，从初中学习函数开始，我们就有了对于这些知识的模糊概念，只是它们尚未发掘出来。所以这篇所谓的教程，其实就是帮助万恶的数学老师解决这些概念问题...

还是回到上面这个简单的例子。我们说$y=x$与$y=2x$这两个函数的倾斜程度不同，因为$y=2x$显得更"陡"一些。

虽然小明同学觉得这样描述很好，但是呢，数学家们就是不满足于"a比b陡"这样听起来不是很清楚(也可能是因为他们语文阅读能力不行)的描述方式，(这样听起来不够炫酷狂霸拽)于是发明了一个很好(奇)听(怪)的名字用来描述一条线的陡峭程度，这就是———— 斜率。

当当！我们终于接触到了第一个数学定义。

呃... 虽说这个定义还不完整，甚至你还没弄清啥意思，不过万事总有个开头的，是吧？

接下来我们将慢慢解释斜率这个听起来很高大上的名词。

既然说斜率是个数值，是数值就应该能被写出来。那么我们怎么表示它呢？

再再一次回到上面的例子。容易发现，当$k=2$时，图像明显比$k=1$时的要陡峭不少。继续画下去：$k=3、4、5、6、7...$
图像会越来越陡。

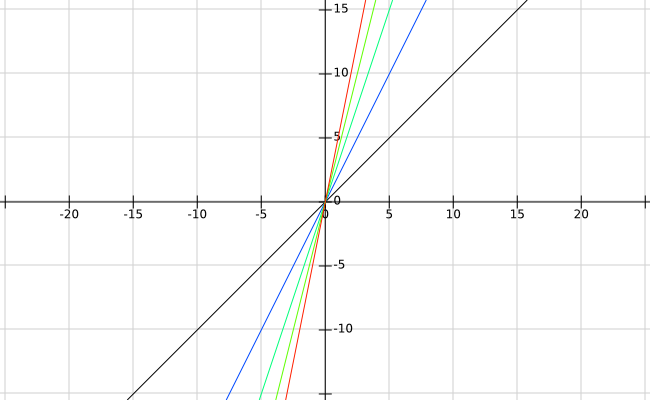
我们发现，$k$值增大使得函数更陡峭。
因此，对于一次函数，我们可以用 k 值大小来表示它的斜率。

这个定义听起来很唐突、很随意啊... 高大上的感觉顿时都没有了...

更一般地说，斜率也可以这么得出:

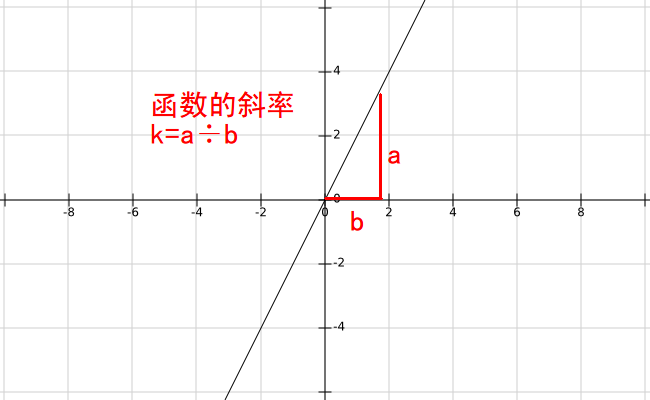
这样，我们对于斜率就有精确的定义了，它不再是一个模糊的概念，而是一个可以拿来比较大小的数值了。比方说，$y=2x$ 的斜率就是 $2$。

你可能被这些概念搞得有点懵。重新强调一遍，斜率描述一条线的陡峭程度。而一次函数的 $k$ 值越大，图像越陡，所以对于一次函数，我们可以用 $k$ 值大小来描述它的斜率。

如果你就是没办法把 $k$ 和斜率联系起来，稍微喘口气，再往下看吧。

1.1.1 [选读] 斜率的严格定义

（对于初三及以上水平的读者，可以有选择性地阅读这些标有"[选读]"文字的部分，因为这些部分可以加深对一些知识的理解。如果你不想看，跳过也没关系。

警告：数学重灾区，请在监护人的陪同下观看。）

---

先看看百度百科上的斜率词条：

slope，又称 “角系数”，是一条直线对于横坐标轴正向夹角的正切，反映直线对水平面的倾斜度。

如图，$直线P_1P_2$的斜率即为$k=tanα=\frac{y_2-y_1}{x_2-x_1}$。
其中$α$又被称为倾斜角，取值范围为$0^\circ \leq α<180^\circ$。

故：当直线的斜率存在时，斜截式 $y=kx+b$，其斜率即为 $k$。

---

1.2 点的斜率？

到现在为止，我们所讨论的函数都仅限于一次函数。你可能觉得数学家们真是一群闲得蛋疼的人，一个简单的 $k$ 值都要起个难听的名字。况且，这和微积分有个卵关系？

别猴急，我们先来进一步讨论斜率的含义。在我们搞清楚这些基本概念前，空谈微积分是没啥意义的。

---

言归正传。
对于二次函数或者反比例函数，又该如何表示它的斜率呢？

先来看看这个熟悉的二次函数吧。

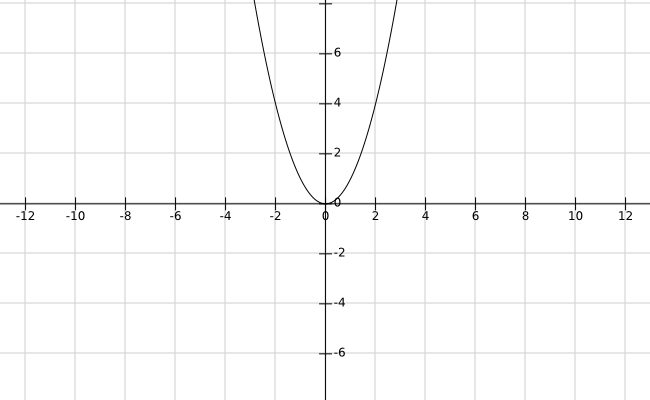
相信这样简单的U型的函数，你已经非常熟悉了。
但是，在表示它的斜率时，你会发现有点小麻烦，不，是大麻烦。

对于这个函数，我们还能用 $k$ 值来表示它的倾斜程度吗？

稍做思考，你会发现行不通。这个函数的陡峭程度不是用一个 "陡" 或者 "平" 能描述得了的。它的图像自左向右，先是快速下降，再逐渐减缓，在原点处猛地拐了一个 180 度的大弯，又开始逐渐变快、飞速上升。

那么，显然它的整个图像的斜率已经无法直接表示了。我们是不是能求出其中一段的斜率呢？

比方说，在y轴右边的这半个曲线，如果只看从0到2这一小段，你会觉得它很像$y=2x$的一小段。

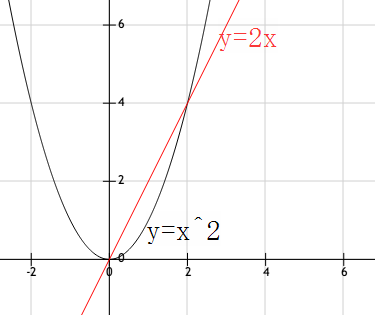
嘿，这一段的斜率是不是差不多是 $2$ 呢？

不对。

唔，也不能说是全错，毕竟只是弯了点啊。。

所以让我们继续放大图像，取更小的区间试试？
于是我们放大大大大大大大大大大大大大（此处省略N个大）

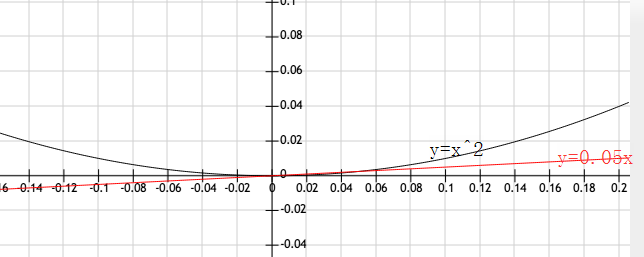
诶，这两个图像看起来有一部分重合了呢？！
也不全然，毕竟前者是曲线，后者是直线呐。。
显然，即使我们放大下去，两个图像也很难有相同的部分，或者说不可能有。
看来硬凑直线的方法行不通，得换个思路。

---

咳，如果你看得一头雾水，稍微提示一下：

我们是否能对图像上的一个点求斜率呢？

例如对于 $A (1,1)$ 这个点，我们在它的左右各取一个点 B、C，并逐渐靠近它:

PS: 从这里我开始尝试使用 GeoGebra 来作图，网页版的画图实在是太！蛋！疼！了！。。

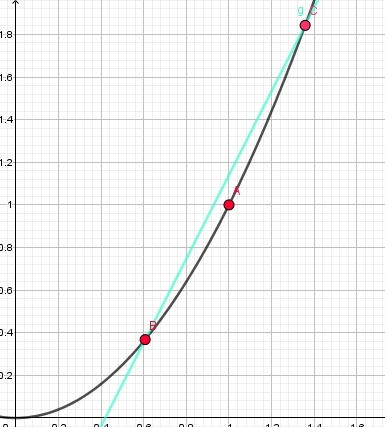
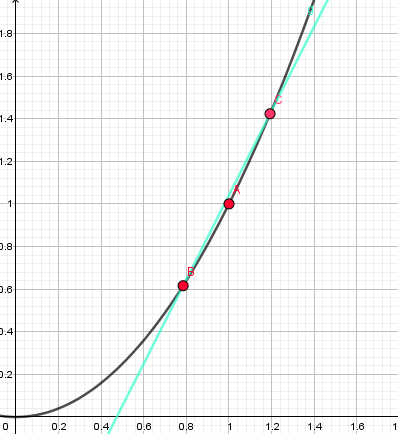
就这样不断靠近靠近。。


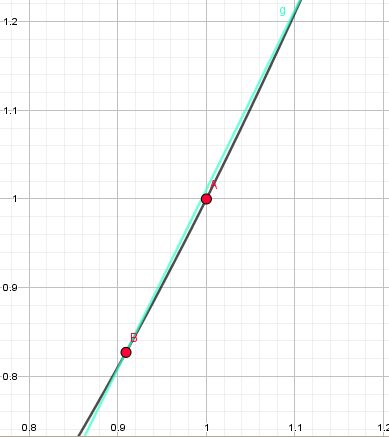
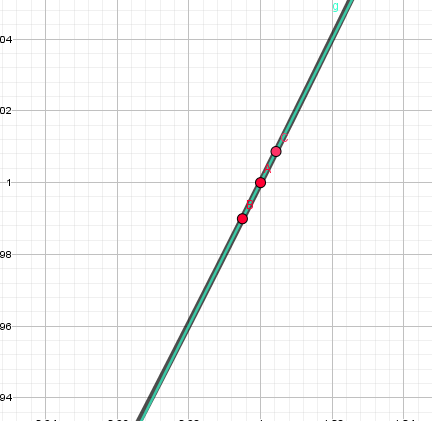
终于，在N+N次逼近A点后，三个点几乎实现了重合:

注意，我这里之所以强调几乎，是因为它们确实没有碰上，只是它们之间的距离已经微小到了无穷的小。

此时，我们仍然能作直线$BC$，我们就称这条直线为点 $A$ 在函数 $y=x^2$ 上的切线。

好了，讲了这么多，我们可以回到原来的话题了。点 A 的斜率是多少？我相信，你已经心中有数了吧。

点 A 的斜率就是点 A 在函数图像上的切线的斜率。

这句话初看有点儿像句绕口令，多看几次才能搞明白。

(假设你已经看明白了，如果没有，你就假装看懂了 :) )

OK，那么接下来，让我们正式开始导数的学... 哦不！可能还要加点料才行....

1.3 极限？

在介绍导数之前，我们还得弄懂另外一个概念:极限。
极限，顾名思义，就是到达了极点的状态。比如说，考试还有1分钟就要结束时题目还没有答完时的感觉，或者暑假开学前的晚上猛补作业时的感受。人们在遇到极限时通常都会想:"不行了!不行了!"

但是，数学中的极限也是这个意思吗？如果指"不行了""到头了"，又怎么能解决数学问题呢？
事实上，数学中的极限的含义更加积极，它有"尽可能靠近"的意思，也就是无限地靠近。
由于是数学，自然离不开数值了...所以，极限就是指一个数值尽可能地向另一个数靠近。

啥叫"尽可能地靠近"?举个例子，小明的家距离学校1000m，某天小明去上学，于是他与学校的距离变化如下:
1000m
∨
500m
∨
200m
∨
100m
∨
1m
∨
0.1m
∨
0.01m
∨
0.0000000000001m
...
∨
0.0000000000000000000000000001m
可以看到，小明与学校之间的距离越来越小，越来越靠近于0m，但是就是到达不了0m（因为他不想上学），于是我们就可以说

$$\lim_{距离 \to 0\ m}$$
突然给出这么一个数学式子，你可能会一脸蒙蔽：这是个啥？
查查英汉词典可得知: Lim 原来是 Limit 的缩写，而 Limit 就是"极限"的意思。下面的小字里的"$\to$"表示“向xxx靠近”，所以这里的意思是"让 距离 这个值给我向0m尽可能地靠近!"

上面这个式子就表示距离 无限地向 $0\ m$ 靠近 (但是就是到达不了$0\ m$!)

OKOK，理解了，那么让我们在式子上再加点花样吧!

$$\lim_{x \to a} f(x)=b$$
诶。。更晕了。。你可能会想:"这东西...现在我连符号都看不懂了!"别急，让我再给你挨个儿解释解释！

---

首先看这个$f(x)$，这里的$f$是啥意思呢？其实很简单，f是单词“function”开头第一个字母，“function”就是函数的意思，所以$f$就是指某个函数。比如说一次函数，在初中学习中我们表示成

$$y=2x$$ 想表示$x=1$时的值，我们得说 $$当x=1时,y=2$$ 但是到了高中数学以及高等数学中，因为这样写起来太麻烦了，所以同一个函数，我们表示成 $$f(x)=2x$$ 想表示$x=1$时的值，就可以简练地写成 $$f(1)=2$$ 是不是很方便？
（顺便说一句，这里不一定必须用$f$作为函数的标识，如果你喜欢，也可以写 $$我真是酷毙了(x)=2x,我真是酷毙了(1)=2$$ ）

---

回到上面的式子。$f (x)$ 就是以 x 为自变量的某个函数，在这里它到底是什么，我们不管它。
继续往下，下面的"$x \to a$"意思应该是"自变量x向a无限地靠近"。
这样，这个式子我们至少弄懂一半了，$\lim_{x \to a} f(x)$就是表示"对于$f(x)$这个函数，让$x$无限地逼近$a$"。
奇怪的是，式子的后面居然出现了等于号...小明上学时，与学校的距离也是一直在不停地变小啊...如果说是无限靠近$a$，又哪来的等于不等于呢？难道$f(x)$这么神奇，可以一边靠近，一边等于某个值吗？

这里就要提醒一下了：含有 $lim$ 的式子里，所有 "$=$" 的意思都有一点小小的变动，不再表示 "等于什么"，而是 “靠近什么”。

所以啊，上面这个式子表示 "当 $x$ 无限地靠近 $a$ 的时候，$f (x)$ 无限地靠近 $b$"。
啪啪啪！第一个奇怪的数学符号，终于是被我们弄明白了！

1.3.1 小练习

稍微弄几道关于极限的题来做做吧... 我们来找找感觉。

第一题

$$\lim_{x \to 1} x=？$$
唉...没什么难度嘛，直接把1代入进$x$算一下，结果就是$1$。

---

第二题

$$\lim_{x \to 3} x^2=？$$
稍微需要一点计算了，$3^2=3*3=9$，所以答案是$9$。

---

第三题

$$\lim_{x \to 0} (2x^2+5x+8)=？$$
似乎和第二题差不多么，只是计算有点麻烦了，列个式子算一下，$2x^2+5x+8=2*0^2+5*0+8=8$，结果是$8$。

---

第四题

你可能纳闷：这和一般的函数计算有什么区别？从哪里能体现出这个$lim$的特殊性？
来看这题：

$$\lim_{x \to 1} \frac{x^2-3x+2}{x-1}=？$$
妈呀，这题好像不能代入计算了？难道答案是$\frac2 0$吗？
不可能，分数的分母不能为0的...
那要怎么算呢？没有结果吗？
实际上，我们发现这个式子可以因式分解: $$\frac{x^2-3x+2}{x-1}=\frac{(x-2)(x-1)}{x-1}=x-2$$ 所以上面的题目就相当于 $$\lim_{x \to 1} (x-2)=？$$ 答案就是$-1$。

这里你可能会说：$x-1$既然为0了，又怎么能约分上面的分数呢？
我们需要再看一遍极限的概念：一个数值尽可能地向另一个数靠近。这里的$x-1$准确地说，应该是一个非常非常接近于0，但不是0的值，所以是可以约分的。
这里用到了因式分解的技巧，算是比较麻烦的一题，我们暂时搁下，不深入讨论了。

---

1.3.2 额外的问答时间

你可能还有一些问题.. 让我尝试解答一下。

问：为什么代入数值，求得的就是它的极限呢？有什么理论依据吗？
答：这个问题比较难以解释，需要牵扯到函数的连续性之类的。我们还是按下不表，以免影响了本文的易懂性。

问：上面说极限的格式是$\lim_{x \to a} f(x)=b$，怎么后面又写成$\lim_{x \to 1} x=1$了呢？
答：格式里给出的写法是大概的、通用的写法，实际使用中我们不会写成

$$f(x)=x,$$ $$\lim_{x \to 1} f(x)=1$$
这么麻烦，直接用$x$代替极限格式中的$f(x)$，其潜台词也就是默认$f(x)=x$了。

1.4 斜率的计算

嗯，讲完了斜率的画法和极限的概念，我们可以综合一下这两个知识，开始真正的导数之旅了。

我们来看看斜率到底是怎么算出来的。

我们仍然以这个函数图像$f(x)=x^2$为例。
如果我们设A点的坐标为$(x,f(x))$，那么C点坐标可以表示成$(x+h,f(x+h))$ (h是某个值)，这没问题吧？
那么

$$AC的斜率=\frac{C点纵坐标-A点纵坐标}{C点横坐标-A点横坐标}$$ 如果你看到这个式子感到一脸懵，那么你得重新看看这张图了:

一次函数的斜率是某两点的竖直高度差除以水平高度差。类似地，AC的斜率我们也可以这么写。
继续我们的计算： $$AC的斜率=\frac{C点纵坐标-A点纵坐标}{C点横坐标-A点横坐标}=\frac{f(x+h)-f(x)}{(x+h)-x}=\frac{f(x+h)-f(x)}{h}$$ 这样，我们就得到了两点之间的斜率公式。

再进一步想想，我们要求出的是点 A 的斜率，光有两点的斜率公式要怎么办呢？

不管三七二十一，咱们先把数值代进式子里面再说。A 点的坐标是（1,1），所以有

$$AC 的斜率 =\frac {f (1+h)-f (1)}{h}$$

这个式子看起来还是没法算啊... 让我们稍微再化简一下，可以发现 $f (1)=1^2=1，f (1+h)=(1+h)^2$。

所以这个式子还可以进一步化简：

$$AC 的斜率 =\frac {f (1+h)-f (1)}{h}=\frac {(1+h)^2-1}{h}$$

根据刚学到的完全平方公式，还可以再展开:

$$AC 的斜率 =\frac {(1+h)^2-1}{h}=\frac {h^2+2h+1-1}{h}=\frac {h^2+2h}{h}=h+2$$

这里的 $h$ 是多少呢？

刚才讲到，$h$ 表示的是 A 点与 C 点横坐标的距离。而这两点，在前面就说到是非常非常接近的，所以 $h$ 应该是一个很小很小的值。

很小很小...很接近很接近...有没有觉得这两句话有点熟悉？
。
。
。
。
。
。
。
。
。
。
。
。
。
没错！就是在 极限？ 这一节里，我们简要地讲了如何正确处理数学里很接近的值。

关键的地方来了！$h$ 既然很小，我们就可以把上式加上 $\lim$ 写成：

$$AC的斜率=\lim_{h \to 0}(h+2)$$
然后，后面这个式子的计算方式已经略熟悉啦，直接算出 $$AC的斜率=\lim_{h \to 0}(h+2)=2$$
这样，我们就终于得出了点 A (1,1) 在 $f (x)=x^2$ 上的切线 AC 的斜率，也就是点 A (1,1) 在 $f (x)=x^2$ 上的斜率。
看起来，计算一个点的斜率也没那么困难嘛！

1.4.1 小结

上面求斜率的过程可以概括成这几步：
1. 在要求斜率的点$(x,f(x))$附近找出一个与它很靠近的点$(x+h,f(x+h))$！
2. 把斜率用$\frac{C点纵坐标-A点纵坐标}{C点横坐标-A点横坐标}$表示出来！
3. 在式子前面加上$\lim_{h \to 0}$，代入进去计算斜率！

1.4.2 通式

从上面的过程中我们可以看出，求某个点的斜率有固定的步骤和方法。依照这个方法，理论上来说我们可以求出任何函数上点的斜率。
接下来让我们试着找出这样一个公式，来表示任何函数$f(x)$上任意的点$(x,f(x))$的斜率，这样，以后进行计算时就很方便了。
这个过程并不困难。让我们用$f(x)$来代替上面的$1$就可以了。

$$斜率=\lim_{h \to 0}{\frac{f(x+h)-f(x)}{(x+h)-x}}=\lim_{h \to 0}{\frac{f(x+h)-f(x)}{h}}$$

这就是任意函数在某一点的一般斜率公式。
呼，讲了这么多废话，我们总算开始步入正轨，而不是在各种概念上原地打转了。（哈哈）

记不住完整的公式也不要紧，需要用到的时候现场推导就可以了，理解这个有点复杂的式子才是关键。

1.4.3 求斜率有什么用？

我们已经基本掌握了求某一个点的斜率的方法。那么，这个东西有什么用处呢？
毕竟，如果没有实际用途的话，这样的数学工具看起来也没有什么意义啊...
在求导的用途中，最重要的也就是求某一点的切线的函数式。
因为用导数可以得出某一点的斜率，把斜率作为$k$代入$f(x)=kx+b$，很方便地能求出该点的切线方程。
实际上，在本文中我们就是用"某一点切线的斜率"来定义"某一点的斜率"的，是不？

依然以上面一节中的 $f (x)=x^2$ 和点 $A (1,1)$ 为例，我们来求一下 A 点的切线方程。

已经知道 A 点的斜率为 2 了，所以立即有

$$g (x)=2x+b$$ 是 A 点的切线方程。

又知道这个方程经过A点，故使用待定系数法：

$$g(1)=2*1+b=1$$ 解得 $$b=-1$$ 所以A点的切线方程就是 $$g(x)=2x-1$$ 这个结果对不对？画出来看看就知道有没有问题了。
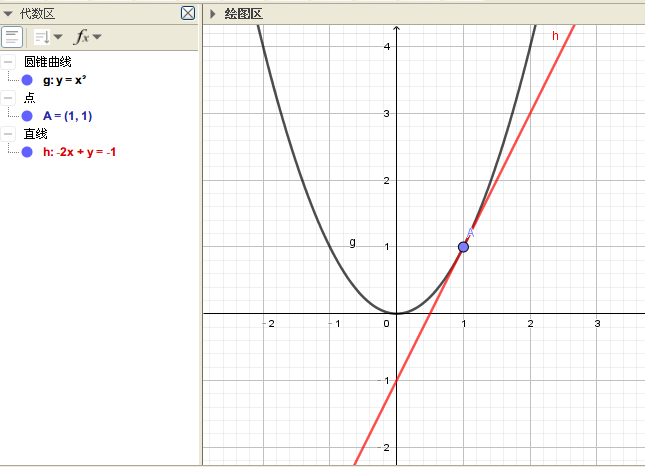
图中红色的线就是我们刚刚求出的直线。看起来它的确是A点的切线。

另一个用途是求函数的最大 / 最小值。容易看出，上面这个函数的顶点$O(0,0)$的斜率为0。
因为顶点有"这一点的前后既不在上升，也不在下降"的性质，所以顶点的斜率都应该是 0。
也就是说，只要找到一个函数中有一个斜率为0的点，就可以确定这一点是函数的一个顶点。

在接下来的 导函数 一节里，我们会讲得更多。

1.5 导函数

了解了导数和函数，这个 "导函数" 是个什么东西啊？别急，听我慢慢道来。

再看一眼这个式子：

$$\lim_{h \to 0}{\frac{f(x+h)-f(x)}{h}}$$ 其实，这个式子就是 $f (x)$ 的导函数。

函数是什么？我们复习一下函数的定义：

设 A，B 是非空的数集，如果按照某种确定的对应关系 f，使对于集合 A 中的任意一个数 x，在集合 B 中都有唯一确定的数 $y$ 和它对应，那么就称映射 $f:x\to y$ 为从集合 A 到集合 B 的一个函数，记作 $y=f (x)$。

不好意思拿错了，是这个：

在一个变化过程中，假设有两个变量 x、y，如果对于任意一个 x 都有唯一确定的一个 y 和它对应，那么就称 x 是自变量，y 是因变量，y 是 x 的函数。

也就是说，只要有一个对应关系f，就可以说f是个函数。
函是"匣子"的意思。把一个数$x$装进一个匣子，按照某个算式计算出另一个数字，就是函数。

因此，对 f (x) 求导的式子也是函数。
这个函数，对于每一个x，计算出的结果都是$(x,f(x))$在$f(x)$上的斜率。需要求导的时候，我们就不用对每个数字都重新列式求一遍了，直接代入导函数就行，很方便。

导函数一般记作 $f'(x)$。

---

继续以$f(x)=x^2$为例，我们看看它的导函数长什么样子。
这次我们不代入任何值，直接运用上面的公式：

$$f'(x)=\lim_{h \to 0}{\frac{f(x+h)-f(x)}{h}}=\lim_{h \to 0}{\frac{(x+h)^2-x^2}{h}}$$ 然后是： $$=\lim_{h \to 0}{\frac{x^2+2xh+h^2-x^2}{h}}=\lim_{h \to 0}{\frac{2xh+h^2}{h}}$$ 最后 $$=\lim_{h \to 0}(2x+h)$$
又因为h靠近0，所以直接舍去，得到： $$=\lim_{h \to 0}(2x+0)=2x$$
所以$f'(x)=2x$。

仔细观察这个式子，我们发现它很有特点。
比如说想求$A(1,1)$斜率，我们也不用重新计算了，直接用导函数就行了。

$$A的斜率=f'(1)=2$$ 同理，想求$B(2,4)$斜率的话: $$B的斜率=f'(2)=4$$ 是不是很方便？

---

导函数本身也是函数。所以对导函数$f'(x)$求导还可以得到另一个函数，称为二阶导数，一般记作$f''(x)$。
同理，还会有三阶导数$f'''(x)$、四阶导数$f''''(x)$....
当撇号过多时，比如说有个99999阶导数，直接记作$f^{(99999)}(x)$即可，不用打撇号了。

---

导函数有什么意义？只是为了装逼吗？
在了解这个问题之前，先想想导函数$f'(x)$和函数$f(x)$之间的区别和联系。

项目	$f(x)$	$f'(x)$
$x$ 对应的函数值 $y$	是函数的值	是函数 $f (x)$ 的图像上，横坐标为 $x$ 的这一点的求导结果
是否是函数	是	是
求导结果	$f'(x)$	$f''(x)$
函数零点的意义	无特殊意义	是 $f (x)$ 的顶点的横坐标

(注：零点：函数的零点就是$函数=0$这个方程的解。
比如$f(x)=x^2-1$的零点就是$x^2-1=0$的解，也就是$1和-1$ 。）

所以，导函数有一个重要的作用，就是计算函数的顶点坐标。
由于顶点的特殊性，该点的斜率是0，所以只要找出导函数$f'(x)$的零点，相当于找到了顶点。

以 $f (x)=ax^2+bx+c$ 为例。它求导的结果是 $f'(x)=2ax+b$。

$f'(x)=0$ 的解就是 $x=-\frac {b}{2a}$。这是不是与你在课堂上学到的二次函数的最值完全一致？

---

导函数的另一个作用是画函数草图。

前面已经说过，如果导函数$f'(x)>0$，说明函数在这一点上的斜率是正的，也就是说，在这一点的前后，函数应该呈上升的趋势。
相反，如果$f'(x)<0$，说明函数在这一点上的斜率是负的。在这一点的前后，函数应该呈下降的趋势。
于是乎，只要搞明白$f'(x)$的图像，就可以把$f(x)$的图像画出来了。

举个例子，如果我们要画 $f (x)=x^2+2$ 的草图，我们可以结合导函数这么画：

1. 求导，得到 $f'(x)=2x$.
2. 画出 $f'(x)=2x$ 的图像。
   
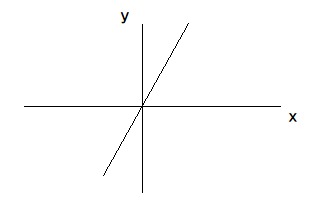
3. 准备开始画图！先找出一个起点，这里我们取 $f (0)$ 这一点，也就是 $A (0,2)$。
   
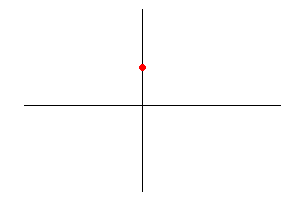
4. 按照 $f'(x)$ 的图像所示，y 轴的右边应该都是上升的，而且斜率越来越大，也就是：
   
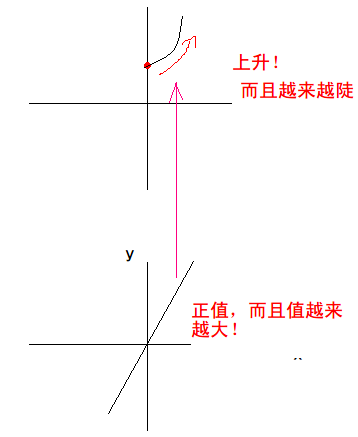
5. 同理，画出左半边：
   

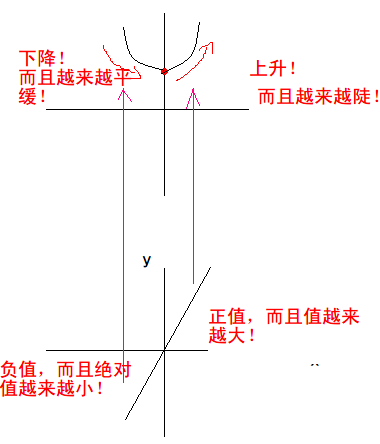
这样就把$f(x)=x^2+2$的图像大概描出来了。
这题中导函数的优势还不能充分体现出来。遇到一些比较复杂的函数，一般结合导函数这样画图比较方便。

1.5.1 导数的表示方法

前面说到，导函数一般记作$f'(x)$。
但是，实际上导函数还有一些常见的表示方法，这里介绍两种，以备后面的装逼使用。

第一种也就是刚刚讲的加撇号表示法。这种方法是在 19 世纪，一个叫 约瑟夫・路易斯・拉格朗日 的法国大叔发明的。

在他的表示法里，$y=f (x)$ 的导函数记作 $f'(x)$ 或者 $y'$。

这种表示方法非常常见，因为它写起来很容易，加个撇号只要花上你半秒钟的时间。

但是，它的弊端在于，如果有这么一个函数：

$$y=a+b$$
那么$y'$表示什么？

$a$ 和 $b$，到底谁才是自变量？谁是常量？

到底 $y'$ 表示是对 $a$ 求导，还是对 $b$ 求导？

不得而知。

要是有一种表示方法可以体现出对谁求导就好了。

这时，我们就需要第二种表示方法，也就是 戈特弗里德·威廉·莱布尼茨 ，另一个德国大叔的写法。他也是微积分的主要创始人，他生活在17世纪，比上面那位要早几百年。
对$y=f(x)$关于$x$求导可以表示成：

$$\frac{dy}{dx},\frac{d}{dx}y,\frac{df(x)}{dx},\frac{d}{dx}f(x)$$
这些式子看起来很让人头晕...
(正因如此，他的符号至今仍在大学数学中频频现身。)
这里的$d$是 Derivative(导数) 的首字母。
式子的含义是对分母上的自变量，求分子上的函数的导数。

其中，$\frac {d}{dx}$ 可以看成是一个整体，它乘以谁，就是对谁求导。
例如：

$$\frac{d}{dx}x^2=2x$$

所以，如果我们想要表示导数的导数，也就是 $f''(x)$，要怎么写呢？

就是：

$$f''(x)=\frac{d}{dx}*\frac{d}{dx}*y=\frac{d^2y}{dx^2}$$ 分子上加平方的位置看起来怪怪的。而且d似乎也不遵循乘法定律。
你可能觉得莱布尼兹的方法很麻烦，但是在后面的章节里，你会逐渐明白这样表示的优点。

1.5.2 小结 & 补充

到现在为止，我们已经学会了：

1. 斜率是什么 & 怎么算
2. 导数是什么 & 怎么求
3. 导函数是什么 & 怎么求

你可能还没有完全掌握以上内容，那也没关系！~
接下来我们会给出一些简单实用的公式，在你的学习过程中会频繁地使用它们来避免复杂的运算过程。一定要记牢！~

---

$$b'=0$$
$$x'=1$$
$$(kx)'=k$$
$$(kx+b)'=k$$
$$(ax^n)'=anx^{n-1}$$
以上就是最基础的一组导数公式，其中$a和b$的含义是任意常数。

记住了它们，即使不会推算导数也可以轻松求出初高中大部分函数的导函数！

尤其是最后一个，堪称初等函数大杀器...

举个例子，要求出 $y=2x^{999}$ 的导函数，直接用上面的公式：

$$y'=2*999*x^{999-1}=1998x^{998}$$ 是不是贼方便？

[选读] 这里还有一些为学过三角函数的同学补充的：

$$(sinx)'=cosx$$ $$(cosx)'=-sinx$$ $$(tanx)'=\frac {1}{(cosx)^2}$$

1.5.3 五年高考，三年模拟 (雾)

总觉得应该来几道题目练练手...
虽然这样有点像老师上课的模式，有悖本文的初衷，但是练习一下真的能掌握不少...
废话少说，放题过来！

。
。
。
。
。
。
。
。
1. 求出$f(x)=x^4-2x$的导函数。
2. 求出$f(x)=(x+2)^{11}$的导函数。
3. 求出$f(x)=x^{x}$的导函数。
4. 求出$f(x)=\sqrt{x}$的导函数。
5. 求出$f(x)=\sqrt[x]{x}$的导函数。
6. 求出$f(x)=\sqrt[sin(x)]{x^{cos(x)}}$的导函数。
7. 对于以上题目，你有什么感想？

---

作者的话：最近学业方面实在比较忙，先是期中考，又是统考月考周考什么的，今天刚参加全省联考.....(高二狗，体谅一下) 说好的两个月完工也没下落了：(

2021 年 9 月 24 日更新：作者回来啦！现在已经是一条大二狗了，国庆期间会重启更新～

---

1.5.4 导函数的四则运算

上面那几题已经让你晕头转向了？没关系！看完本节和下一节之后，你将可以很快地计算出它们从而去装 B！

迄今为止，我们提到的例子都是一些比较简单的函数（额，当然上面的几题除外）。
基本上函数里都只有一个$x$。形式也就是$x+1$，$x^2$这样的，大家都学过了。

但是，平时遇到的函数可没这么简单，数学考试里当然不会直接出这样的玩意儿来考你。即便刚刚学过二次函数，你也应该已经遇到$f(x)=x^2+3x+2$或者$f(x)=(x-2)^2+3$这样的函数了。这种东西要怎么求导数呢？

其实很简单！不妨回忆一下下我们上面提到过的例子：

以 $f (x)=ax^2+bx+c$ 为例。它求导的结果是 $f'(x)=2ax+b$。

（限时挑战任务！看看你能不能在 10 秒内找到这句话的出处：) ）

我们先不管结果是啥，只看每个部分。这个式子的每一部分我们都会求。$ax^2$的导数就是$2ax$，$bx$的导数就是$b$，$c$的导数……呃呃，一个常数的导数，永远是 $0$ 嘛。

所以…… 它的导数就是 $2ax+b$？看起来确实是这样。

我们不妨大胆猜测一下：求一个里面有加号的函数的导数，只要求出各个部分的导数，然后加起来就好啦！

然而事实是怎样呢？事实是…… 我们的猜测是对的。导数的加法就是可以这么拆开计算的。

写成公式的方式就是：

$$(A+B)'=A'+B'$$
（别忘了一撇「$'$」的含义哦，它是指对这个式子求导。）

那么，这是为啥呢？这个问题我们稍微往后放放。

我们先看看利用这个，能不能做出上面的题了。

第一题是$f(x)=x^4-2x$。
它的第一部分求导是$4x^3$（别忘了这个公式哟：$(ax^n)'=anx^{n-1}$）,第二部分的导数是$2$。所以结果就是$4x^3+2$。

第二题是 $f (x)=(x+2)^{11}$…… 额，这个怎么办呢？

其实只要一点一点乘开就好了！打开我们的 Maple，输入函数，点击展开：

然后按上面的方法，对每个部分求导就好了！

你可能会说：$(x+2)^{11}=(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)$，这么长的式子，考试的时候要展开不得累死我？

当然，这种暴力算法虽然不能实用，但是至少是可以算出来的。如果遇到这样的函数，展开是最差劲的选择，但起码是一种选择……起码是可以算出来的，是吧？

这种方法显然太蠢了。有没有更妙的方法来计算第二题呢？这就进入到咱们今天的重头戏：复合运算！

。
。
。

诶还没进呢（顶级拉扯）

因为标题是「四则运算」，加法已经说完了，我们来看看乘法吧。

（大家读到这里可能比较突兀，因为上面的练习里面忘了出相关的题了。偏偏这个乘法运算又很重要，还是希望大家快速过一遍！不要跳过哈，不然你待会儿会后悔的，哼哼）

什么叫乘法运算呢？举个例子：

$$f(x)=(x^3+3x+3)(x^2+2x+2)$$
这个函数怎么求导呢？有同学可能会说：加法是分开加，那我乘法也分开乘嘛！先对 $x^3+3x+3$ 求导，再对 $x^2+2x+2$ 求导，然后乘起来就好了吧？

但是，But，这样是完全错误的哦！不如再想想？先乘开自己求导一下，再找找规律？

算啦算啦，我知道你很想知道，先把正解放在这里：

$$f'(x)=(x^3+3x+3)'(x^2+2x+2)+(x^3+3x+3)(x^2+2x+2)'=(3x^2+3)(x^2+2x+2)+(x^3+3x+3)(2x+2)$$

这就是说，乘法的规则和加法完全不同，它的导数是对第一个式子求导，乘第二个；再对第二个式子求导，乘第一个。然后加起来。
写成公式的方式就是：

$$(AB)'=AB'+A'B$$
或者写得再「专业」一点：
$$(f(x)g(x))'=f'(x)g(x)+f(x)g'(x)$$
先尝试理解一下这个式子哈。
我知道你的心里肯定装满了大大的问号：凭啥这么算？你这是个啥计算方法？你这样算出来，真的是对的嘛？

很不幸的是，它确实是对的。凭什么呢？
这就有点超过知识范围了。
我一起放在下面的选读部分吧，如果你自认为可以，不妨挑战一下阅读！应该……不会需要太高的数学水平？（这个挑战就没有上面的「习题」那么坑了，哈哈！）

[选读] 加法求导公式的证明
要证明对两个函数 $f (x)$ 和 $g (x)$，可以推出 $(f (x)+g (x))'=f'(x)+g'(x)$。
先回顾公式：

$$f'(x)=\lim_{h \to 0}{\frac {f (x+h)-f (x)}{h}}$$ ，
所以写出 $(f (x)+g (x))'$ 的求导式子，然后摆弄一下式子的加法顺序： $$(f (x)+g (x))'\\=\lim_{h \to 0}{\frac {(f (x+h)+g (x+h))-(f (x)+g (x))}{h}} \\=\lim_{h \to 0}{\frac {f (x+h)+g (x+h)-f (x)-g (x)}{h}}\\=\lim_{h \to 0}{\frac {(f (x+h)-f (x))+(g (x+h)-g (x))}{h}}\\=\lim_{h \to 0}{\frac {f (x+h)-f (x)}{h}}+{\frac {g (x+h)-g (x)}{h}}\\=f'(x)+g'(x)$$
这就证完了！

---

[选读] 乘法求导公式的证明
要证明对两个函数 $f (x)$ 和 $g (x)$，可以推出 $(f (x) g (x))'=f'(x) g (x)+f (x) g'(x)$。
还是写出 $(f (x) g (x))'$ 的求导式子：

$$(f (x) g (x))'\\=\lim_{h \to 0}{\frac {f (x+h) g (x+h)-f (x) g (x)}{h}}$$
呃，这里不太好办了…… 只有两项，怎么玩它呢？
其实可以试试「凑项」！具体来说，就是加一个什么东西，再减去它，这样式子依然不会变，就像 $123+1-1$ 还是 $123$ 一样！

我们这里要凑进去的是 $f (x+h) g (x)$，详细地说就是凑成下面这样：

$$(f(x)g(x))'\\=\lim_{h \to 0}{\frac{f(x+h)g(x+h)-f(x)g(x)}{h}}\\=\lim_{h \to 0}{\frac{f(x+h)g(x+h)-f(x+h)g(x)+f(x+h)g(x)-f(x)g(x)}{h}}\\=\lim_{h \to 0}{\frac{f(x+h)(g(x+h)-g(x))+(f(x+h)-f(x))g(x)}{h}}\\=\lim_{h \to 0}{f(x+h)\frac{g(x+h)-g(x)}{h}}+\frac{f(x+h)-f(x)}{h}g(x)\\=f(x+h)g'(x)+f'(x)g(x)$$
注意，h 是无限趋近于 0 的，所以上式也就是 $f(x)g'(x)+f'(x)g(x)$ 了。

PS：这两个证明乍一看很麻烦，但是自己动手写一遍，你会发现还挺简洁的……

2021 年 11 月 21 日更新：有人问我联系方式，其实我博客里写得挺全的了：https://w568w.eu.org/about.w568w.html

2023 年 1 月 27 日更新：有关本教程的后续更新，见：https://w568w.eu.org/2023-sweep.html

2023 年 2 月 13 日更新：后续内容已更新！见：https://w568w.eu.org/calculus-1st.html