无痛的增强学习入门：泛化迭代

未分类

系列导读：《无痛的增强学习入门》系列文章旨在为大家介绍增强学习相关的入门知识，为大家后续的深入学习打下基础。其中包括增强学习的基本思想，MDP框架，几种基本的学习算法介绍，以及一些简单的实际案例。

作为机器学习中十分重要的一支，增强学习在这些年取得了十分令人惊喜的成绩，这也使得越来越多的人加入到学习增强学习的队伍当中。增强学习的知识和内容与经典监督学习、非监督学习相比并不容易，而且可解释的小例子比较少，本系列将向各位读者简单介绍其中的基本知识，并以一个小例子贯穿其中。

在第一篇中，我们以蛇棋为例，主要介绍了增强学习的核心流程，那就是Agent与Environment的交互。

无痛的增强学习入门：基本概念篇

在第二篇中，我们曾简单介绍了计算最优策略的方法——先得到同一状态下不同行动的价值估计，再根据这些价值估计计算出最优的策略选择。

无痛的增强学习入门： 增强学习形式化

在第三篇中，详细介绍了采用这个战术实现的算法——策略迭代法（Policy Iteration）。

无痛的增强学习入门：策略迭代

在前面我们介绍了策略的迭代的算法，它可以解决蛇棋的策略规划问题，帮助我们更好地完成游戏。从算法中可以看出，算法的主要时间都花费在策略评估上，对于一个简单的问题来说，这部分时间还算好，但是对于复杂的问题来说，这个步骤的时间实在有些多了。一个最直接的想法就是——我们能不能缩短这部分的时间？比方说，我们大概估计出当前策略下每个状态的价值函数就好，这样已经可以帮助我们找出最优的策略了，再做更精细的评估实际上并不必要？这就是这四篇的主角——价值迭代法的思想来源。

无痛的增强学习入门：价值迭代

5 泛化策略迭代

5.1 两个极端

在上一节我们卖了一个关子，那就是为什么价值迭代的运算速度反而不快。这一节我们将来解答这个问题。让我们回到问题，来看看前面介绍的两种算法的特点。

策略迭代法的中心是策略函数，通过策略评估+策略提升两个步骤使策略变得越来越好；价值函数通过自我更新、动态规划的方式不断迭代更新价值函数，并最终求出策略函数。我们可以看出两者的一些特点：

• 两个方法都要求策略函数和价值函数
• 最终最优的策略函数都是由价值函数得到的
• 价值函数依据函数的数值收敛
• 策略函数依据策略收敛

我们发现了一个关键：那就是两者都需要训练策略函数和价值函数，只是侧重点不同。策略迭代的核心是策略，为了使策略能够提升，价值函数可以求解得准确，也可以求解得不准确；价值迭代的核心是价值，算法的核心部分根本没有出现与策略有关的内容，直到最后才出现了策略。

两种方法都十分看重自己关心的那部分，而可以选择忽略另一部分，因此可以看出两个方法都比较极端。既然我们找到了两个极端的方法，那么我们可不可以找到两种方法的中间带呢？当然是可以的，这就是本节要介绍的泛化迭代法，英文一般称为Generalized Policy Iteration，但我觉得这个词里只出现Policy是不够准确的。

5.2 泛化迭代法

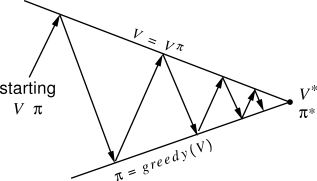
图1 泛化迭代示意图

上面图1展示了泛化迭代的一个基本形式。所谓的泛化迭代，是将解决这一类问题的算法归纳成一个算法族，并总结这一类算法的特点。图上展示了两条主线，下面一条线是策略的更新线，如果我们把策略想象成一个连续的空间，那么它就是从某套策略出发，连续地逼近最优策略-价值对。上面一条线是价值的更新线，因为我们前面遇到的问题中，价值函数是连续的，所以这条线并不难得到。

图中的折线主要表达了策略迭代的算法，我们选定某个策略，求解价值函数，然后更新策略，这样优化的轨迹会不断地在两条主线上跳动。而对于价值迭代的算法，则是一直在上面那条线上行走，如图2所示：

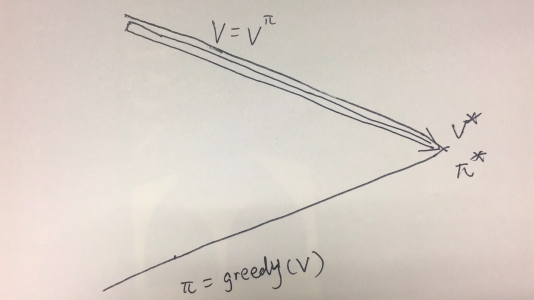
图2 价值迭代法的示意图

那么还有别的优化方法么？前面提到我们已知的两种方法是两个极端，它们就像一条线段的两个端点一样，其他的算法都可以由这两个方法加权平均得到，比方说下面这个算法，如图3所示：

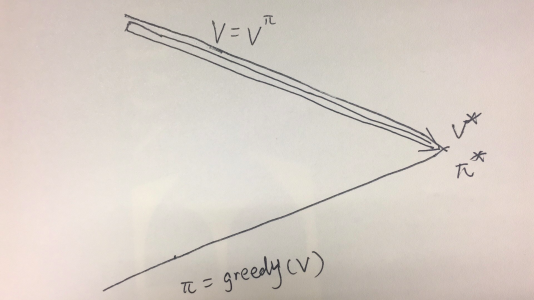
图3 泛化迭代的示意图

我们先做几轮价值迭代，然后再做策略迭代，这样的方法同样可以得到正确的结果，但是可能会有更快的速度。

那么我们回到上一节的问题中，为什么价值迭代的方法会慢？

由于我们的蛇棋问题是一个离散的状态，对应的策略也是离散的，因此这个问题的示意图是这样的：

图4 蛇棋问题的泛化迭代图

由于策略是离散的，所以任意一个策略可能和某个范围内的价值函数对应，因此在价值函数优化到某一步时，已经可以得到最优的策略，然而按照价值函数算法的定义，我们要等到价值函数在数值上收敛。而随着优化过程不断进行，最后的优化将会变得比较艰难，因此这个算法需要的时间比较长。

5.3 实现

通过上面的分析，我们就可以尝试将两种算法结合起来。

def generalized_policy_iteration(self):
    self.value_iteration(10)
    self.policy_iteration(-1,1)

这个函数就是泛化优化的一种实现形式，它的算法是先执行10轮价值迭代的优化，然后进行策略迭代，同时策略迭代中的策略评估只进行一个循环的更新。经过这样的设计，我们可以看看它的用时：

np.random.seed(0)
    env = Snake(10, [3,6])
    agent = TableAgent(env.state_transition_table(), env.reward_table())
    with timer('Timer PolicyIter'):
        agent.policy_iteration()
    print 'return_pi={}'.format(eval(env,agent))
    print agent.policy
    print '================='
    agent2 = TableAgent(env.state_transition_table(), env.reward_table())
    with timer('Timer ValueIter'):
        agent2.value_iteration()
    print 'return_pi={}'.format(eval(env,agent2))
    print agent2.policy
    print '================='
    agent3 = TableAgent(env.state_transition_table(), env.reward_table())
    with timer('Timer GeneralizedIter'):
        agent3.generalized_policy_iteration()
    print 'return_pi={}'.format(eval(env,agent3))
    print agent3.policy

从代码中可以看出，我们同时进行了3组实验，分别是策略迭代，价值迭代和我们给出的一种泛化迭代法，那么它们的结果如何呢？

Timer PolicyIter COST:0.186598777771
return_pi=84
=================
Timer ValueIter COST:0.0881521701813
return_pi=84
=================
Timer GeneralizedIter COST:0.0130021572113
return_pi=84

虽然实验比较粗糙，但是我们还是可以明显看出几个算法在时间上的差距。通过一定的设计，泛化迭代确实可以做到更快的计算和收敛。当然，泛化迭代带给我们的不止是更快的速度了。

5.4 从模型已知到无模型算法

前面我们接触过的问题有一个特点，那就是我们可以看到蛇棋的棋盘，换句话说，我们可以了解到整个游戏的全貌，当我们发现前方有一个梯子时，我们可以根据前方是上升梯子还是下降梯子来决定使用哪个骰子，或者使用遥控骰子。这时候我们相当于站在了上帝视角，能够看清一切情况。

但一个可悲的事实是，在很多实际问题中，我们无法得到游戏的全貌。这其中有几个原因，一是游戏的全貌可能十分复杂，复杂到我们难以把所有的状态罗列出来。比方说围棋问题，每一个格子上都可以有三个状态：无子，黑子和白子，那么19*19=361个格子，我们一共有$3^{361}$个状态，这样数量的状态想要罗列清楚是十分困难的。另一种是中间的一些状态过渡的信息无法获得，比方说我们下面的进阶版蛇棋，在这个新版蛇棋中，我们将不再显示棋盘和骰子的投掷数目，每一次当玩家选择完所使用的手法后，玩家将直接得到棋子的下一个落脚点。也就是说：

这个公式将不再变得已知了。对于这样的盲棋，我们该如何解决？前面的学习算法很优雅，但是需要太多的环境信息，此时当我们去掉了这些信息，我们需要换个思路。而这个思路，才是增强学习的精髓。

增强学习的一大特点是才尝试中不断学习。在前面的问题中，我们的Agent并没有进行尝试，就可以直接完成学习的任务，Agent仿佛是一个战略指挥家，等到一切局势确定，开始战略部署。而现在，眼前的问题充满了迷雾，指挥家也不得不放下身段，亲自参与其中，通过尝试获得最优策略的经验。

那么新的算法的思路大致如下所示：

1. 确定一个初始算法（这和前面的算法一致）
2. 用这个算法进行游戏，得到一些游戏序列（episode）：${s1,a1,s2,a2,…,s_n,a_n}$
3. 一旦游戏的轮数达到一定数目，我们就可以认为这些游戏序列可以帮助我们对环境模型做一定的归纳总结。那么我们就可以对当前策略进行评估，得到对应的价值函数
4. 得到了价值函数，就可以重新进行策略改进了，这时候我们又回到了前面算法的路子上来。

接下来我们要接触两个算法：分别是蒙特卡罗法和策略迭代法。关于它们的内容我们下一节再说。

作者介绍：冯超，毕业于中国科学院大学，猿辅导研究团队视觉研究负责人，小猿搜题拍照搜题负责人之一。2017年独立撰写《深度学习轻松学：核心算法与视觉实践》一书（书籍链接：https://item.jd.com/12106435.html），以轻松幽默的语言深入详细地介绍了深度学习的基本结构，模型优化和参数设置细节，视觉领域应用等内容。自2016年起在知乎开设了自己的专栏：《无痛的机器学习》，发表机器学习与深度学习相关文章，收到了不错的反响，并被多家媒体转载。曾多次参与社区技术分享活动。