机器视觉Note1(线性分类器)

算法

---

---

在图像分类任务中，我们希望将一张图片映射到一个文本标签上，如上图所示。当我们给计算机读入一张照片，我们希望计算机告诉我们这张照片所描述的内容。

下面尝试构造一个线性分类器，来实现对图片分类。每张图片有 $D$ 个pixel，每个像素的范围在0-255，将图像像素矩阵压成一维构成一个 $D$ 维的行向量，我们有 $K$ 个类别，很自然的想到可以将这 $K$ 个类别也用 $K$ 维的行向量表示，每一个位置代表一种类别。现在图片的分类问题很自然的转换为构造一个函数，$f : R^D \rightarrow R^K$，这函数原始图像像素到分类分值的映射。

本例子使用最简单的线性映射：

$$f(x_i,W,b) = Wx_i + b$$
这个矩阵 $W$ 是一个 $K * D$ 的矩阵 ，矩阵 $W$ 乘以 图像向量$x_i$ 加上篇置项 $b$，将输出10个数字，表示这张图片的标签应该是哪类。下面的图片很好的解释这个映射的作用。下图中得到的结果向量，dog 位置得到了更高的分数，但是图片明显是一张猫，在后面我们会通过损失函数构建权重与正确分类的关系，更正 $W$ 的权重系数。

---

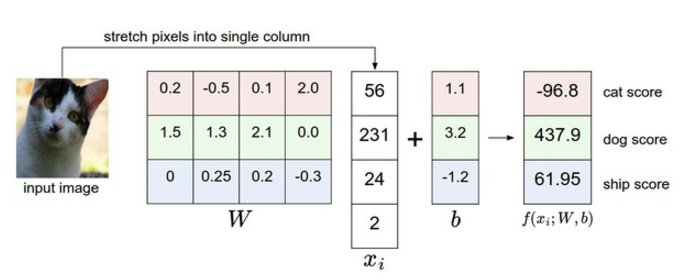
理解线性分类器

关于权重矩阵我们可以从两个角度去理解每一个权重矩阵中行向量所代表的意义：

• 将图像看做高维的点，每个权重行向量可以看做高维的一个平面，对图像分类就相当于，将不同类别的图片高维的点用这些权重向量构成的平面进行分割，在该平面上面并且离该平面越远，则更加确信为该类别。下面的图是将高维度数据降至二维可视化后的结果。

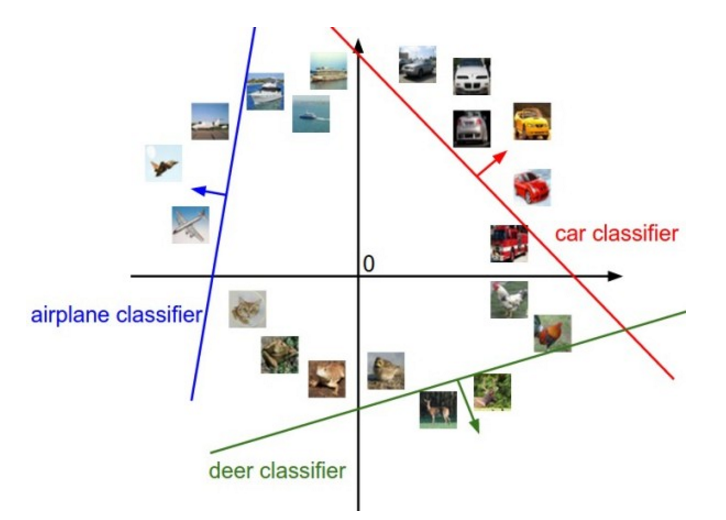
• 另一种权重的解释是，权重矩阵的没一行代表一个分类的模板，通过内积来比较图像和模板，将最相似的图片分至模板所代表的类别。下图是将训练后所获得的权重矩阵W的每一行可视化后，获得的模板。可以看出每一个模板与该类别图片的关系。例如plan的背景大多为蓝色，所以模板也以蓝色为主.
  

  内积公式 : $ab = |a||b|cos(\theta)$
  当向量间夹角越小，内积值越大。当夹角为90°，内积值为0

---

偏差和权重的合并技巧

$f(x_i,W,b) = Wx_i + b$
分开处理这两个参数（权重参数 $W$ 和偏差参数 $b$）有点笨拙，一般常用方法是把两个参数放到同一个矩阵中，将向量$x_i$向量增加一个维度，这个维度的数值是常量1，同时 $W$ 权重增加一个维度，这个维度就是向量 $b$,这样我们只需要学习一个权重矩阵，而不用去分别权重矩阵和偏差的矩阵。

---

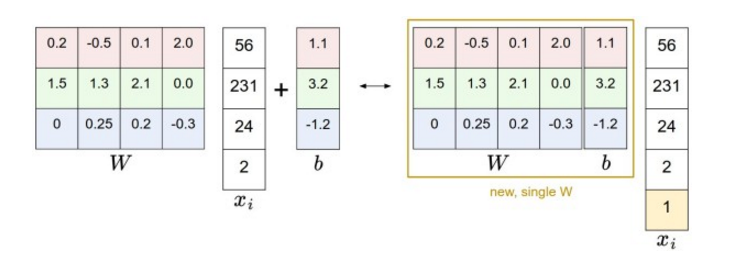
损失函数Loss function

Multiclass Support Vector Machine Loss
损失函数的具体形式有很多，在这里我们使用SVM损失函数，该损失函数的目标是正确分类上的得分始终比不正确分类上的得分高出一个边界值 $\bigtriangleup$。
针对第$j$个类别的得分公式 : $s_j = f(x_i,w_j)$。
那么，第 $i$ 个数据的多类损失函数可以写成以下形式:

$L_i = \sum_{j\neq y_i}\max(0,s_j - s_{y_i} + \bigtriangleup)$

举例 : 假设有3个分类，并且得到了分值 $s = [13,-7,11]$。其中第一个类别是正确的类别，同时假设 $\bigtriangleup$ 是10，上面的公式是将所有不正确的分类($j \neq y_i$)加起来，所以我们依照公式计算损失函数的过程可以写成如下计算过程:

$L_i = \max(0,-7 - 13 + 10) + \max(0,11 - 13 + 10)$

理解了以上计算过程，我们可以将损失函数改写成以下形式:

$L_i = \sum_{j\neq y_i}\max(0,w_jx_i - w_{y_i}x_i + \bigtriangleup)$

$\max(0,-)$函数被称为折页损失(hinge loss) 。
$\max(0,-)^2$函数被称为平方折页损失(L2-SVM) 。 平方折页损失更强烈的惩罚过界的边界值。

多类SVM“想要”正确类别的分类分数比其他不正确分类类别的分数要高，而且至少高出delta的边界值。如果其他分类分数进入了红色的区域，甚至更高，那么就开始计算损失。如果没有这些情况，损失值为0。我们的目标是找到一些权重，它们既能够让训练集中的数据样例满足这些限制，也能让总的损失值尽可能地低。

其它SVM公式 ，除了本文使用的SVM公式。另一种常用的是One-Vs-All (OVA) SVM , 还有一种使用较少的叫做 All-VS-ALL(AVA)，本文构造的损失函数SVM性能优于OVA。

SoftMax
SoftMax分类器可以理解为逻辑回归分类器面对多分类问题的一般归纳，Softmax输出的是归一化的分类概率，更加直观，并且从概率上可以解释。
SoftMax的输出函数如下，其输入值是一个向量，其值在0-1范围内，相当于归一化后的结果:

$f_i(w_ix_i) = \frac{e^{w_ix_i}}{\sum\limits_{k}e^(w_k*x_i)}$

SoftMax的损失函数定义如下,其中 $y_i$ 是对应第 $i$ 条数据的目标输出结果，$f(wx_i)$ 是当前输出结果:

$L_i = (1 - y_i)log(1-f(wx_i)) + y_ilog(f(wx_i))$

信息轮中将“真实”分布 $p$ 和估计分布 $q$ 之间的交叉（Relative Entropy）熵定义如下:

$H(p,q) = -\sum\limits_{x}p(x)log(q(x))$

而softmax的分类器的输出结果就相当于估计分类概率，相当于 $q(x)$ 而 计算所得的 $L_i$ 可以看做真实分布与估计分布的交叉熵，值越小，表明真实分布与估计分布越近似。也就是交叉熵损失函数'期望'预测分布的概率密度都在正确分类熵。

数值稳定:
编程实现Softmax函数计算时，中间项存在指数函数，所以数值可能非常大，除以大数值可能导致数值计算的不稳定，所以在编程计算过程中使用归一化技巧非常重要。如果在分母中都乘以一个常数C，并把它变换到求和之中，会得到一个等价的数学公式:

$$\frac{e^{f_{y_i}}}{\sum_je^{f_j}} = \frac{e^{f_{y_i} + logC}}{\sum_je^{f_j + logC}}$$
其中 $C$ 的值可以自由选择，通过这个技巧可以提高计算中的数值稳定性。通常我们将 $C$ 设为 $logC = -\max(f_j)$,该技巧简单的说，就是通过数值平移，使指数函数的值缩小。

损失函数可视化
损失函数通常都会定义在一个高纬度空间中(权重矩阵 $w$ 所处的空间属于高维空间)，这样很难，通常很难对数据进行可视化，然而仍可以采用在1个维度($w + xw_1$)的方向或者2个维度($w + xw_1 + yw_2$ )的方向上对高维进行切片，这样可以获得一些直观的感受。

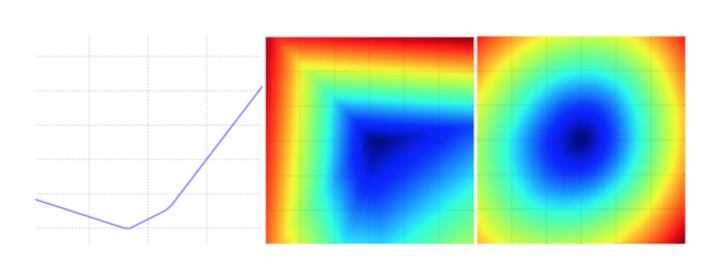
一个无正则化的多类SVM的损失函数的图示。左边和中间只有一个样本数据，右边是CIFAR-10中的100个数据。左：a值变化在某个维度方向上对应的的损失值变化。中和右：两个维度方向上的损失值切片图，蓝色部分是低损失值区域，红色部分是高损失值区域。注意损失函数的分段线性结构。多个样本的损失值是总体的平均值，所以右边的碗状结构是很多的分段线性结构的平均（比如中间这个就是其中之一）

---

正则化 Regularization

如果我们像上面一样设计损失函数会出现一个问题，假如我们找到了一个权重 $W$ 能够正确地分类每个数据(即所有的边界都满足，并且对于所有的 $i$ 都有 $L_i = 0$)。然而这个权重 $W$ 并不唯一，假如将 $W$ 乘以一个大于 1 的 系数 $\lambda$ 任何 $\lambda W$都能使损失值维0，因为这个变化将所有得分值以 $\lambda$ 大小均等的扩大了，所以每个得分之间的差距也扩大了 。

我们希望能对 $W$ 添加一些偏好，以此来消除模糊性。方法是在损失函数中添加一个正则惩罚(regularization penalty) $R(W)$部分。最常用的正则惩罚是$L2$范式，和$L1$范式。

$L1范式 \Rightarrow R(W) = \sum\limits_{k}\sum\limits_{l}w_{k,l}$

$L2范式 \Rightarrow R(W) = \sum\limits_{k}\sum\limits_{l}w_{k,l}^2$

添加正则后的SVM损失函数可以写成如下的形式，它由两个部分组成，所有样例的平均损失$L_i$，以及正则化损失。

$L = \frac{1}{N}\sum\limits_{i}L_i + \lambda R(W)$

将其改写成带入权重系数后的完整的基于L2惩罚公式为:

$L = \frac{1}{N}\sum\limits_{i}\sum\limits_{j\neq y_i}[\max(0,f(x_i;W)_j - f(X_i;W)_{y_i} + \bigtriangleup)] + \lambda\sum\limits_{k}\sum\limits_{l}W_{k,l}^2$

引入正则化，会带来很多好的性质，其中最好的性质就是对大数值权重进行惩罚，可以提升其泛化能力,例如输入向量 $x = [1,1,1,1]$,两个权重向量$w_1 = [1,0,0,0]$,$w_2 = [0.25,0.25,0.25,0.25]$ 。 虽然$w_1^Tx = w_2^Tx = 1$,两个权重都得到相同的内积，但是 $w_1$的惩罚是1.0，$w_2$的惩罚是0.25，根据惩来看$w_2$更优，L2惩罚更趋向于选择更分散的权重向量，这样鼓励分类器最终将所有维度的特征都利用起来，而不是强烈的依赖其中几个少数的维度，这一效果也会提高分类器的泛化能力，避免过拟合。

在正则化过程中我们通过引入 $\lambda$ 来控制正则项 和 svm损失之间的关系。

---

最优化(Optimization)

通过损失函数，我们建立了权重矩阵 $W$ 质量和 损失函数 $L$ 的关系，而最优化的目标就是找到对应最小损失函数值所对应的权重矩阵 $W$，对于SVM(损失函数)是一个凸优化问题，而面对非凸的函数(神经网络)，我们需要一些更加广泛的最优化技巧。

随机搜索:
就随机尝试 $W$ 权重矩阵，然后比较那个权重会获得更小的损失值，然后选择随机搜索中最优的权重矩阵 $W$ 然后去跑测试集。显然这是一个靠运气的方法，而且随着搜索空间的增大，寻找最优解需要的迭代时间越长。

bestloss = float("inf")
for num in range(1000):
    w = np.random.randn(10,3073) 8 0.0001
    loss = L(x_train,y_train, w)
    if loss < bestloss:
        bestloss = loss
        bestw = w

随机本地搜索:
第一个策略可以看做没走一步都尝试几个随机方向，如果某个方向是向下的，就向该方向走一部，而本地搜索的策略我们每次生成一个随机扰动的 $w_{random}$，而如果这个方向可以降低损失，我们就朝这个方向走，这个过程中，我们可以记忆以前所走的路径。

W = np.random.randn(10, 3073) * 0.001 
bestloss = float("inf")
for i in xrange(1000):
  step_size = 0.0001
  Wtry = W + np.random.randn(10, 3073) * step_size
  loss = L(x_train y_train, Wtry)
  if loss < bestloss:
    W = Wtry
    bestloss = loss

梯度下降：
前面的策略中，我们都是随机寻找可以降低损失函数的权重矩阵 $W$ 的方向，然而数学中，我们可以通过损失函数的梯度，找到下降的正确方向，这样时间比随机搜索快的多。

一维函数的求导公式，对于多维我们使用偏导数对梯度进行计算:

$\frac{df(x)}{dx} = \lim\limits_{h \to 0}\frac{f(x + h)-f(x)}{h}$

计算梯度有两种方法: 一个是缓慢的近似方法(数值梯度法)，但实现简单。另一种方法是(分析梯度法)计算迅速，结果精确，但是实现时容易出错，并且需要微分。

数值梯度法:

@ f 函数，接受权重 w
@ x 权重矩阵 w
def eval_num_gradient(f,x):
    fx = f(x)
    grad = np.zeros(x.shape)
    h = 0.00001
    # 对x中所有的索引进行迭代
    it = np.nditer(x, flags = ['multi_index'], op_flags = ['readwrite'])
    while not it.finished:
        # 计算 x + h 处的函数值
        ix = it.multi_index
        old_value = x[ix]
        x[ix] = old_value + h
        fxh = f(x)
        x[ix] = old_value
        # 计算偏导数
        grad[ix] = (fxh - fx) / h
        # 计算下个维度
        it.iternext()
    return grad

在数学公式中，h的取值是区域0的，然而在实际中，用一个非常小的数值(列如1e-5)就足够了。在不产生数值计算出错的前提下，可以使用尽可能小的h，在实际计算中，利用中心差值公式(centered difference formula) $|\frac{f(x + h) - f(x - h)}{2h}|$ 效果更理想。

效率问题:
数值梯度的复杂性和参数的量线性相关。损失函数每走一步就需要计算 $m \times n$次损失函数的梯度。面对复杂的神经网络，这个问题会非常严峻。显然这个策略不适合大规模的数据，我们需要更好计算策略

微分分析计算梯度
使用微分进行分析，获得计算梯度的公式(非近似)，用公式计算速度很快，但是编程实现过程中容易出错，在实际过程中，可以通过与数值梯度法的结果进行比较，以此来检查其实现的正确性，这个步骤叫做梯度检查。

我们以SVM的损失函数在某个数据点的计算举例:

$L_i = \sum\limits_{j\neq y_i}[\max(0,w_jx_i - w_{y_i}x_i + \bigtriangleup)]$

对其求$w_{y_i}$求微分可以得到以下公式:

$$\frac{\partial L_i}{\partial w_{y_i}} = -(\sum\limits_{j\neq y_{i}}1(w_jx_i - w_{y_i}x_i + \bigtriangleup > 0 ))x_i\\ \frac{\partial L_i}{\partial w_{j}} = 1(w_jx_i - w_{y_i}x_i + \bigtriangleup > 0 )x_i$$
其中1代表示性函数 $1(condition)$ , 如果括号中的条件为真，那么函数值为1，如果条件为假，函数值维0。并且也很容易理解，对于向量乘法 $wx = |w||x|cos(\theta)$ 如果我们希望获得的值更大，我们可以将向量 $w$ 向 $x$向量的方向更新。夹角小，值越大。

小批量数据梯度下降(Mini-batch gradient descent):
在大规模的实际应用中，训练数据通常可以达到百万量集。如果每次训练整个训练集，来获得一次参数的更新就太浪费了。一个常用的方法是计算训练集中的小批量(batches)数据，来获得权重更新。基于小批量的数据梯度下降可以实现快速收敛，以此进行更加频繁的参数更新

随机梯度下降(Stochastic Gradient Descent)
下批量数据策略有个极端情况，那就是每个批量中只有一个数据样本，这种策略就被称为随机梯度下降。这种策略在实际中比较少见，因为向量化的计算，更加高效。