决策树

算法

---

1. 模型的特性

优点

1. 容易理解和解释，并且生成的决策树可被可视化。
2. 不需要特别的数据预处理(必须处理缺失值)。通常其余模型需要将数据进行标准化，哑变量，变量筛选，等等的数据预处理过程。
3. 算法的复杂度是对数级别。
4. 能够处理连续性以及离散型变量。
5. 可以处理多分类问题。
6. 可以使用统计方法对模型进行评估。

缺点

1. 决策树很容易产生严重的过拟合问题
2. 对数据变化敏感，小量的数据变化可能导致完全不同的决策树生成
3. 选择最优决策树是一个NP完全问题。只能找到局部最优解。
4. 不可以处理异或问题。
5. 数据样本的不平衡，可能会导致错误的决策树被建立。

2. 属性选择

信息增益(Information gain)

信息增益基于香浓的信息论，它基于分裂前后的信息差异选择分裂属性,找出信息增益值最大的属性，作为分裂节点。节点所包含的信息计量(熵)的定义如下：

$$Info(D) = -\sum_{i=1}^mp_ilog_2(p_i)$$
其中 $m$ 表示数据集 $D$ 中类别 $C$ 的个数，$pi$ 表示 $D$ 中任意一个类别 $C_i$ 的概率($p_i=\frac{count(C_i)}{count(D)}$). $Info(D)$ 表示数据集D在此种概率分布下，不确定性的大小.

信息增益所表示的是当我们引入一个新的变量时，元数据在新的概率分布下不确定性的变化。可以看出随着概率分布更加均衡，以及数据集中分类可能性的增多，熵的值越大，不确定性也更高

信息增益表示，数据集在某个属性节点分裂前后分布不确定性的变化。

$$Gain(R) = Info(D) - Info_R(D)$$
分裂后的熵计算公式如下:
$$Info_R(D) = -\sum_{j=1}^{k}\frac{|D_j|}{|D|}\times Info(D_j)$$
上述公式中 $Info_R(D)$表示使用 $R$ 节点分裂后新形成的数据集的熵，$R$ 有 k 个不同的取值$\lbrace V_1,V_2 ,\ldots,V_k\rbrace$,于是可以将 $D$ 根据 $R$ 的取值分成 k 组 $\lbrace D_1,D_2,\ldots,D_k \rbrace$
信息增益$Gain(R)$表示属性R节点使分类分布不确定性的变化，我们寻找$Gain$最大的属性，就能使分类后的结果更纯，最可能把不同的类别分开。ID3算法就是基于信息增益来进行属性的选择。

增益比率(Gain ratio)

基于信息增益进行属性选择有一个很大的缺陷，它会倾向于选择属性值多的属性。一个较为极端的例子是某种属性将预测属性完全分割，也就是在该属性分割后预测属性在每个分割集中，只有一种可能，分割后的预测属性的不确定性很小。但这样的分割方式往往没有任何意义，缺乏泛化能力。

信息增益比率对上面的情况进行了改进，它引入了一个分裂信息：

$$SplitInfo_R(D)=-\sum_{j=1}^{k}\frac{|D_j|}{D}\times log_2(\frac{|D_j|}{|D|})$$
增益比率定义为信息增益与分裂信息的比值：
$$GainRatio(R)=\frac{Gain(R)}{SplitInfo_R(D)}$$
可以选择$GainRatio(R)$最大的属性为最佳的分裂属性。C3算法采用此方法选择分裂节点。

$GainRatio(R)$通过$SplitInfo_R(D)$对属性较多的节点进行惩罚，如果一个节点的属性取值很多，那么$SplitInfo$会增大，使$GainRatio$变小，不过当一个节点属性很少也可能会导致$SplitInfo$取值为0或者趋于0，使$GainRatio(R)$的值变得不可信，可以通过引入平滑系数对信息增益比率进行改进。

$$GainRatio(R)=\frac{Gain(R)}{\overline{SplitInfo(D)}+SplitInfo_R(D)}$$

基尼指数(Gini index)

基尼指数是另外一种数据的不纯度的度量方法，定义如下：

$$Gini(D) = 1 - \sum_{i=1}^{m}P_i^2$$
其中$m$仍然表示数据集D中类别C的个数，$P_i$表示D中任意一个记录属于$C_i$的概率，计算时$P_i=\frac{counts(C_i)}{counts(D)}$.如果所有的记录都同属于一个类别中，则$P_1=1$,$Gini(D)=0$，此时不纯度最低。算法CART(Classification and Regression Tree)算法中利用基尼指数构造二叉决策树。
$$Gini_R(D)=\frac{|D_1|}{|D|}Gini(D_1) + \frac{|D_2|}{|D|}Gini(D_2)$$
其中$D_1$为$D$的一个非空真子集，$D_2$为$D_1$在$D$的补集，对于某个属性，可能有很多个真子集，我们选择最小的值作为属性R的基尼指数。
$$\Delta Gini(R)=Gini(D)-Gini_R(D)$$
我们将$\Delta Gini(R)$值最大的属性最为最佳的分裂节点。

3. 剪枝

在决策树学习中将已经生成的树进行简化的过程称为剪枝。具体的说就是从已生成的树上裁剪掉一些子树或叶结点，并将其根节点或父结点作为新的叶结点，从而简化分类树模型，减轻过拟合问题。

决策树的剪枝往往通过极小化决策树整体的代价函数(cost function)来实现，代价函数如下:

$$C_\alpha(T)=\sum_{t=1}^{|T|}N_tH_t(T) + \alpha|T|$$
其中树T的叶结点个数为$|T|$,t是树T的叶结点，该叶结点有$N_t$个样本点，其中k类的样本点有$N_{tk}$个，$k=1,2,\cdots,K$ , $H_t(T)$为叶结点的t上的熵，$\alpha \geq 0$为参数。
$H_t(T)$的公式为:
$$H_t(T)=-\sum_{k}^{K}\frac{N_{tk}}{N_t}log\frac{N_tk}{N_t}$$
可以将损失函数函数改写为:
$$C_\alpha(T)=C(T)+\alpha|T|$$
其中$C(T)$表示模型对训练数据的预测误差，即模型与训练数据的拟合度，$|T|$表示模型复杂度,参数$\alpha$控制两者之间的影响，较大的$\alpha$倾向于选择较为简单的模型，较小的$\alpha$倾向于选择较为复杂的模型。式中定义的损失函数的极小化等价于正则化的极大似然估计。所以剪枝等价于利用正则化的极大似然估计进行模型选择。
剪枝的流程如下：

1. 计算每个节点的熵。
2. 递归的从树的叶结点向上回缩。设一组叶结点回缩到其父节点之前与之后的的整体分别为$T_A$与$T_B$，其对应的损失函数分别是$C_\alpha(T_A)$与$C_\alpha(T_B)$,如果:
   $$C_\alpha(T_A) \geq C_\alpha(T_B)$$ ,那么进行剪枝，将子节点中最多的类作为父节点的标识。
3. 返回(2)直至该过程不能继续，得到损失函数最小的子树。

4. 算法(ID3,C4.5,CART)

ID3算法使用信息增益选择决策树分裂属性，C4.5算法使用信息增益率选择决策树分裂属性，CART算法使用基尼指数选择决策树的分裂属性。下面以CART算法介绍整个树生成以及剪枝流程：
CART是一种分类回归模型，由Breiman等人在1984年提出。可以用作分类以及回归。CART假设决策树为二叉树。

• 决策树生成
  
  1. 设结点的训练数据集为D，计算现有特征对该数据集的基尼指数。
  2. 在所有可能的特征A以及他们所有的可能的切分点$\alpha$中，选择基尼指数最优的特征以及最优切分点，依据此最优特征以及最优切分点，将训练数据集特征分配到两个子节点中。
  3. 对两个子节点递归的调用(1)(2)，直至满足停止条件。
• 决策树的剪枝
  
  1. 设$k=0$ , $T=T_0$($T_0$表示生成起始决策树).
  2. 设$\alpha=+\infty$
  3. 自下向上计各个内部节点t计算$C(T_t)$ , $|T_t|$以及
     $$g(t) = \frac{C(t)-C(T_t)}{|T_t|-1}$$
     $$\alpha = min(\alpha,g(t))$$
  4. 自上而下地访问内部节点t, 如果有$g(t)=\alpha$, 进行剪枝, 并对叶结点t以多数表决法决定其类，得到树T.
  5. $k = k + 1$ , $\alpha_k = \alpha$ , $T_k = T$
  6. 如果T不是由根节点单独构成的树，则回到步骤(4)
  7. 采用交叉验证法，在子书序列$T_0,T_1,\cdots,T_n$中选取最优子树$T_\alpha$

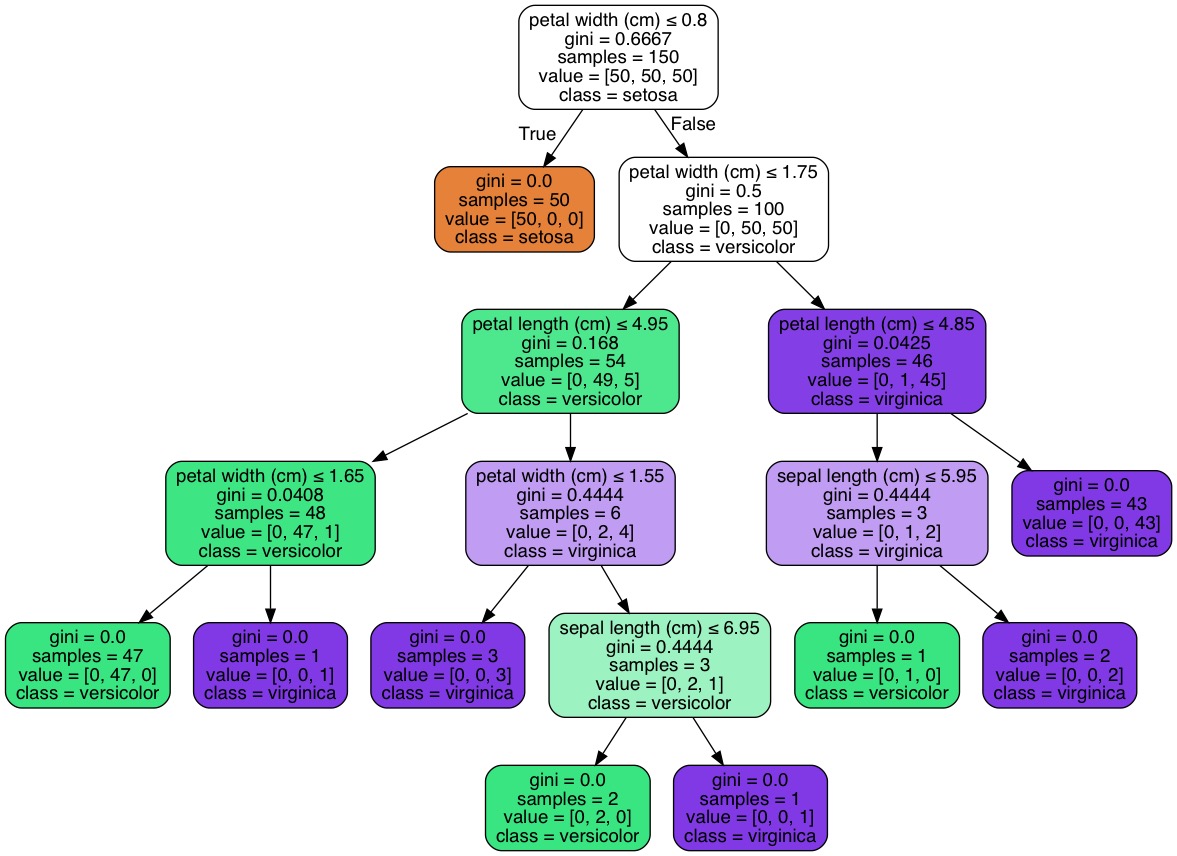
5. Python代码示例

from sklearn import tree
from sklearn.datasets import load_iris
iris = load_iris()
clf = tree.DecisionTreeClassifier()
clf = clf.fit(iris.data, iris.target)

from IPython.display import Image
import pydotplus 

dot_data = tree.export_graphviz(clf ,
            out_file=None,feature_names=iris.feature_names,
            class_names=iris.target_names, filled = True,
            rounded = True, special_characters = True)

graph = pydotplus.graph_from_dot_data(dot_data)

Image(graph.create_jpg())