贪心算法(一)

【输入】：一个或者两个集合S，T
【输出】：$max(\sum_{i\in S}f(i))$ 或者 $min(\sum_{i\in S}f(i))$

【贪心算法】目的是，能够找到某种“顺序”和“规律”，是的对集合S【一遍】扫描就可以得到答案。配合某些约束，一般可以在$O(n)或者 O(nlogn)$ 时间复杂度内解决问题。一般不超过$O(n^2)$。

【贪心算法】把集合分为【已处理集合】和【未处理集合】，贪心算法可以描述为“一直向前”，即在一定顺序下，对当前“局部”（一个（或者几个）元素，或者一颗子树）求【最优】，然后把这个元素放到【已解决】的集合，从而使得【未解决】的集合数目减少，这样循环或者递归求解即可。所以如果【假设】一个问题可以用【贪心】解决，则需要解决两个问题：

1. 按照什么【顺序】求解？一般要按照某个属性（或者属性的函数）进行排序。
2. 当前元素有多个满足条件的候选时，选择哪一个？

常见的贪心类型

【点】匹配【区间】问题

【输入】：区间集合$S=U_{i=1}^n \{l_i,r_i\}$，点集合 $T=\bigcup_{j=1}^m\{a_j\}$
【输出】：$max(\sum_{i\in S}\{l_i,r_i,a_i\}[l_i\le a_i \le r_i])$ （不完全）

含义是：区间和点一一匹配，最多有多少对？

• 【模型】找对象模型：每个人（【区间】）按自己“标准”（区间的L和R）找对象（点），怎样找是的整体“配”的对数最多？
• 【贪心思想】 尽量选“渣男”，把“帅哥”留给其他人。
• 【问题】以he？如何断定“渣男”还是“帅哥”？
  

  ---

【总体分析】
【区间】→【点】$s1\rightarrow t$
1. 如果区间 $s1$ 在点集合 $T$ 中没有匹配元素，则没有选择，$s1$对$Ans$贡献为$0$。
2. 如果区间 $s1$ 在点集合 $T$ 中只有一个点$t1$,则只能选择$t1$。 对$Ans$贡献为$1$。
3. 若区间 $s1$ 在点集合 $T$ 中有两个（或以上）点$t1，t2$, 任选一个，对$Ans$贡献为$1$，但会对剩余区间造成影响， 那么如何选择，才不会对剩余结果【变坏】？

所谓【变坏】，意思是：若有${s1}\rightarrow t1$，$s1\not \rightarrow t2$ ,
若有 $t1\rightarrow s2 \in (S-{s1})$，则必有，$s2\rightarrow t2$。

通俗一点的意思是：若$s1$【选择】的“渣男”$t1$ 都有别人$s2$要，则$s1$【放弃】的“帅哥”$t2$更能满足$s2$。$s1\rightarrow t1$并没有使得总体$Ans$变差。

问题是如何判断是“渣男”还是“帅哥”呢？
分析：从具体->抽象，从少到多，考虑两个区间两个点的情况：

尝试1：L从小到大排序：

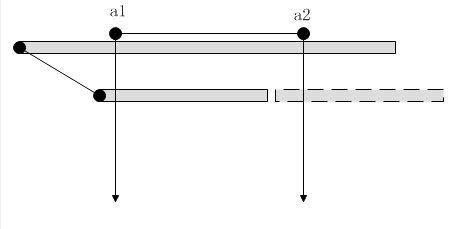
假设对于$[L1,R1]$有两个点 a1,a2均满足要求，由图中可见，无论选择a1,a2均无法【证明】剩余的点对$[L2,R2]$ 有必然影响。也就是说不存在【必然性】

尝试2：L从大到小排序：

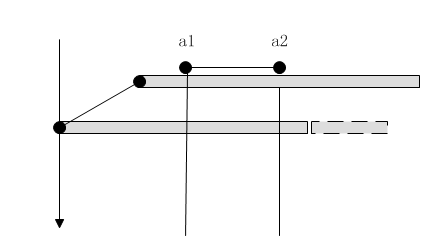
假设对于$[L1,R1]$有两个点 a1,a2均满足要求，由图中可见，若选择a2，则a1对$[L2,R2]$ 最优。原因是，$a_1 \in [L_2,a_2]$ ,当a2满足区间2的【匹配】时，a1必然匹配
（通俗说，若a2能被s2【兜住】，则a1必然必然能被s2【兜住】），$s1\rightarrow a2$，对【整体】$Ans$最优。

同理，可以尝试其他两种可能：

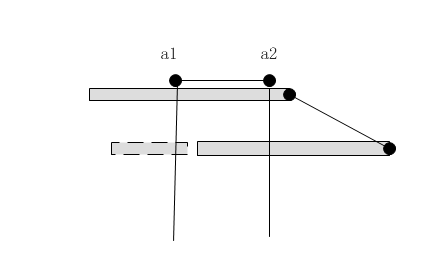
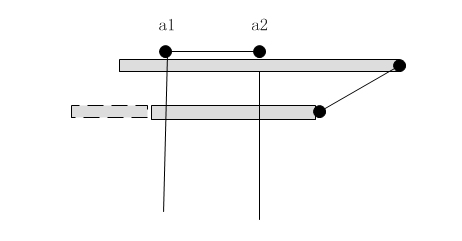
得出结论：当R 从小到大排列时，选择a1存在最优关系,(若a1能被【兜住】，则a2一定能被【兜住】)。

【结论】在区间和点的匹配问题中，当L从大到小排序时,或者R从小到大排序，存在一种选择比另外一种选择优，这种关系是通过【区间包含】来证明的。归纳为：【L从大到小排序】【选择距离排序端点最远的点】

此种情况下的贪心选择可以归纳为：
1. 区间按【L从大→小】或者【R 小→大】。
2.选择匹配点时，【选择距离排序端点最远的点】。

【证明】
1. 对于【当前区间】，因为对整体答案的贡献最大为1,若存在匹配的点，则选择【匹配】为最优。（贪心1）
2. 当选择了距离端点最远的点后，对于整体的最优性并没有变差（上面有了详细的说明）。